结构光之解相位求深度信息方法总结

结构光利用相位信息进行三维重建，主要包括解相位和展开相位，利用展开的相位计算深度信息。

 

解相位，也称为相位提取，主要包括相移法，傅里叶变换解相，卷积法解相。

（1）相移法

相移法主要是通过具有相移量的一组条纹图案来解相位，即需要已知有确定相位差的多幅光栅图像来获得相位，设

 为三个未知量，则需要最少三个已知相位的条纹图案来求解，所以对于相移法解相，也就是所说的三步相移，四步相移，五步相移等多步相移法。

多步相移法解相推导过程这里不再多说，可以参考以前的博文。

（2）傅里叶变换法解相

将正弦光栅投射到待测物体的三维表面，用照相机得到受被测物体深度调制的变形光栅条纹，对采集到的参考光栅像和变形光栅像的空间域信号分别进行傅立叶变换，在频域滤波得到基频分量，然后反傅立叶变换求得相位。

傅里叶变换法解相的推导过程也会在另一篇博文中介绍，这里只做介绍。

（3）卷积法

在光栅上选择合适的起始位置，得到光栅的数学表达式，然后通过将光栅信号与正余弦函数相乘，得到光栅中的低频分量，最后通过求解反正切函数的方法得到光栅的相位。推导过程同样见我的另一篇博文。

相移法是目前公认的最有效最可靠的方法，其实质是在时间轴上的逐点运算。由于采用多幅图像由光强得到的相位，计算量少，并且图像的阴影区容易分，具有一定的抗静态噪声能力。

 

相位展开

以上方法所提取的是相对相位，即相位主值，都是折叠相位，是被折叠在[-pi，pi]之间的，需要相位展开才能得到真实的相位。

从大的分类上说，主要有时间相位展开和空间相位展开。

相位展开的原理是：相邻两象素的相位主值进行比较，如果其相位差超出[-pi，pi]范围，则后面的象素加上或减去2pi，直到得到的相位是连续的。

由于空间相位展开法是不完全可靠的，且不能做到对所有情况有效，所以时间相位展开法为着重研究的展开方法。

时间相位展开法

时间相位展开法通过投射一系列不同频率的条纹图到被测物体表面，并同步拍摄得到一组受被测物体表面调制的而变形光栅条纹图，然后将每点的相位在这个序列上独立进行计算，从原理上避免了误差的传播。

Gray编码加相移算法与多频外差原理是使用最为广泛的两种时间相位展开算法。

 

深度信息求解

这里需要说明的是计算得到的相位值为绝对相位，对绝对相位值不同的处理方法有不同的深度信息计算方式。

在常见的双目视觉三维重建方法中，利用的是两个相机所拍摄到的图像特征点的匹配，然后利用三角测距的原理求的三维信息。

利用结构光技术的重建过程中，又分为两类，一类是有参考平面，一类是没有参考平面。

a: 有参考平面的系统中，只要求出参考平面和被测物体的相对相位差，利用PMP（相位测量轮廓法）方法即可求得深度信息。

 

 

 或者是这样的：

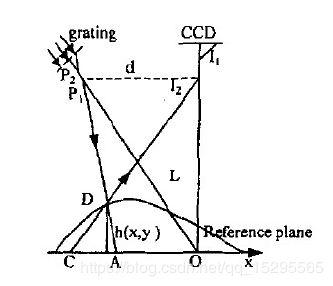
由投射系统投射正弦光栅，某光束P1 与参考平面交于 A 点。当放上物体后，由于受到了高度的调制，由 CCD 相机看到的该光束被移至到了 C 点。

这里A点和C点的相位差就是计算高度所需要的，那这两点在相机拍到的畸变条纹图像中是怎么体现的呢？

投射到参考平面的条纹图

 

被物体调制后的图像

这是所拍到的被调制前后的条纹图像，图中的红色点即相当于上图中的A点和C点，两点的像素坐标相同，相位不同，求的相同坐标下的相位差即可间接求的D点的高度。

 

针对这种求解方法，利用相移法提取相位在实现和推导的过程中有一些差别需要给出解释：

         投影仪投射的条纹图案是这样生成的：

         经过被测物体深度调制后相机采集到的图像是这样的：

         而在解相位的推导过程中是用的下面的式子：

 

b: 如果利用Gray编码加相移算法与多频外差原理展开得到的是像素点位置的绝对相位值，则利用下面的方法进行求解深度信息。

 一个 CCD 只可以确定一条空间直线，需要确定投影仪的灰度线平面，共同匹配出的点的三维坐标。采集的图像解相后，可根据 CCD 的绝对相位值可以求得投影仪对应的绝对相位值为：

up 为三维点在投影仪上的绝对相位值， ϕ 为三维坐标点在 CCD 中的绝对相位值， N 为光栅图像的条纹周期数， W 为投影仪在水平方向上的像素值。
被测物体上 A 点，对应于投影仪坐标系中的相位为u p 的直线。得知三维点在投影仪上的绝对相位值up 后，根据图像上的像素坐标到三维坐标的转化关系，可以求得绝对相位线对应的平面。 CCD 相机的像素点对应的直线和投影仪绝对相位对应的平面的交点，即为被测点的三维坐标。
 

思考：对于需要绝对相位的方法，是否需要减掉这一项呢？

如果有问题请在评论区留言，或者qq:857467352联系我。