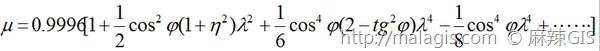常用地图投影

区域图投影

指除世界地图之外的半球图、大洲图、国家图、省区图、地区图,即含区域比较大的中小比例尺地图。

1. 圆锥投影
2. 方位投影
3. 伪圆锥投影

世界地图投影

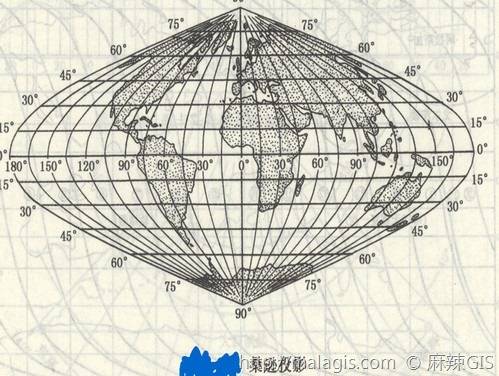
1. 多圆锥投影
2. 圆柱投影
3. 伪圆柱投影

地形图投影

1. 高斯－克吕格投影（简称高斯投影）
2. 等角圆锥投影
3. 通用横轴墨卡托投影

 

1.圆锥投影

基本概念

定义

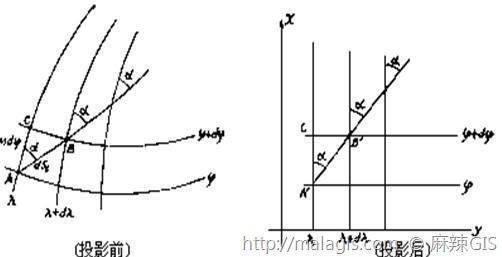
设想用一个圆锥套在地球椭球体上,而把地球椭球上经纬网投影到圆锥面上,然后沿着某一条母线(经线)将圆锥面切开而展成平面,就得到圆锥投影。圆锥面和地球椭球体相切称为切圆锥投影,圆锥面和地球椭球相割时称为割圆锥投影。

分类

按圆锥面与地球椭球体的相对位置分 :

正轴圆锥投影

圆锥轴与地球椭球体的旋转轴相一致；

横轴圆锥投影

圆锥轴与地球椭球体的长轴相一致；

斜轴圆锥投影

圆锥轴既不和椭球体的旋转轴重合， 也不与它的长轴相重合。

按变形性质分

等角圆锥投影

正轴等角圆锥投影也称为Lambert正形投影。

等面积圆锥投影

正轴等面积割圆锥投影也称为Albers投影。

任意投影

特例是等距离投影。

正轴圆锥的基本公式

极坐标公式为：

ρ=f(ϕ)ρ=f(ϕ)

δ=α⋅λδ=α⋅λ

其中δδ表示两条经线夹角在平面上的投影。

αα表示δδ与λλ的比值，小于1

λλ表示地球椭球体上两经线的夹角。

直角坐标公式为:

x=ρs−ρcosδx=ρs−ρcosδ

y=ρsinδy=ρsinδ

其中ρsρs表示制图区域最低纬线的投影半径

在该投影中,经纬线投影后呈正交，故a、b就是是m、n, 即经纬线方向就是主方向。

 

正等角圆锥投影

基本公式：

根据等角条件   a=b或 m=n，得：

dρ/(Mdϕ)=αρ/rdρ/(Mdϕ)=αρ/r

dρ/ρ=αMdϕ/(Ncosϕ)dρ/ρ=αMdϕ/(Ncosϕ)

将M，N 公式带入上式，并取积分可得：

ρ=K/Uαρ=K/Uα

K,αα称为投影常数

U=tg(450+ϕ/2)/tge(450+ψ/2)U=tg(450+ϕ/2)/tge(450+ψ/2)

sinψ=esinϕsinψ=esinϕ

当ϕ=00ϕ=00时，K=ρρ，故K的几何意义是赤道的投影半径

正等角圆锥投影的一般公式如下：

δ=α⋅λδ=α⋅λ

ρ=K/Uαρ=K/Uα

U=tg(450+ϕ/2)/tge(450+ψ/2)U=tg(450+ϕ/2)/tge(450+ψ/2)

sinψ=esinϕsinψ=esinϕ

e=((a2−b2)/a2)1/2e=((a2−b2)/a2)1/2

 

x=ρs−ρcosδx=ρs−ρcosδ

y=ρsinδy=ρsinδ

m=n=αρ/r=αK/(rUα)m=n=αρ/r=αK/(rUα)

p=m2=n2=(αK/(rUα))2p=m2=n2=(αK/(rUα))2

ω=0ω=0

 

投影常数αα,K的确定方法

1. 单标准纬线正等角圆锥投影:指定制图区域中某一条纬线无长度变形。
2. 双标准纬线正等角圆锥投影:指定制图区域中两条纬线无长度变形。
3. 定域等面积正等角圆锥投影:使制图区域各部分面积变形的总和为零，即制图区域总面积和原来的大小保持不变。

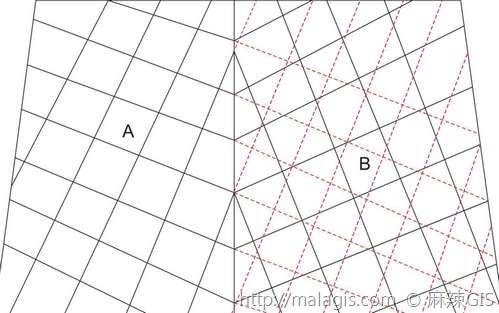
下图分别对应上述123

 

双标准纬线正等角圆锥投影

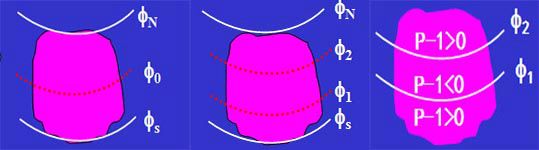
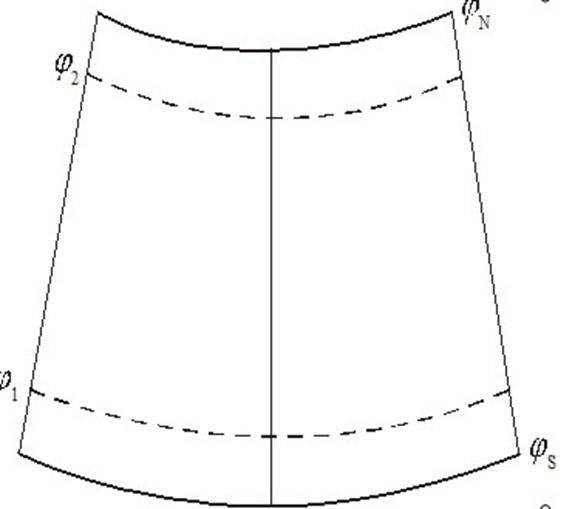
经纬线的表象：其经线表现为辐射的直线束,纬线投影成同心圆圆弧。圆锥面与椭球面相割的两条纬线圈，称为标准纬线（ϕ1,ϕ2ϕ1,ϕ2)。

标准纬线的位置：

ϕ1≈ϕs+35′ϕ1≈ϕs+35′

ϕ2≈ϕN−35′ϕ2≈ϕN−35′

ϕsϕs:制图区域最南边的纬度

ϕNϕN:制图区域最北边的纬度

双标准纬线正等角圆锥投影投影公式

α=(lgr2−lgr1)/(lgU1−lgU2)α=(lgr2−lgr1)/(lgU1−lgU2)

K=(r1Uα1)/α=(r2Uα2)/αK=(r1U1α)/α=(r2U2α)/α

其中：
U1=tg(450+ϕ1/2)/tge(450+ψ/2)U1=tg(450+ϕ1/2)/tge(450+ψ/2)

sinψ1=esinψ1sinψ1=esinψ1

其他的公式同前。

投影变形分析

1. 角度没有变形,即投影前后对应的图形保持相似,故也可称为正形投影;
2. 两条标准纬线上没有任何变形;
3. 等变形线和纬线一致,同一条纬线上的变形处处相等；
4. 在同一经线上,两标准纬线外侧为正变形(长度比>1)，而两标准纬线之
5. 为负变形(长度比<1),因此变形较均匀,绝对值也较小;

6. 同一纬线上等经差的线段长度相等,两条纬线间的经线线段长度处处相等。

我国的1:100万地图采用该投影,为了提高精度,1:100万地图的投影按百万之一地图的纬度划分原则—从赤道00开始，纬差40一幅，从南向北共分成15个投影带，每个投影带单独计算，建立数学基础。由于采用分带投影，每带纬度较小，我国范围内的1：100万地图变形值几乎相等，其长度变形最大不超过0.03%,面积变形约为长度变形的2倍。

圆锥投影的变形分析及应用

在切圆锥投影中，标准纬线ϕ0ϕ0处的长度比n0=1n0=1,其余纬线长度比均大于1，并向南、北方向增加；

在割圆锥投影中，标准纬线ϕ1ϕ2ϕ1ϕ2处长度比n1=n2=1n1=n2=1，变形自标准纬线ϕ1ϕ2ϕ1ϕ2向内和向外增大，在ϕ1ϕ1和ϕ2ϕ2之间n<1,在ϕ1ϕ1和ϕ2ϕ2以外n>1。

从变形特点，可得出结论：

圆锥投影最适用于中纬度处沿纬线伸展的制图区域。

2.方位投影

定义：

采用平面作为投影面，将地球椭球上的经纬网投影到该平面上，它也是圆锥投影的一种特例。

分类：

按投影面与地球相对位置的不同

正轴方位投影

地轴与投影平面垂直。

横轴方位投影

地轴与投影平面平行

斜轴方位投影

地轴与投影平面斜交。

按透视关系

非透视方位投影

等角方位投影、等面积方位投影、任意方位投影（特例：等距离方位投影）

透视方位投影

按视点位置不同分为：
正射方位投影：视点位于离球心无穷远处
外心方位投影：视点位于离球心有限距离处
球面方位投影：视点位于球面上
球心方位投影：视点与球心重叠一致

 

变形分析及其应用

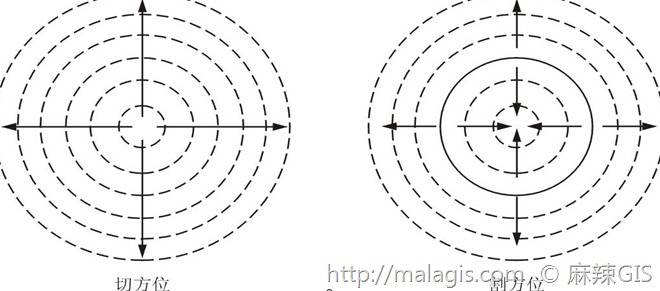
方位投影的等变形线呈圆形，即在正轴中与纬圈一致， 斜轴或横轴中与等高圈一致。

适用范围：最适宜于具有圆形轮廓的地区。

在两极地区，适宜用正轴方位投影。在赤道附近地区，适宜用横轴方位投影;其它地区用斜轴方位投影。

具体应用

等角方位投影

在欧州有些大比例尺地图的数学基础采用它；美国的UPS（Universal polar Stereographic)通用极球面投影，其实质是正轴等角割方位投影。

等面积方位投影

在小比例尺制图中，特别是东西半球图，应用得较多。

等距离方位投影

大多数世界地图集中的南北极图采用正轴等距离方位投影。

透视方位投影

球心投影：可用于编制航空图或航海图。
外心投影：在制作要求富有立体感的宣传鼓动图中应用较多。
正射投影：应用较少。

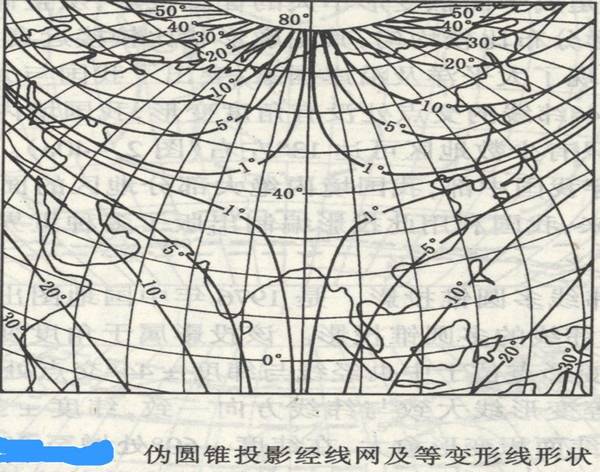
3.伪圆锥投影

伪圆锥投影定义：

是由法国彭纳（R.Bonne）于1752年设计的一种等积投影，故又称彭纳投影。

伪圆锥投影特点：

• 中央经线与中央纬线是没有变形的；
• 纬线形状仍然保持和圆锥投影一样的同心圆弧；
• 经线均投影成对称于中央经线的曲线；
• 该投影中，经纬线不正交。

 

伪圆锥投影应用：

常用于编制中纬地区小比例尺区域图，例如中国地图出版社出版的《世界地图集》中的亚洲政区图、英国《泰晤士地图集》中的澳大利亚与西太平洋地图。

4.多圆锥投影

多圆锥投影定义：

设想有许多圆锥与地球球面相切，并将球面的经纬网分别投影到这些圆锥面上，然后沿某一条母线将圆锥面剪开成平面，即得多圆锥投影。

描述

此投影的名称理解为“许多圆锥”。这是指其投影的方法。此方法对经线的形状产生影响。与其他圆锥投影不同，其中的经线是曲线而非直线。

投影方法

比常规圆锥投影复杂，但构造仍属简单。将无数个圆锥沿中央子午线对齐放置并进行投影后得到的即为此投影。此投影获得的纬线不是同心圆弧。每条纬线都表示相切圆锥的底部。

接触线

许多线；投影中的所有纬线。

线性经纬网

投影的中央子午线和赤道。

属性

形状

沿中央子午线的局部形状没有变形。变形随着距中央子午线距离的增加而增大；因此，东西方向的变形比南北方向的变形严重。

面积

面积的变形随着距中央子午线距离的增加而增大。

方向

沿中央子午线的局部角是准确的，其他位置的局部角则发生了变形。

距离

沿投影的纬线和中央子午线的比例是准确的。沿经线的变形随着距中央子午线距离的增加而增大。

局限性

在大比例尺地图中变形最小，例如地形地图方格，其中的经线和纬线在实际绘制中可以直线段表示。使用此类地图图幅生成地图库的方法并不可取，因为从多个方向连接各个地图图幅时，错误经过累积会显露出来。

用途和应用

用于从 1886 年到约 1957 年之间的 71/2 和 15 分的地形 USGS 四边形图幅。

此日期之后的一些新四边形图幅已经被错误地保存为多圆锥投影。东西方向美国国家平面坐标系的现有投影是兰勃特等角圆锥投影，而南北方向的美国区域投影是横轴墨卡托投影。

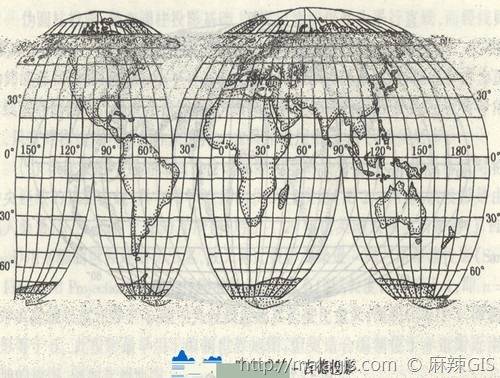
5.圆柱投影

圆柱投影基本概念：

根据特定的条件，将地球椭球面上的经纬线投影到圆柱面上，并沿圆柱母线切开展成平面，这种投影称为圆柱投影。

圆柱投影分类：

按变形性质分

等角圆柱投影,等面积圆柱投影和任意圆柱投影（特例：等距离圆柱投影)

按圆柱面与地球相对位置分

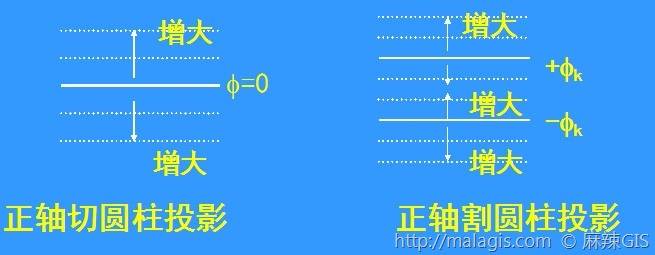
正圆柱投影
斜轴圆柱投影
横轴圆柱投影

正轴圆柱投影的一般公式

x=f(ϕ)x=f(ϕ)

y=α⋅λy=α⋅λ

m=dx/(Mdϕ)m=dx/(Mdϕ)

n=α/rn=α/r

p=a⋅b=m⋅n=αdx/(rMdϕ)p=a⋅b=m⋅n=αdx/(rMdϕ)

sinω/2=(a−b)/(a+b)=(m−n)/(m+n)sinω/2=(a−b)/(a+b)=(m−n)/(m+n)

或者：

tg(450+ω/4)=(a/b)1/2=(m/n)1/2tg(450+ω/4)=(a/b)1/2=(m/n)1/2

正轴等角圆柱投影（墨卡托投影）

公式：

x=α/modlgUx=α/modlgU

y=α⋅λy=α⋅λ

m=n=α/rm=n=α/r

p=m2p=m2

ω=0ω=0

其中mod=0.4342945

投影常数αα确定

令纬度ϕkϕk上的长度比nk=1nk=1

则

nk=a/rk=1nk=a/rk=1

α=rkα=rk

故

割圆柱投影中，α=rkα=rk

当ϕk=0ϕk=0时

切圆柱投影中，α=aα=a

等角航线（恒向线，斜向线）

是地面上两点之间的一条特殊的定位线，是两点间与所有经线处处成相同方位角的一条曲线。

等角航线在地图上的表象为两点之间的直线
tgα=(y2−y1)/(x2−x1)tgα=(y2−y1)/(x2−x1)

如图所示：

圆柱投影变形分析及其应用

适用范围：

低纬度处沿纬线延伸的地区。对于沿经线延伸的地区：采用横轴圆柱投影。

6.伪圆柱投影

伪圆柱投影概念：

伪圆柱投影是在圆柱投影基础上，规定纬线为平行直线，而经线则根据某些特定条件而设计成对称于中央经线的各类曲线（多为正弦曲线或椭圆曲线）的投影。

伪圆柱投影类型：

等积伪圆柱投影（应用最多）、任意伪圆柱投影

其中有代表性的如下：

• 桑逊投影：适合编制位于赤道附近南北延伸的地图，例如非洲地图、南美洲地图等。
• 摩尔威特投影:用于编制世界地图或东西半球图。
• 古德投影：美国古德(J.P.Goode)于1923年提出了一种分瓣伪圆柱投影方法来绘制世界地图。

桑逊投影

将纬线设计成间隔相等的平行直线，经线为对称于中央经线的正弦曲线，具有等积性质的伪圆柱投影。

摩尔威特投影

是一种等积性质的伪圆柱投影。

古德投影

将全制图区域根据需要，确定若干个中央经线位置，然后进行分瓣投影。

古德投影优点

每瓣中央经线两侧投影区域不至于过大，因此每瓣经线的弯曲度减少，变形也就减少。

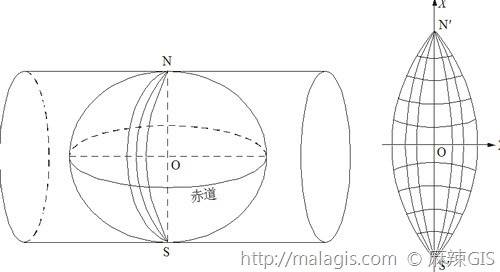
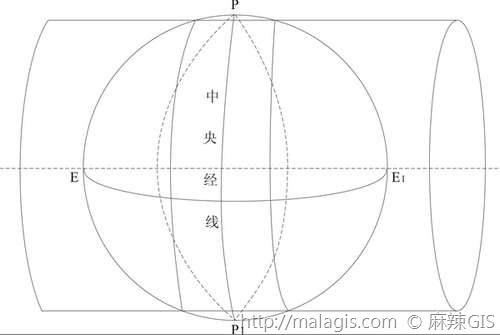
7.高斯－克吕格投影（简称高斯投影）

高斯－克吕格投影（简称高斯投影）的概念

从几何概念上分析，它是一种横轴等角切圆柱投影。我们把地球看成是地球椭球体，假想用一个椭圆筒横套在其上，使筒与地球椭球的某一经线（称为中央经线）相切，椭圆筒的中心轴位于赤道上，按等角条件将地球表面投影到椭圆筒上，然后将椭圆筒展开成平面。

 

高斯投影的基本条件

• 中央经线和赤道投影成垂直相交的直线
• 投影后没有角度变形，那么经纬线投影后仍正交
• 中央经线没有长度变形

投影的变形分析

其长度比的基本公式为：

μ=1+1/2cos2ϕ(1+η2)λ2+1/6cos4ϕ(2−tg2ϕ)λ4−1/8cos4ϕλ4μ=1+1/2cos2ϕ(1+η2)λ2+1/6cos4ϕ(2−tg2ϕ)λ4−1/8cos4ϕλ4

长度变形的规律是：

• 中央经线（λλ=0）上没有长度变形，即λλ=0，μμ=1
• 同一条纬线上，离中央经线越远变形越大，即λλ增大，μμ也增大
• 在同一经线上,纬度越低，变形越大，即ϕϕ越小，μμ越大

投影分带的规定

在1：2.5万到1：50万时，6060分带

在大于1：1万地形图中：3030分带

6060分带法

从格林尼治零度经线起,自东半球向西半球,每经差60分为一个投影带,即东经0～6,6～12,12～18,….174～180,用阿拉伯数字1,2,3,4….60表示投影带号,全球共分为60个投影带。

东半球中央经线的计算公式为:
L0=(6n−3)0L0=(6n−3)0

n表示投影带号，n<30

西半球中央经线的计算公式为:
L0=(6n−3)0−3600L0=(6n−3)0−3600

n表示投影带号，n>30

3030分带法

从东经1030′1030′ 算起，自东半球向西半球每3030为一带，将全球划分为120个投影带，1030′−4030′1030′−4030′ ,4030′−7030′4030′−7030′….其中央经线的位置为30,60,90,150…1800,−1770…−30,30,60,90,150…1800,−1770…−30,。

坐标网

经纬线网(又称为地理坐标网)

经线和纬线所构成的坐标网,它指示物体在地面上的地理位置。

方里网(直角坐标网)

平行于直角坐标轴的两组直线所构成的方里网格,每隔整公里绘出。在1：10万地形图上直接绘出。

1:5千～1:10万的地形图

经纬线只以图廓线的形式直接表现出来,并在图角处注出相应的度数,在内外图廓间还绘有加密经纬网的加密分划短线(称分度带)。

1:25万～1:100万的地形图

在图面上直接绘出经纬线网。
1:25万    △λ=15′△λ=15′  △ϕ=10′△ϕ=10′           
1:50万        30'      20' 
1:100万       1010       1010

方里网(直角坐标网)在≥1：10万的地形图上直接绘出 

我国地形图上方里网密度规定

比例尺     1:5千   1：1万   1：2.5万    1:5万      1:10万
图 上      20 cm    10cm      4cm        2cm        2cm                
实 地       1km      1km      1km        1km        2km

高斯-克吕格投影直角坐标网

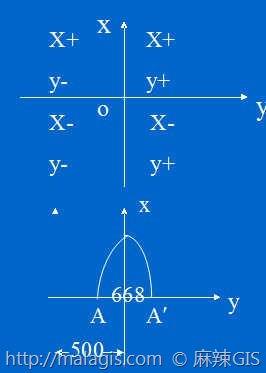
1.坐标系的建立

以每个投影带中央经线投影后的直线为X轴,赤道投影后的直线为y轴,其交点为原点。

为了保证y总是>0,将纵坐标轴向西平移500公里

图中A(-334,0),A'(334，0)移轴后,A点的坐标为(166,0), A'(834,0)

地图上所标出的x,y的值称为通用坐标

x = 3286330(m)         
y = 18 210420

在y坐标里18表示投影带号，210420表示实际坐标（加了500KM）

2.邻带方里网
为什么会产生邻带方里网？

 

原因：

高斯投影经线收敛于中央经线--相邻带两幅图拼接在一起使用时--两带图幅坐标网之间产生一折角--为了使用方便--在本带某一范围内加绘邻带方里网。

加绘规定

1:2.5万--1:10万

每个投影带西边缘经差30'范围,需加绘前一带的方里网。

每个投影带东边缘一列1:5万(15'),一列1:2.5万(7.5 ')内需加绘东带（后一带）方里网。

1：5000 、1:1万

投影带西边缘经差7.5',即两列1:1万,4列1:5000图上需要加绘邻带方里网。

地图上邻带方里网的表示方法

在外图廓线外绘一短线段

8.等角圆锥投影

 

9.通用横轴墨卡托投影

通用横轴墨卡托投影(UTM)概念：

从几何意义看，UTM投影属于横轴等角割圆柱投影，割点一般选在中央经线约±1˚40′。

 

基本公式：

直角坐标公式:

长度比公式:

投影变形分析及应用

1. 中央经线长度变形为-0.000 40
2. 两条割线上没有任何变形
3. 离这两条割线愈远则变形愈大。

该投影已被许多国家、地区和集团采用为地形图的数学基础，例如美国、日本、加拿大、泰国、阿富汉、巴西、法国、瑞士等约80个国家。