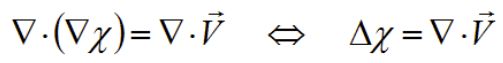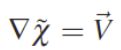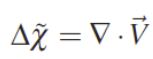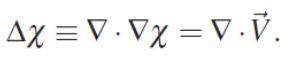初步认识泊松重建（比较全的综合教程）

整个算法的步骤包括对具有法向量信息的输入点云信息的预处理，对全局问题离散化，对离散化后的子数据求解，求解泊松问题后的等值面提取，以及后期优化处理等。
 表面重建过程：

1、定义八叉树。使用八叉树结构存储点集，根据采样点集的位置定义八叉树，然后细分八叉树使每个采样点都落在深度为D的叶节点；  

2、设置函数空间：对八叉树的每个节点设置空间函数F，所有节点函数F的线性和可以表示向量场V，基函数F采用了盒滤波的n维卷积；  

3、创建向量场：均匀采样的情况下，假设划分的块是常量，通过向量场V逼近指示函数的梯度。采用三次条样插值（三线插值）； 4、求解泊松方程：方程的解采用拉普拉斯矩阵迭代求出；

5、提取等值面：为得到重构表面，需要选择阈值获得等值面；先估计采样点的位置，然后用其平均值进行等值面提取，然后用移动立方体算法得到等值面。

泊松曲面重建基于泊松方程。泊松方程是一个比较常见的偏微分方程，在很多领域被应用，如高动态范围图像的调和映射、图像区域的无缝编辑、流体力学、网格编辑等, 多重网格泊松方法已应用于高效GPU计算。

由梯度关系得到采样点和指示函数的积分关系，根据积分关系利用划分块的方法获得点集的向量场，计算指示函数梯度场的逼近，构成泊松方程。根据泊松方程使用矩阵迭代求出近似解，采用移动立方体算法提取等值面，对所测数据点集重构出被测物体的模型，泊松方程在边界处的误差为零，因此得到的模型不存在假的表面框。采用隐函数的泊松方程进行表面重构是利用泊松方程在边界处没有误差的特点。
直接计算梯度场会引起向量场在表面边缘的无穷大值。因此首先用平滑滤波卷积指示函数，然后求平滑函数的梯度场。
高斯散度理论：平滑指示函数的梯度等于平滑表面法向场得到的向量场。
由于曲面未知，无法直接计算表面积分，把采样点集划分为小的区域块，通过对所有块的积分求和近似计算。知道向量场V后，可求指示函数。但向量场V不可积，使用最小平方逼近理论求解，应用散度算子得到泊松方程。
泊松表面重建一次性把所有的点都考虑在内，因此对噪声点有很好的弹性。泊松仿佛允许的层次结构支持局部的基函数，因此对稀疏线性系统的情况有很好的支持。在此基础上描述了多尺度的空间自适应算法，其时间和空间复杂度同重建模型的大小成正比。

 

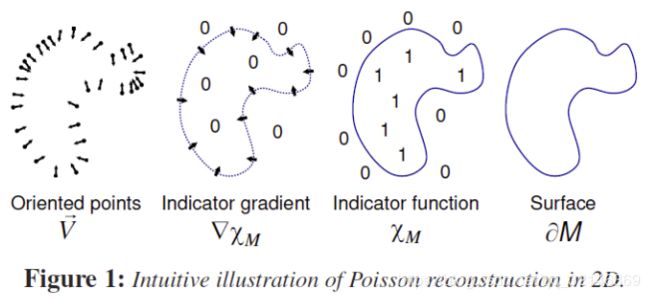
Poisson reconstruction的目的是生成watertight的且可以保有表面细节的重建方法。如果在空间中区分一个表面，我们可以直观的理解为表面外和表面内。Poisson重建就利用了这个关系，所以重建的关键在于indicator function，即指示函数。若一个元素属于这个集合则为1，否则为0，详细解释可以看百度百科或者维基百科。所以才有了论文中定义的在表面外为1，在表面内为0.如果这个时候我们对整个空间有效的指示函数进行梯度计算，我们会发现只有在接近物体表面的附近才有会有梯度向量，其余位置均为0向量。

此时所得到的表面附近梯度就正好等于了论文中所阐述的inner surface normal，也就是朝向表面内的法向量，-n（这个部分可以在维基百科中gradient词条里面找到更详细的解释和证明）。所以从这我们可以看出指示函数梯度场和输入采样点的法向量场是有一定联系的。此时想一下如果对一个采样数据集合进行重建，我们需要的输入数据具有什么属性？那么我们就能明确需要的是采样点的位置信息，还有采样点的法向量。那么如果构建指示函数和输入信息的关系呢？作者提出的方法是通过计算指示函数的散度（divergence），所以得到了如下的方程，来自paper

Implicit Function Fitting

为什么叫拟合法？这就不得不说到几何学中关于曲面表面的表达方式了。在一切几乎都可以用函数表达的几何学中，几何对象们都可以用函数表达，函数是定义域到值域的映射关系。而论文里又常见Equation–即方程这个词。方程是变量之间关系的等式。而隐函数，可以理解为满足了方程，而”隐藏”在方程中的函数关系。

隐式函数的图像，图像上的每个点都满足方程，但确不一定包含了满足方程的所有点。

举例：

改写为

就是满足方程的一个隐函数，而也满足。隐函数是一种对应关系，给了x，就有对应的y，而隐函数是可以显化的，比如(3)(4)把y提到左边的做法，就是隐函数的显化。隐函数是没有具体形式的，是隐藏在方程中的函数关系

为什么叫泊松重建？

回到正轨，传统的泊松重建就是在有向点云的基础上，空间中对于一个几何体表面(surface). 可以区分内外。比如泊松重建，它的效果是针对生成水密性的(watertight，我理解的就是封闭)的表面，所以就提出了一个指示函数(indicator function ), 注意下面这个图的下面那一堆Xm以及有倒三角的东西。。。利用这个指示函数的值来确定表里。

这个指示函数呢，是个分段函数。定义模型内部的值大于0，外部的值小于0，而为0的部分的等值面。提取出来就是几何目标模型的表面。

所以输入的点集是要有法向量的。说了半天，这个指示函数是怎么建立的呢？

数学预警分割线

---

有了具有法向的原始点集输入以后。就是我们要构建的指示函数。

作者先是推演了一下指示函数的梯度和法向向量场的积分关系，然后通过给定的数据点集积分求和计算这个曲面积分。最后把这个梯度场转化为求解泊松方程，进而构建的指示函数。

其实看到这我是有点懵逼的，你指示函数都没给我呢，我怎么来求梯度场？

先是关于梯度场的一些理论性证明：

因为这个指示函数是一个分段的常函数。所以在表面边界处精确计算梯度场时，向量场会算出无穷值。所以就可以先用一个平滑滤波器对指示函数进行卷积。来计算平滑后的函数的梯度场。为了证明这个合理性，就引理证明了一下平滑后的指示函数的梯度和曲面法向场的关系。

经过很多数学性的证明。可以证明出平滑后的指示函数的梯度，和通过曲面法线场算的的向量场相等。

怎么估计这个向量呢？

现在只有点集，连曲面表面都没有啊，所以曲面积分是算不出来的，我们只有有向点集。但是作者用离散求和近似的方式去计算曲面积分。这样就算出的向量场。还记得前面的证明结论么，平滑指示函数的梯度等于平滑后表面法向场得到的向量场。

所以知道向量场后，就可以求指示函数了。

但是向量场是不可积的。所以没有精确解，只能近似，利用最小二乘估计，又引入散度算子组成泊松方程。

而求解泊松方程的过程，就找到了这个指示函数。

好了我们来总结一下：

泊松重建的关键是找到一个指示函数。指示函数的值确定了待重建目标的表里，通过求解这个指示函数找到函数值相同点，并提取出一个等值面，进而实现了重建。

作者有一个预设，且有一系列数学的证明，证明了指示函数的梯度等于结合表面法线场计算得到的向量场。这也是高斯散度理论。(理论如此，实际是求近似)

倒三角是梯度.但是，指示函数不知道，梯度不知道。

只能计算出向量场。所以应用散度算子这一媒介。转化成了一个泊松方程。

这个三角又变成正三角了？
 两个三角会看着很迷惑，这是很多人学习后从入门到放弃的很大原因之一。再强调一下！其中：

是我们想要的函数，我们希望解出它来。
 这个正三角，就是梯度的散度(也是拉普拉斯算子)  (正三角表示拉普拉斯算子–梯度的散度)。也就是

梯度的散度等于向量场的散度。

解这个泊松方程就能找到指示函数。方程的解采用拉普拉斯矩阵迭代求出 。
 而后利用等值面提取。提取方法则是通过Marching Cube方法，但那就是另一篇文章了。

特点 支持噪声和非均匀的数据 有时会平滑过渡 解算时间超线性(super-linea :也就是数据量越大，解算时间会更久)