论文笔记 - Cross-dimensionalWeighting for Aggregated Deep Convolutional Features

abstract

本文主要提出了一种直接有效的图像表示方法，是通过交叉维度的赋权以及对深层卷积神经网络层输出进行聚合（cross-dimensional weighting and aggregation of deep convolutional neural network layer outputs.）
首先介绍了一些通用的框架，包含了一系列的方法以及交叉维度的pooling和赋权步骤，然后提出一个非参数的模式进行 spatial-wise 和 channel-wise 赋权。

Introduction

神经网络在图像搜索应用中效果很好，它能够提取较为深层、抽象的特征。很多的图像搜索方法都基于深度特征（deep features）。Babenko et al. and Razavian et al. 提出不同的 pooling 方法对deep features 池化，将图像表示为几百维度的 compact 向量表示。
根据这些只是，本文提出一种简单、直接的方式来构建图像特征表示，方法是通过 交叉维度的赋权以及聚合（via cross-dimension weighting and aggregation）
本文的提取特征的方法基于深度卷积神经网络，因为我们是对全连接层之前的那些卷积层的输出进行聚合，所以每层的维度会不同（因为神经元的个数不同）。所谓本文没有对输入图像进行resizing和cropping操作，使得不同长宽比 aspect ratios 的图像能够保留内部的空间特性。
在对CNN的最后一层提取深度卷积特征之后，对每个空间位置 spatial 以及每个管道 channel 赋权，最后通过 sum-pooling 得到最终的聚合结果，也就是图像的特征 feature。
总结一下：

• 提出了一种对卷积特征进行聚合 aggregation 的框架，包括 cross-dimensional weighting and pooling steps 赋权和池化
• 提出一种非参数化的赋权模式进行 spatial- and channel-wise weighting，这种赋权能够 boost the effect of highly active spatial responses and regulate the effect of channel burstiness respectively
• 在三个public的数据集上 for image search 进行了验证，without any fine-tuning

效果：使用 mean average precision 作为标准，本方法比之前最好的方法要高 10%

Related work

很多的图像搜索方法都是 bag-of-words 模型的变种，都是基于局部特征，代表性的是SIFT，还有一些对BOW模型的扩展，比如 soft assignment [27], spatial matching [2, 26], query expansion [1, 6, 7, 35], better descriptor normalization [1], feature election [36, 38], feature burstiness [15] and very large vocabularies [22]，这些方法很难扩展规模，因为每个图像是用上百个patch表示，时间上和存储上受限。
接着，研究转向了全局图像表示，代表性的包括 VLAD 和 Fisher Vectors。

Framework for Aggregation of Convolutional Features

Framework Overview

• 1: Perform spatially-local pooling，首先使用 Sum-pooling or max-pooling 对每个通道内的局部空间近邻进行池化，with neighborhood size w×h w × h and stride s.
• 2: Compute spatial weighting factors.对每个通道的每个 (i,j) ( i , j ) 位置 赋权 αij α i j
• 3: Compute channel weighting factors. 对每个通道 k 中的每个位置赋权 βk β k
• 4: Perform weighted-sum aggregation. 对每个通道中的元素求和，聚合成一个向量。
  fk=∑i=1W∑j=1HX′kij f k = ∑ i = 1 W ∑ j = 1 H X k i j ′
• 5: Perform vector normalization. 对得到的向量进行 normalized and power-transformed 范化和转换，这个步骤可以使用很多的 norms，比如 L1, L2, infinite
• 6: Perform dimensionality reduction. 对范数化之后的向量降低维度，使用PCA和白化
• 7: Perform final normalization. 最后再次进行范数化
  

Cross-dimensional Weighting

用 X∈RK×W×H X ∈ R K × W × H 表示3-dimensional 特征向量。 K K 表示通道数， W,H W , H 表示空间维度。
用 X′ X ′ 表示赋权之后的特征张量，per-location weights αij α i j , per-channel weights, βk β k :

Xkij=C(k)ij=λijk X k i j = C i j ( k ) = λ k i j

X′=αijβkXkij X ′ = α i j β k X k i j

然后使用 sum-pooling per channel 对得到赋权特征张量进行聚合 F={f1,...,fk} F = { f 1 , . . . , f k }

fk=∑i=1W∑j=1HX′kij f k = ∑ i = 1 W ∑ j = 1 H X k i j ′

聚合之后，使用L2-norm 对 F F 范化，然后使用PCA、whiten 降维，最后再进行 L2-norm，得到 CroW 特征

Feature Weighting Schemes

非参数化的 spatial and channel weighting，没有使用到额外的参数，主要是根据了原始的输入信息。

Response Aggregation for Spatial Weighting αij α i j

Spatial Weighting：based on the normalized total response across all channels.基于范数化之后(因为算法的第一步是进行 max- or sum-pooling)的所有通道的response总和。 S′∈RW×H S ′ ∈ R W × H 表示所有通道的每个空间位置 (i,j) ( i , j ) 的聚合反应

S′=∑kCk S ′ = ∑ k C k

得到 aggregated spatial response map S S

Sij=(S′ij(∑m,n(S′mn)a)1/a)1/b S i j = ( S i j ′ ( ∑ m , n ( S m n ′ ) a ) 1 / a ) 1 / b

setting αij=Sij α i j = S i j 得到空间权重因子

在实验中，使用了 L1, L2, inf 范数，当 a=0.5 a = 0.5 的时候结果相差不大，所有本文选择了 L2, b=2 b = 2 。

无参数化的原因：根据算法第一步得到的映射，得到了 Ck C k ,从而得到了 S′ S ′ ， 最终得到了 S S ，并没有引入其他的参数。

（下面的图没有看懂）

Sparsity Sensitive Channel Weighting（稀疏敏感通道赋权）

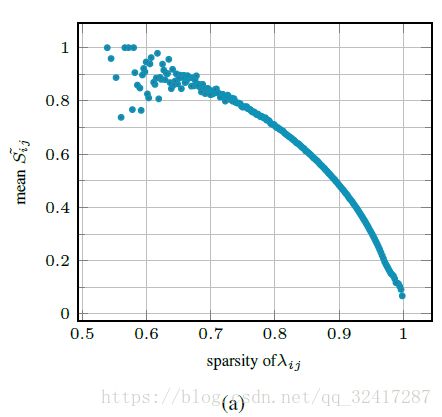
channel weighting: 基于特征映射feature map 的稀疏性 sparsity。我们想达到的效果是对于给定的特征在相似的图像中出现的频率应该近似。

定义：非零元素出现的比例： Qk Q k for each channel k k ，得到每个通道的稀疏性：

Ξ=1−Qk Ξ = 1 − Q k

其中 Q=1WH∑ij[λ(ij)>0] Q = 1 W H ∑ i j [ λ ( i j ) > 0 ]

λ(ij) λ ( i j ) 代表的是空间位置 (i,j) ( i , j ) 的所有通道 λ(ij)k λ k ( i j )

所以 Ξ∈RK Ξ ∈ R K

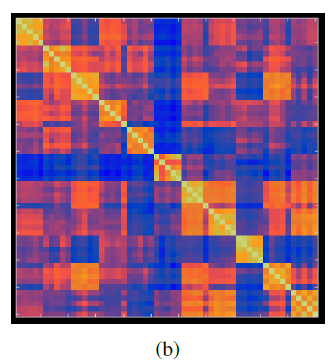
图像是在 Paris 数据集上做的实验，其上共11个类，每个类有5张图像。从图（b）上可以看出 对角线上一共11个方块，代表相同的landmark相似度高，其他代表不同的landmark相似度没那么高

在我们得到聚合的特征的时候，对每个 （i， j）位置上的所有的通道进行了 sum-pool 操作，这就使得那些有特征出现次数比较多的通多激活的程度更大，【channels with frequent feature occurrences are already strongly activated in the aggregate feature】但是对于那些特征比较少的通道，进行sum之后，可能激活程度没那么大，但是传递的信息更多。类似于TF-IDF，越少的内容信息量越大。 inverse document frequency 所以对较少特征的贡献进行方法，通过对其所在的那个通道增加权重 Ik I k

Ik=log(Kϵ+∑hQhϵ+Qk) I k = l o g ( K ϵ + ∑ h Q h ϵ + Q k )

∑hQh ∑ h Q h 经过 sum-pool 之后就固定了， ϵ ϵ 是一个较小的常数保证数值的稳定性。 Qk Q k 越小，得到的信息量越大。

所以本节的内容是 * 稀疏敏感通道赋值*
(Our sparsity sensitive channel weighting is also related to and motivated by the
notion of intra-image visual burstiness) 与图像内部的可视突出的概念相关。【什么意思】稀疏性较差的通道对应于那些在很多图像区域提供非零项的 filters
【】

Discussion

可以使用不同的方法进行 pooling, weighting, aggregation.

Uniform weighting.

设置 spatial 和 channel 权重相等，然后对每个通道执行 sum-pooling 操作，得到一个简单的Crow版本，叫做 uniform Crow 或者 uCrow。

这个相同权重，在代码实现上是没有加上权重，等价于 non-weighting

Relation to SPoC features

SPoC: refer to Babenko, A., Lempitsky, V.: Aggregating deep convolutional features for image retrieval. ICCV (2015)

CroW 和SPoC 区别 在于 spatial pooling, spatial weighting, and channel weighting。

• spatial pooling：CroW 使用的深度卷积网络的最后一个池化层的输出，SPoC使用的是最后一个卷积层的输出。
• spatial weighting：SPoC在spatial weighting时，首先使用了中心化操作【centering】，CroW则从当层输出的空间激励项spatial activations得到spatial weighting。[无参数]
• channel weighting：SPoC使用的是 uniform channel weighting，CroW使用的是从通道稀疏中得到 channel weighting。[无参数]

Experiments

Evaluation Protocol

• Datasets for image search
  
  • Oxford - use cropped queries 作为CNN的输入并通过这些切片提取特征
  • Paris
  • Oxford100k as distractors 干扰项
  • Holidays - use the ‘upright’ version of the images
• Evaluation Metrics 评价准则
  
  • mean average precision (mAP)
  • Caffe
  • pre-trained VGG16 model
  • 【zero-center the input image by mean pixel subtraction】
• Query Expansion
  
  • at the cost of one extra query.
  • 根据待查询图像给定一个升序排列的数据集合，可得聚合特征，然后重新进行查询 re-query

Preliminary Experiments 预实验

• Image size and layer selection
  
  • SPoC using VGG19, uCroW using VGG16，网络较小，但是效果更好
  • uCroW保持输入图像的原始大小
  • 采用池化层比采用卷积层效果要好
    
• Effect of the final feature dimensionality
  
  • CroW using the sparsity sensitive channel weighting 受维度的影响较大，可以被解释为 后续的降维操作对其影响更大。当计算稀疏敏感权重的时候使用到了所有的维度，经过降维之后，很多的维度被丢弃了discarded。

• Notes on max-pooling
  
  • 当使用了白化之后，max-pooling 效果不如 sum-pooling
• Whitening.
  
  • （as dimensions are reduced, more dimensions that are selective for buildings are kept when we learn the reduction parameters on a semantically similar dataset like Oxford.）【不太懂】

Image Search

• (CroW improves performance in all cases, with the gain increasing as the dimensionality of the final features decreases.）【CroW在所有情况下都能提高性能，随着最终的特征维数减少，增益也会增加】
• 使用查询扩张 (query expansion) 之后，可以得到更好的结果。the top ranked results are already of high quality.

Conclusions

• 提出了一个聚合卷积特征的一般性框架，使用了交叉维度赋权 cross-dimensional weighting
• 提出了一种简单的、非参数化的赋权模式：spatial- and channel-wise weighting
• 值得研究的参数赋权方式

---

refer:

• Cross-dimensional Weighting (CroW) aggregation
• Code