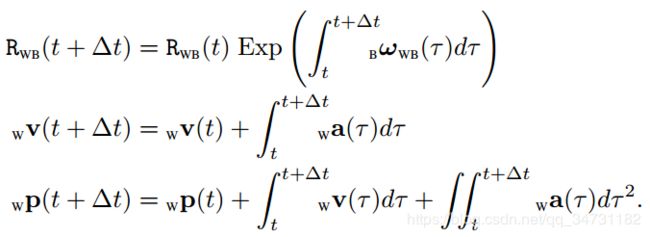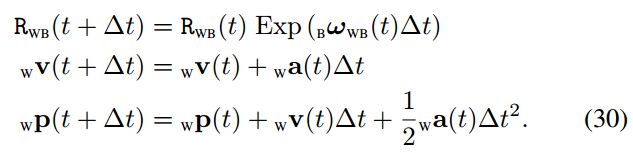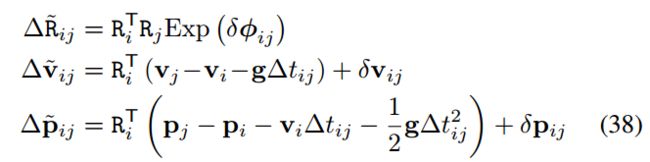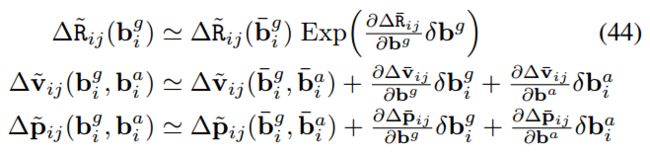IMU预积分公式汇总
本文中全部公式来自论文:On-Manifold Preintegration for Real-Time Visual-Inertial Odometry
为了查看公式时更加方便,现把文中的有关IMU预积分的公式汇总如下:
IMU观测模型
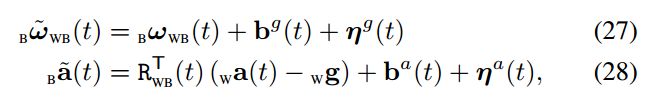
B ω ~ W B ( t ) _{\mathrm{B}} \tilde{\omega}_{\mathrm{WB}}(t) Bω~WB(t)是陀螺仪观测值, B a ~ ( t ) _{\mathbf{B}} \tilde{\mathbf{a}}(t) Ba~(t)是加速度计观测值, w g _\mathrm{w} \mathrm{g} wg是重力加速度, b g ( t ) \mathbf{b}^{g}(t) bg(t)和 b a ( t ) \mathbf{b}^{a}(t) ba(t)分别是陀螺仪和加速度计的零偏, η g ( t ) \boldsymbol{\eta}^{g}(t) ηg(t)和 η g ( t ) \boldsymbol{\eta}^{g}(t) ηg(t)分别是陀螺仪和加速度计的观测噪声。
IMU预积分模型
带入IMU观测模型后:

考虑两个关键帧之间的IMU预积分:

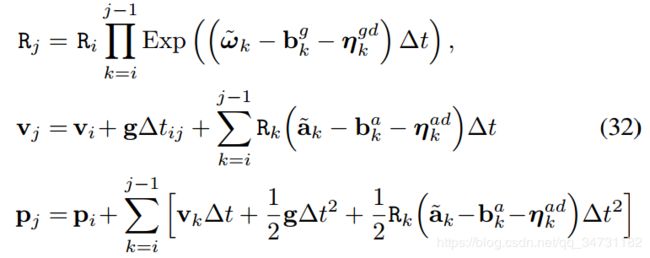
将上式转换为两帧之间的相对运动关系(包括相对旋转、速度和位置):

假设两个关键帧之间的陀螺仪和加速度计的零偏保持恒定:

状态噪声向量为: [ δ ϕ i j ⊤ , δ v i j ⊤ , δ p i j ⊤ ] ⊤ [\delta \phi_{i j}^{\top}, \delta \mathbf{v}_{i j}^{\top}, \delta \mathbf{p}_{i j}^{\top} ]^{\top} [δϕij⊤,δvij⊤,δpij⊤]⊤
计算协方差阵
迭代求解状态噪声:
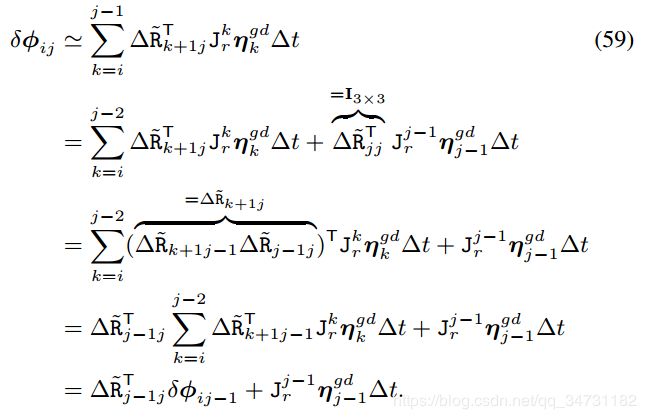
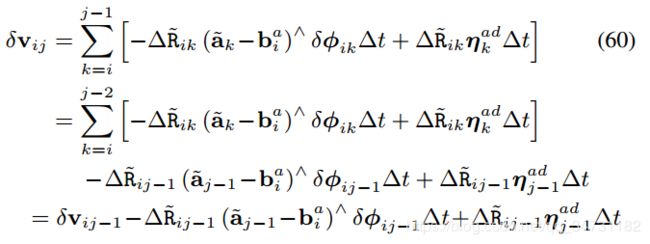

通过噪声向量构建协方差阵:
η i k Δ ≐ [ δ ϕ i k , δ v i k , δ p i k ] η k d ≐ [ η k g d η k a d ] \boldsymbol{\eta}_{i k}^{\Delta} \doteq\left[\delta \boldsymbol{\phi}_{i k}, \delta \mathbf{v}_{i k}, \delta \mathbf{p}_{i k}\right]\\ \boldsymbol{\eta}_{k}^{d} \doteq \left[ \begin{array}{ll}{\boldsymbol{\eta}_{k}^{g d}} & {\boldsymbol{\eta}_{k}^{a d}}\end{array}\right] ηikΔ≐[δϕik,δvik,δpik]ηkd≐[ηkgdηkad]
其中, η i k Δ \boldsymbol{\eta}_{i k}^{\Delta} ηikΔ为状态噪声, η k d \boldsymbol{\eta}_{k}^{d} ηkd为IMU观测噪声
将式(59)-(61)写为矩阵形式:
η i j Δ = A j − 1 η i j − 1 Δ + B j − 1 η j − 1 d \boldsymbol{\eta}_{i j}^{\Delta}=\mathbf{A}_{j-1} \boldsymbol{\eta}_{i j-1}^{\Delta}+\mathbf{B}_{j-1} \boldsymbol{\eta}_{j-1}^{d} ηijΔ=Aj−1ηij−1Δ+Bj−1ηj−1d
则协方差阵为:
Σ i j = A j − 1 Σ i j − 1 A j − 1 ⊤ + B j − 1 Σ η B j − 1 ⊤ \boldsymbol{\Sigma}_{i j}=\mathbf{A}_{j-1} \boldsymbol{\Sigma}_{i j-1} \mathbf{A}_{j-1}^{\top}+\mathbf{B}_{j-1} \boldsymbol{\Sigma}_{\eta} \mathbf{B}_{j-1}^{\top} Σij=Aj−1Σij−1Aj−1⊤+Bj−1ΣηBj−1⊤
融合零偏更新
实际上,两个关键帧之间的陀螺仪和加速度计的零偏已经发生了变化 δ b \delta \mathrm{b} δb,在 j j j时刻的零偏应该等于 b = b ‾ + δ b \mathrm{b}=\overline{\mathrm{b}}+\delta \mathrm{b} b=b+δb
计算残差雅可比
相关参数: δ ϕ i , δ p i , δ v i , δ ϕ j , δ p j , δ v j , δ ~ b i g , δ ~ b i a \delta \boldsymbol{\phi}_{i}, \delta \mathbf{p}_{i}, \delta \mathbf{v}_{i}, \delta \boldsymbol{\phi}_{j}, \delta \mathbf{p}_{j}, \delta \mathbf{v}_{j}, \tilde{\delta} \mathbf{b}_{i}^{g}, \tilde{\delta} \mathbf{b}_{i}^{a} δϕi,δpi,δvi,δϕj,δpj,δvj,δ~big,δ~bia