数据结构实现 7.1:线段树(C++版)
数据结构实现 7.1:线段树(C++版)
- 1. 概念及基本框架
- 2. 基本操作程序实现
- 2.1 构建操作
- 2.2 查找操作
- 2.3 其他操作
- 3. 算法复杂度分析
- 3.1 构建操作
- 3.2 查找操作
- 4. 完整代码
1. 概念及基本框架
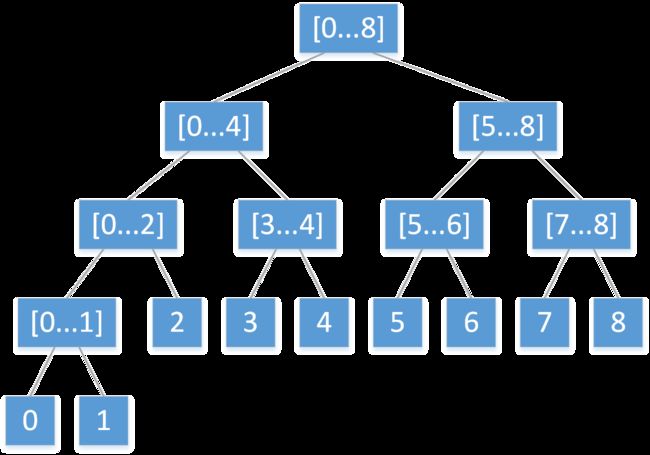
线段树 是一种二叉树,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
如上图中,每个结点可以存一些这个区间内的元素的性质,比如:和、最大值、最小值……通过不同区间的组合,我们可以访问到特定的区间元素的性质。因为划分区间我们采用二分的方法,而且左边的元素数目大于等于右边的元素数目,所以线段树本质上也是一棵完全二叉树。
注:这里线段树的每个结点存的只是一个元素,即这个区间元素的性质。
这里给出线段树大体框架:
template <class T>
class SegmentTree{
public:
SegmentTree(T *arr, int len){
m_data = new T[len];
for (int i = 0; i < len; ++i){
m_data[i] = arr[i];
}
m_size = len;
m_tree = new T[4 * len];
m_treeSize = 0;
buildSegmentTree(0, 0, m_size - 1);
}
...
private:
T *m_data;
int m_size;
T *m_tree;
int m_treeSize;
MergerNew<T> m;
};
m_data 用来接收线段树中原来的 n 个元素。
m_size 表示线段树的原数据大小。
m_tree 用来存储线段树每个结点的数据。
m_treeSize 表示线段树结点的数目。
m 可以认为内部有一个函数包可供我们调用,后面会详细讲述。
同样,为了保护数据,这些变量都放在 private 区。
buildSegmentTree 是一个线段树的构建函数,下面会详细讲述。
注:构造函数中,我们发现线段树结点提供了 4n 个,这是为了防止越界。
接下来我们就对线段树的构建、查询以及一些其他基本操作用代码去实现。
2. 基本操作程序实现
2.1 构建操作
为了不断划分区间,我们需要的到完全二叉树中,一个结点左右子结点的索引,这一点很类似于 6.1 中 最大二叉堆 的做法。原理不再赘述,给出其实现函数:
template <class T>
class SegmentTree{
...
private:
//返回完全二叉树中,一个结点左子结点的索引
int leftChild(const int index) const {
return 2 * index + 1;
}
//返回完全二叉树中,一个结点右子结点的索引
int rightChild(const int index) const {
return 2 * (index + 1);
}
...
};
有了索引,我们就可以不断地进行区间划分,进而构建出一棵线段树。构建的实现函数如下:
template <class T>
class SegmentTree{
...
private:
...
//在treeIndex位置创建表示区间[left...right]的线段树
void buildSegmentTree(const int treeIndex,const int left,const int right){
m_treeSize++;
if (left == right){
m_tree[treeIndex] = m_data[left];
return;
}
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
int mid = (left + right) / 2;
buildSegmentTree(leftTreeIndex, left, mid);
buildSegmentTree(rightTreeIndex, mid + 1, right);
//以求和为例
m_tree[treeIndex] = m.merger(m_tree[leftTreeIndex], m_tree[rightTreeIndex]);
}
...
};
这里利用的是二分的思想,不断划分区间,直到区间只有一个元素时停止。
为了能够不只是用来求和,我特意构建了一个类用来自定义需要的函数,即 MergerNew 类,这个类的实现代码如下:
template <class T>
class MergerNew : Merger<T>{
public:
T merger(T a, T b){
return a + b;
}
};
这里我们可以自定义实现函数,完成线段树区间不同性质的构建。
这里是在虚函数接口上实现的类,虚函数如下:
template < class T>
class Merger{
public:
virtual T merger(T a, T b) = 0;
};
2.2 查找操作
这里我们提供两个查询函数,get 和 query ,函数实现代码如下。
template <class T>
class SegmentTree{
public:
...
T get(const int index) const{
if (index < 0 || index >= m_size){
cout << "访问越界!"
throw 0;
}
return m_data[index];
}
T query(const int queryL, const int queryR) {
if (queryL < 0 || queryL >= m_size || queryR < 0 || queryR >= m_size){
cout << "访问越界!" << endl;
throw 0;
}
return query(0, 0, m_size - 1, queryL, queryR);
}
private:
...
T query(const int treeIndex,const int left,const int right,const int queryL,const int queryR) {
if (left == queryL && right == queryR){
return m_tree[treeIndex];
}
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
int mid = (left + right) / 2;
if (queryL >= mid + 1){
return query(rightTreeIndex, mid + 1, right, queryL, queryR);
}
else if (queryR <= mid){
return query(leftTreeIndex, left, mid, queryL, queryR);
}
T leftRes = query(leftTreeIndex, left, mid, queryL, mid);
T rightRes = query(rightTreeIndex, mid + 1, right, mid + 1, queryR);
return m.merger(leftRes, rightRes);
}
...
};
get 用于查找原数据。
query 用于某区间元素性质查询。同样,这里采用了二分法的思想。
2.3 其他操作
线段树还有一些其他的操作,包括 线段树大小 等的查询操作。
template <class T>
class SegmentTree{
public:
...
int size() const {
return m_treeSize;
}
bool isEmpty()const{
return m_treeSize== 0;
}
void print() const {
cout << "SegmentTree: " << "Size = " << m_treeSize << endl;
cout << '[';
for (int i = 0; i < m_treeSize; ++i){
cout << m_tree[i];
if (i != m_treeSize - 1){
cout << ',';
}
}
cout << ']' << endl;
}
...
};
3. 算法复杂度分析
3.1 构建操作
| 函数 | 最坏复杂度 | 平均复杂度 |
|---|---|---|
| add | O(nlogn) | O(nlogn) |
一共有 n 个元素,每个元素要从线段树根到线段树的叶子才能完成线段树的构建,所以每个元素的时间复杂度是 logn ,总的时间复杂度是 nlogn。
3.2 查找操作
| 函数 | 最坏复杂度 | 平均复杂度 |
|---|---|---|
| get | O(1) | O(1) |
| query | O(logn) | O(logn) |
总体情况:
| 操作 | 时间复杂度 |
|---|---|
| 建 | O(nlogn) |
| 查 | O(logn) |
4. 完整代码
程序完整代码(这里使用了头文件的形式来实现类)如下:
虚函数接口 代码如下:
#ifndef __MERGER_H__
#define __MERGER_H__
template < class T>
class Merger{
public:
virtual T merger(T a, T b) = 0;
};
#endif
线段树 类代码:
#ifndef __SEGMENTTREE_H__
#define __SEGMENTTREE_H__
#include "Merger.h"
template <class T>
class MergerNew : Merger<T>{
public:
T merger(T a, T b){
return a + b;
}
};
template <class T>
class SegmentTree{
public:
SegmentTree(T *arr, int len){
m_data = new T[len];
for (int i = 0; i < len; ++i){
m_data[i] = arr[i];
}
m_size = len;
m_tree = new T[4 * len];
m_treeSize = 0;
buildSegmentTree(0, 0, m_size - 1);
}
int size() const {
return m_treeSize;
}
bool isEmpty()const{
return m_treeSize == 0;
}
void print() const {
cout << "SegmentTree: " << "Size = " << m_treeSize << endl;
cout << '[';
for (int i = 0; i < m_treeSize; ++i){
cout << m_tree[i];
if (i != m_treeSize - 1){
cout << ',';
}
}
cout << ']' << endl;
}
T get(const int index) const{
if (index < 0 || index >= m_size){
cout << "访问越界!"
throw 0;
}
return m_data[index];
}
T query(const int queryL, const int queryR) {
if (queryL < 0 || queryL >= m_size || queryR < 0 || queryR >= m_size){
cout << "访问越界!" << endl;
throw 0;
}
return query(0, 0, m_size - 1, queryL, queryR);
}
private:
//返回完全二叉树中,一个结点左子结点的索引
int leftChild(const int index) const {
return 2 * index + 1;
}
//返回完全二叉树中,一个结点右子结点的索引
int rightChild(const int index) const {
return 2 * (index + 1);
}
//在treeIndex位置创建表示区间[left...right]的线段树
void buildSegmentTree(const int treeIndex,const int left,const int right){
m_treeSize++;
if (left == right){
m_tree[treeIndex] = m_data[left];
return;
}
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
int mid = (left + right) / 2;
buildSegmentTree(leftTreeIndex, left, mid);
buildSegmentTree(rightTreeIndex, mid + 1, right);
//以求和为例
m_tree[treeIndex] = m.merger(m_tree[leftTreeIndex], m_tree[rightTreeIndex]);
}
T query(const int treeIndex,const int left,const int right,const int queryL,const int queryR) {
if (left == queryL && right == queryR){
return m_tree[treeIndex];
}
int leftTreeIndex = leftChild(treeIndex);
int rightTreeIndex = rightChild(treeIndex);
int mid = (left + right) / 2;
if (queryL >= mid + 1){
return query(rightTreeIndex, mid + 1, right, queryL, queryR);
}
else if (queryR <= mid){
return query(leftTreeIndex, left, mid, queryL, queryR);
}
T leftRes = query(leftTreeIndex, left, mid, queryL, mid);
T rightRes = query(rightTreeIndex, mid + 1, right, mid + 1, queryR);
return m.merger(leftRes, rightRes);
}
private:
T *m_data;
int m_size;
T *m_tree;
int m_treeSize;
MergerNew<T> m;
};
#endif