复杂网络多局域世界模型matlab算法实现

3.12.1 多局域世界模型的构造方法

多局域世界模型主要是为了刻画具有层次特性的网络，比如Internet网有国际连接、国家主干、区域网络、和局域网。区域网之间的点具有很高的聚类系数，彼此之间紧密相连。而区域网只通过很少的点与主干网络相连。多局域世界模型主要通过以下五个步骤进行构造

（1） 以概率p增加一个拥有m0个节点，e0条边的局域世界，代码如下：

function a=genearategraph(m0,e0);
if e0>m0*(m0-1)/2 %判断输入的参数是否有效，一个有m0个节点的网络最多有m0*(m0-1)/2条边，因此e0不可能大于这个数
    fprintf('输入的m0,e0不匹配\n');return
end
a=zeros(m0); %从这儿开始构造这个网络的邻接矩阵，用zeros函数产生m0Xm0阶的元素全为零的矩阵
ra=rand(m0); %用rand函数生成m0xmo阶的元素全为0-1之间随机数的矩阵
ra=tril(m0); %用tril函数提取ra矩阵的下三角部分
ra([1:m0+1:end])=0; %将下三角矩阵的对角线元素全部改为0，因为邻接矩阵的对角线元素必为0
[sra,indc]=sort(nonzeros(ra),'descend'); %此处nonzeros返回一个向量，这个向量是上一步矩阵所有元素按照列堆叠构成的，然后对这个向量按照降序排序
p=sra(e0) %选定前e0条边所对应的最小的概率，小于这个概率的不予保留，生成e0条边
a(ra>=p)=1;
a=a+a';
end

（2）选定一个已存在的局域世界，以概率q将一个新节点，以给定概率同局域世界中的点建立m1条边

此处先插入介绍一下轮盘赌法，这个方法在后面反复出现。
假设我们有A，B，C，D，E五个小球，各自抽中的概率为0.2，0.25，0.15，0.3，0.1

标号	1	2	3	4	5
小球	A	B	C	D	E
概率	0.2	0.25	0.1	0.15	0.3
累积概率	0.2	0.45	0.55	0.7	1

我们要实现的功能很简单，就是根据概率大小随机选抽中一个球。
我们可以这样做，用matlab的rand函数产生一个0到1之间的随机数k。用find()从累积概率向量中找到大于或者等于这个随机数k的小球的标号。比如我们产生的随机数是0.46，在累积概率中大于0.46的小球是C，D，E。其标号是3，4，5。find函数返回的就是（3，4，5）。然后我们索引到（3，4，5）中的第一个元素3。说明这次我们抽中的小球就是3号球。此处的本质是利用累积概率对0到1区间划分为5个区域。区域越大，随机数落到这个区间的概率也就越大。
下面贴上代码：

function b=addnode(a,m,alpha);%a为输入的矩阵，m为建立边的条数，alpha吸引力
b=a;n=length(a); %n为节点个数
if m>n
    return %输入数据不匹配，因为建立边的个数不可能大于整个局域世界中的节点数
end
for i=1:m %开始循环迭代生成m个点
    LP=(sum(b)+alpha)/sum(sum(b)+alpha); %计算所有点的连接的概率
    pp=cumsum(LP); %计算累积概率
    ind=find(pp>=rand); %依概率与点相连
    b(n+1,ind(1))=1;b(ind(1),n+1)=1; 
end
end

（3） 以概率r向局域世界增加m条边

function b=addedge(a,m,alpha); %a为输入的矩阵，m为加边的个数，alpha为调节的系数
 b=a;n=length(a)
 for i=1:m
     deg=sum(b); %计算当前网络各节点的度，此处返回一个向量
     LP=(deg+alpha)/sum(deg+alpha); %计算到各节点的连接概率
     pp=cumsum(LP);
     rnum=randperm(m); %产生一个全排列,即元素是1到m的整数，但是顺序是乱的,此处是为了随机设定边的一个起点
     flag=1; %初始加边的对象
     while flag<=n°(rnum(flag))==n-1 %如果当前节点已经有n-1条边，那么是加不了的
         flag=flag+1;
     end
     if flag==n+1,continue,end
     ind=find(pp>=rand);
     if rnum(flag)~=ind(1)&b(rnum(flag),ind(1))==0
         b(rnum(flag),ind(1))=1;b(ind(1),rnum(flag))=1
     end
 end
end

（4） 在一个网络中删除m条边

function b=deleteedge(a,m,alpha);
b=a;n=length(a);
for i=1:m
    deg=sum(b)
    LP=(1-(deg+alpha)/sum(deg+alpha))/(n-1); %计算各节点对应的删除概率
    pp=cumsum(LP);
    rnum=randperm(n);
    flag=1;
    while flag=rand);
    if b(rum(flag),ind(1))==1
        b(rnum(flag),ind(1))=0;b(ind(1),rnum(flag))=0; %删除原边
    end
end

(5) 以概率u在一个选定的局域世界，与其他已存在的局域世界建立m4条长程边

此处介绍一下matlab的细胞矩阵：
在matlab中，细胞数组是一种特殊的数据类型。一般组成细胞数组的元素可以是任意一种类型的常数或者常量。其数据的类型可以是字符串、双精度数、稀疏矩阵、细胞数组、结构或者其他MATLAB数据类型。
细胞数组的构建有几种方式：

%通过花括号{}创建
A={zeros(3,3,3),'jack';1.12,1:10}
%通过[]拼接细胞数组
B=[{zeros(2,2,2),{'B'};{1,23},{1:10}]
%通过cell命令
D=cell(2,3)

细胞数组的访问用{}与（）的组合

d=A{1,2}(4) 
%此处用{1，2}索引到细胞矩阵A的第一行第二列元素也就是字符元素’jack'上，然后（4）索引第四个字符k，所以此处返回k

介绍完细胞矩阵后继续贴代码

function[no,uv]=addlongedge(A,m,alpha);
    %A为所有局域世界邻接矩阵的细胞数组，A{1}为第一个邻接矩阵，m为加边的条数；no为矩阵，每个列对应两个局域世界存在连边，连边编号存放在矩阵uv的对应列中。
    n=length(A); %局域世界的个数
    no=[];
    uv=[];
    for i=1:m
        rn=randperm(n); %随机抽局域世界排列
        no=[no,rn(1:2)']; %这个排列的前个元素分别是起点局域世界和终点局域世界
        a=A{rn(1)};b=A{rn(2)} %分别挑出两个局域世界的邻接矩阵
        p1=(sum(a)+alpha)/sum(sum(a)+alpha);
        pp1=cumsum(p1);
        p2=(1-(sum(b)+alpha)/sum(sum(b)+alpha))/length(b)-1
        pp2=cumsum(p2);
        ind1=find(pp1>=rand);
        ind2=find(pp2>=rand);
        uv=[uv,[ind1(1);ind2(1)]];  
    end
    end

（6）构造局域小世界模型的主程序

clc,clear
m=5;m0=8,e0=15;p=0.3;q=0.2;r=0.25;s=0.05;u=0.2;
m1=3;m2=5;m3=4;m4=6;alpha=0.5;
p=[p,q,r,s,u];n=m
pp=cumsum(p);%依旧是用轮盘赌法来判断要执行五种方法中的哪一种方法
for 1=1:m
    A{i}=genearategraph(m0,e0);%迭代生成m个初始局域小世界
end
num(1:m)=m0;%此处的num是一个变量，前面没有出现num，但是在这里蹦出来了。这个变量量是用来存储m个局域小世界的
% 节点个数的。
for i=1:2000 % 迭代2000次
    ind=find(pp>=rand); % 轮盘赌法，此处返回一个索引向量，即大于随机数rand的两个累计概率值
    switch ind(1) % 索引到第一个大于累计概率值的对应索引，共有五种可能1，2，3，4，5。分别对应我们的五种可能
        case 1 %如果上面返回1就执行这个操作
            n=n+1; %更新局域世界个数
            A{n}=generategraph(m0,e0); % 定义细胞对象A的第n个细胞数组
            num(n)=length(A{n}); %更新num变量，将新生成的这个局域小世界的节点个数加进去
        case 2 %如果上面返回2就执行这个操作
            rn=randperm(n);%生成从1到n的整数构成的一个排列，排列是随机的，因为我们需要随机先挑一个局域世界
            k=rn(1);%索引rn向量的第一个元素相当于从从1到n中随机抽一个数。从而实现从n个小世界中随机挑一个的
            %功能。
            A{k}=addnode(A{k},m1,alpha);%使用我们前面写的函数给局域小世界加点。
            num(k)=length(A{k}); %再次更新num
        case 3 %如果上面返回3就执行这个操作
            rn=randperm(n);k=rn(1); %随机挑一个局域世界
            A{k}=addedge(A{k},m2,alpha) %执行随机加边的操作，这一步不需要更新num，因为只是加边，没有加点
        case 4 
            rn=randperm(n);k=rn(1); %随机挑选一个局域世界
            A{k}=deleteedge(A{k},m3,alpha); %随机删边
        otherwise
            [no,uv]=addlongedge(A,m4,alpha) %在局域世界中随机增加长程边，此处返回由数对组成的两个变量，
            %no是一个矩阵，有两行元素，每一列的两个元素对应每一次加边的起点局域世界编号与终点局域世界编号。
            %uv同理，每一列对应的两个元素分别对应起点局域世界内的加边的起点节点的编号与终点局域世界加边的终点
            %节点编号。
            Tno=[Tno,no];%每一次迭代后更新Tno
            Tuv=[Tuv,uv];%每一次迭代后更新Tuv
    end %switch结束
end %for循环结束
B=blkdiag(A{:}); %将细胞对象A的所有邻接矩阵按照对角线拼成一个大的邻接矩阵
num=[0,num]; %方便计算,如果不添加零的话对第一个局域世界在整个网络中的加边将会很麻烦，需要倒着索引。
cnum=cumsum(num); %计算累加
for i=1:length(Tho)%虽然大邻接矩阵拼出来了，但是局域世界之间加的边还没有在这个邻接矩阵里面加上，下面加边
    u=cnum(Tno(1,i))+Tuv(1,i); %首先利用节点累加值定位到该局域世界的起点处，然后再在起点处上根据第二项地位到
    %具体位置
    v=cnum(Tho(2,i))+Tuv(2,i); %同理上面，找到要加的边的终点在整个大网络中的位置
    B(u,v)=1;B(v,u)=1;%完成加边
end %迭代所有值，完成加边

3.12.2 多局域世界模型的度分布分析

参考《复杂网络算法与应用》上的对应内容，基本是按照其构造的规律利用平均场理论去推的，产生边的概率是推算的核心。

3.12.3 改进的多局域世界模型

第一节所介绍的多局域世界演化模型存在以下问题：

• 边的消亡机制可能会使得某一局域世界中的点成为孤立节点
• 同样，由于长程边很可能无法加到所有局域世界上去，所以一些局域世界会成为孤立的局域世界

对于这个问题书上给出了解决办法，即将度小于2的节点按照式子(3.72)和整个网络中的某个节点之间加一条边。但是这个方法只是解决了第一个问题，使得孤立节点消失，但是不能够解决第二个问题，为此我们做以下改进：

• 对于孤立节点，我们用式子（3.72）给它加边一个边。循环迭代，直到整个网络中都不存在孤立的节点。
• 对于孤立局域世界，我们逐个相连并首尾相连形成一个环状连通的网络，具体选择哪两个端点，依旧是用（3.72)

（1）孤立点加边程序

 function B=degreeaddedge(A); %输入参数A是存在孤立点的网络的邻接矩阵，输出B是加边之后的邻接矩阵
    B=A;
    while any(sum(B)<=1)  %sum(B)得到当前邻接矩阵的所有节点的度，如果有任何一个节点的度小于或者等于1
        %就执行操作
        deg=sum(B);
        p=(deg+1)/sum(deg+1); %算出当前局域世界网络所有节点的加边概率
        pp=cumsum(p); %轮盘赌法选边
        k=find(deg<=1); %找出所有度小于或者等于1的节点编号
        for i=k
            ind=find(pp>=rand);jj=ind(1); %jj为用轮盘赌法选择的节点地址
            if jj~=i %确保不会自己连到自己
                B(i,jj)=1;B(jj,i)=1;
            end
        end
    end
    end

（2）孤立的局域世界间加边的程序

此处介绍一下matlab工具箱提供的graphconncomp函数:
1.matlab图论工具箱的所有函数及其应用大家可以参考这篇博文
matlab图论工具箱介绍
可惜作者只介绍了几个常用的，咱们的这个作者偏偏没介绍，下面咱们来重点介绍一下这个graphconncomp函数
2.graphconncomp函数
对于无向图，函数返回该图的连通分支。对于有向图，返回改图的强弱连通分支。对于无向图，连通分支通俗来讲就是连通分支内的点可以互相到达，连通分支之外的点是不通的。比如下面这个图。

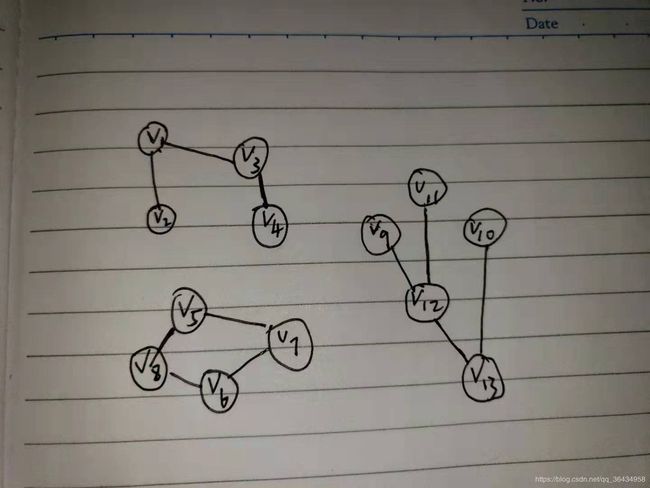
上面这个图中连通分支的个数就是三个，（1，2，3，4） （5，6，7，8） （9，10，11，12，13）
graphconncomp函数返回两个值，返回的第一个值是当前网络连通分支的个数，上面图中将会返回3，即连通分支的个数是三个。函数返回的第二个值是各个点所对应的连通分支编号，如果我们从左到右，从上至下分别将三个连通分支记为1，2，3，则此处返回向量 （1，1，1，1，2，2，2，2，3，3，3，3，3）
介绍完了，继续码代码
#-----------------------#

function B=Locworldconnect(A);
   C=tril(A);C=sparse(C);%生成稀疏矩阵
   [num,label]=graphconncomp(C,'directed',0); %这个函数是matlab工具箱里的函数，用于计算无向图连通分量.此处介绍
   %一下什么是连通分量，每一个连通分量就是点的集合，每个集合内部的点都能到达同样在集合中的点，这个函数的目的
   %就是为了把孤立的小世界挑出来，此函数返回两个参数第一个参数num表示这个图中有多少个连通分量。第二个label表
   %示每个节点的所属的分量编号。
   if num==1 %如果不存在孤立的小世界，所有的点都连接成一个大的网络，函数循环结束，直接返回B
       B==A;return
   end
   for i=1:num %对我们得到的num个连通分量开始进行迭代
       n{i}=find(label==i); %前面label得到的分量编号虽然值不同，但是所有的点都混在一起了，此处将属于第i个连通
       %分量节点的编号挑出来
   end
   B=A;deg=sum(A); %计算各节点的度
   for i=1:num
       p1=(deg(n{i})+1)/sum(deg(n{i})+1); %首先把所有属于第i个分支节点的节点的编号挑出来，利用deg()索引到这
       %这些节点的度，进而计算连接概率
       pp1=cumsum(p1); %计算累积概率，轮盘赌法选点又开始了
       ii=(i+1)*(i+1<=num)+mod(i+1,num)*(i+1>num); %此处是为了实现依次相连，第i个分支连接到第i+1个分支，之
       %所以这句写的这么麻烦是因为到最后一个分支num时，没有下一个分支和他相连，而是需要和第一个分支首尾相连形成
       %一个环，所以引入（i+1<=num)做判断是否循环到了最后一个，注意此处的运算顺序，不同于其他语言，这里
       %加法是优先于逻辑判断的，所以此处返回的是表示布尔值的0或者1.然后用mod取余数1实现定位到第一个分支。
       p2=(deg(n{ii})+1)/sum(deg(n{ii})+1); %把所有属于第i+1个节点的度给挑出来
       pp2=cumsum(p2); %计算累积概率，轮盘赌法
       ind1=find(pp1>=find); %利用概率定位连边起点
       ind2=find(pp2>=find); %利用概率定位连边终点
       B(n{i}(ind1(1)),n{ii}(ind2(1)))=1; %进行连边操作
       B(n{ii}(ind2(1)),n{i}(ind1(1)))=1;
   end   
   end

（3）改进的多局域世界网络的主程序

clc,clear
    m=5;m0=8;e0=15;p=0.3;q=0.2;r=0.25;s=0.05;u=0.2;
    m1=3;m2=5;m3=4;m4=6;alpha=1;
    p=[p,q,r,s,u];n=m;
    pp=cumsum(p); %轮盘赌法选条件
    for i=1:m
        A{i}=generategraph(m0,e0) %产生初始的m个局域世界
    end
    num(1:m)=m0; %此处先声名一个num变量，num变量的1到m个元素都是m0,此处是为了存储各个局域世界的节点个数
    Tno=[];Tuv=[]; %返回值初始化
    for i=1:2000 % 迭代2000次
    ind=find(pp>=rand); % 轮盘赌法，此处返回一个索引向量，即大于随机数rand的两个累计概率值
    switch ind(1) % 索引到第一个大于累计概率值的对应索引，共有五种可能1，2，3，4，5。分别对应我们的五种可能
        case 1 %如果上面返回1就执行这个操作
            n=n+1; %更新局域世界个数
            A{n}=generategraph(m0,e0); % 定义细胞对象A的第n个细胞数组
            num(n)=length(A{n}); %更新num变量，将新生成的这个局域小世界的节点个数加进去
        case 2 %如果上面返回2就执行这个操作
            rn=randperm(n);%生成从1到n的整数构成的一个排列，排列是随机的，因为我们需要随机先挑一个局域世界
            k=rn(1);%索引rn向量的第一个元素相当于从从1到n中随机抽一个数。从而实现从n个小世界中随机挑一个的
            %功能。
            A{k}=addnode(A{k},m1,alpha);%使用我们前面写的函数给局域小世界加点。
            num(k)=length(A{k}); %再次更新num
        case 3 %如果上面返回3就执行这个操作
            rn=randperm(n);k=rn(1); %随机挑一个局域世界
            A{k}=addedge(A{k},m2,alpha) %执行随机加边的操作，这一步不需要更新num，因为只是加边，没有加点
        case 4 
            rn=randperm(n);k=rn(1); %随机挑选一个局域世界
            A{k}=deleteedge(A{k},m3,alpha); %随机删边
        otherwise
            [no,uv]=addlongedge(A,m4,alpha) %在局域世界中随机增加长程边，此处返回由数对组成的两个变量，
            %no是一个矩阵，有两行元素，每一列的两个元素对应每一次加边的起点局域世界编号与终点局域世界编号。
            %uv同理，每一列对应的两个元素分别对应起点局域世界内的加边的起点节点的编号与终点局域世界加边的终点
            %节点编号。
            Tno=[Tno,no];%每一次迭代后更新Tno
            Tuv=[Tuv,uv];%每一次迭代后更新Tuv
    end %switch结束
    end %for循环结束
    B=blkdiag(A{:}); %将细胞对象A的所有邻接矩阵按照对角线拼成一个大的邻接矩阵
    num=[0,num]; %方便计算,如果不添加零的话对第一个局域世界在整个网络中的加边将会很麻烦，需要倒着索引。
    cnum=cumsum(num); %计算累加
    for i=1:length(Tho)%虽然大邻接矩阵拼出来了，但是局域世界之间加的边还没有在这个邻接矩阵里面加上，下面加边
        u=cnum(Tno(1,i))+Tuv(1,i); %首先利用节点累加值定位到该局域世界的起点处，然后再在起点处上根据第二项地位到
        %具体位置
        v=cnum(Tho(2,i))+Tuv(2,i); %同理上面，找到要加的边的终点在整个大网络中的位置
        B(u,v)=1;B(v,u)=1;%完成加边
    end %迭代所有值，完成加边
    B=degreeaddedge(B); %调用前面编写的函数，完成对度为0或者1的点随机加边
    B=Locworldconnect(B); %调用自己写的函数完成对孤立局域世界之间的连接。

文章结束
参考书：
《复杂网络算法与应用》孙玺菁 司守奎 国防工业出版社
《MATLAB建模与仿真实用教程》王健 赵国生 宋一兵 机械工业出版社