VGG-NET 阅读笔记

　　本论文是牛津大学 visual geometry group（VGG）Karen Simonyan 和Andrew Zisserman 于14年在Alexnet基础上撰写的论文，主要探讨了深度对于网络的重要性；并建立了一个19层的深度网络获得了很好的结果；在ILSVRC比赛上定位第一，分类第二。
　　论文于此处下载

一．概述：

---

本网络从Alex-net发展而来主要修改了两个方面：
　　1．在网络结构上，于卷积层中使用更小的filter尺寸和间隔；
　　2．在数据处理中，于整个图片上使用multi-scale训练和测试；针对multi-scale的详解见于．．．．

二．网络结构：

---

2.1　总体架构

　　　　　　　　　
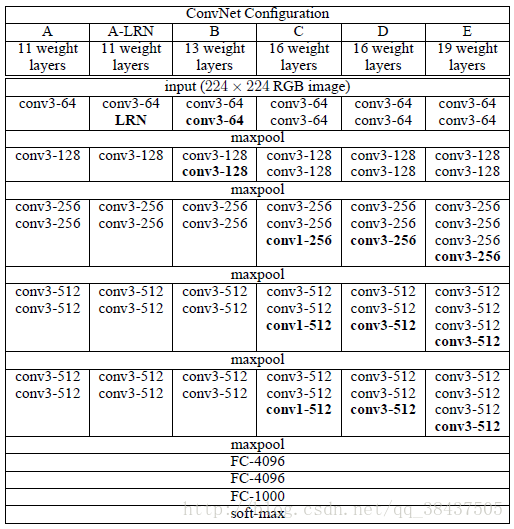
　　由作者提供的各级别网络结构图知，本结构有5个max-pooling层，是5阶卷积特征提取。每层的卷积个数从首阶段的64个开始，每个阶段增长一倍，直到达到最高的512个，然后保持。可以看到在每个阶段不再是单独的卷积，而是多个很小的卷积层（３＊３）串联在一起的（在Alex-net中基本都是１１＊１１），在每阶段末尾总是会有个１＊１的１４卷积层相连，而这些卷积层的变化正是该结构能取得更好的性能的原因．

基本结构A：

　　Input（224,224,3）→64F（3,3,3,1）→max-p(2,2)
　　→128F（3,3,64,1）→max-p(2,2)
　　→256F（3,3,128,1）→256F（3,3,256,1）→maxp(2,2)
　　→ 512F（3,3,256,1）→512F（3,3,512,1）→max-p(2,2) →512F（3,3,256,1）→512F（3,3,512,1）→max-p(2,2)
→4096fc→4096fc→1000softmax

　　8个卷积层，５个池化层，3个全连接层；作者只说明了使用3*3filter的原因，至于层数，阶段数，特征数为什么这么设计，作者并没有说明，对于这些属于结构的超参数问题很可能是在大量的实验结果的分析对比得出的。

2.2 结构特点分析

2.2.1为何采用更小的卷积核（３＊３）串联

　　１．3*3是能够捕获上下左右和中心区域信息的最小尺寸；ZFNet中说过，由于第一层中往往有大量的高频和低频信息，却没有覆盖到中间的频率信息，步长过长时，容易引起大量的混叠，因此滤波器尺寸和步长要尽量小；
　　２．多个3*3的卷积层串联不仅提升了判别函数的识别能力，而且还减少了参数；
　　　　两个卷积层的有限感受野是5*5；三个3*3的感受野是7*7，可以替代大的filter尺寸；大大减少了参数（三个3*3的卷积层参数个数3*（3*3*C*C）=27CC；一个7*7的卷积层参数为49CC；所以可以把三个3*3的filter看成是一个7*7filter的分解（中间层有非线性的分解））；　
　　　　
　　　　　　　　　　　　　
　　　　　　　　　　　　　
　　　　多个3*3的卷基层比一个大尺寸filter卷基层有更多的非线性，使得判决函数更加具有判决性 ;为什么说多了更多的非线性就有更好的识别能力呢，在当初学习激活函数的时候，我们就知道引入激活函数（激活函数都是非线性的　）就是为了在数据的映射过程中变得更加非线性，这样一模型也就越复杂，换句话说，增加了非线性后，模型能够对更为复杂的关系进行映射．　　

2.2.2每阶段末尾的１＊１卷积核有何作用

　　本篇论文中作者加入１*1的卷积核的作用是在不改变输入输出维数的情况下，对输入增加非线性，增强网络的非线性表达能力，使得其对特征的学习能力更强．
　　但是其实此时也许作者还未意识到１*１卷积核的强大，在此处作者只是运用了其　可以增强非线性的能力，没有使用其降维能力，在之后的ResNet以及ＤenseNet中，我们可以看出大量运用了１＊１的卷积核，其主要目的就是为了降维，随着网络深度　宽度的增加，模型就够很复杂，此时在宽度上就可以利用该卷积核来减少宽度．

三．网络训练：

---

• 优化方法：在训练中使用了加动量的小批基于反向传播的梯度下降法来优化多项逻辑回归目标。批数量为256，动量为0.9，权值衰减参数为5x10−4，在前两个全连接层使用dropout为0.5，学习率为0.01，且当验证集停止提升时以10的倍数衰减．
• 参数初始化过程：权重取样于高斯分布N（0，0.01），偏置项初始化为0；然后，对于较深的网络，先用A网络的参数初始化前四个卷积层和三个全连接层。但是后来发现，不用预训练的参数而直接随机初始化也可以。
• 数据集增强：（ Multi-scale训练）为了获得初始化的224x224大小的图片，通过在每张图片在每次随机梯度下降SGＤ时进行一次裁减，为了更进一步的增加训练集，对每张图片进行水平翻转以及进行随机RGB色差调整。
   　初始对原始图片进行裁剪时，原始图片的最小边不宜过小，这样的话，裁剪到224x224的时候，就相当于几乎覆盖了整个图片，这样对原始图片进行不同的随机裁剪得到的图片就基本上没差别，就失去了增加数据集的意义，但同时也不宜过大，这样的话，裁剪到的图片只含有目标的一小部分，也不是很好。
  　　针对上述裁剪的问题，提出的两种解决办法：
  　　(1) 在不同的尺度下，训练多个分类器：参数S为短边长，训练S=256和S=384两个分类器，其中S=384的分类器用S=256的进行初始化，且将步长调为10e-3；
  　　(2) 随机从[256,512]的确定范围内进行抽样来训练网络：这样原始图片尺寸不一，有利于训练，这个方法叫做尺度抖动scal jittering，有利于训练集增强， 训练时运用大量的裁剪图片有利于提升识别精确率；　　　

四．分类测试

---

　　测试阶段的方法和OverFeat测试方法相同，首先选定一个scale：Q，然后在这个图片上应用卷积网络，在最后一个卷积阶段产生unpooled　 FM，然后利用sliding window方法，每个pooling window产生一个分类输出，然后融合（取平均）各个pooling window的结果，得到最终分类。这样比10-view更加高效，只需计算一次卷积过程。（对这句话不是很明白）
　　为比较在训练和测试时对输入采取不同尺度的裁剪后，对分类性能的影响，采用不同的训练方法对模型进行训练，以便对结果进行分析．

4.1　single-scale（单尺度）:

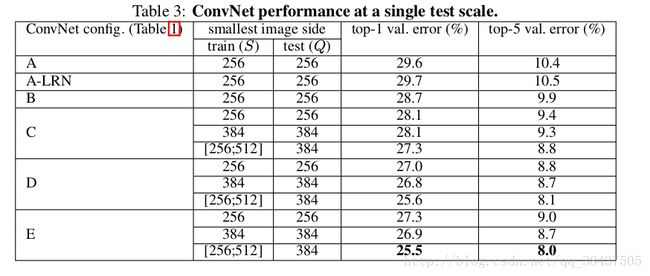
观察表格中采取的训练和测试方法：　训练数据尺寸分三种：256 384 256-512之间随机抽取，测试数据则保持单一尺度．
对比得到分析结果：
A vs A-LRN　A-LRN结果没有A好，说明LRN作用不大（LRN在后续的网络之中被弃用）；
A vs B,C,D,E：越深越好；
A vs C：增加1*1卷积核，即增加额外的非线性确实提升效果；
*C vs D：**3*3的filter比　1１　filter要好，使用较大的filter能够捕捉更大的空间特征；
训练方法：在scale区间[256;512]通过scale增益来训练网络，比在固定的两个S=256和S=384，结果明显提升。Multi-scale训练确实很有用，因为ZF论文中，卷积网络对于缩放有一定的不变性，通过multi-scale训练可以增加这种不变性的能力。

4.2　 Multi-scale　

　　观察表格训练和测试方法：　训练的数据增益和上述一样，不过在测试时，对数据进行了 Multi-scale　增益，采取不同尺寸的数据进行测试．发现在训练和测试事都采取　Multi-scale　对数据进行增益，能大大提高准确率．

4.3 模型融合　

　　在采取不同的训练方法对模型进行训练时，我们能够得到不同的结果，最终对这些结果进行融合，得到新的结果．

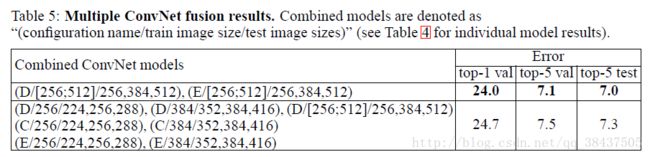
　　对这里所提到的模型融合，来求平均不是很理解，搞不懂他这个模型融合是个什么意思，到底是指最后对分类的结果直接求平均值，还是说模型模型融合，准备带着问题继续探讨，学习．

4.4和其他网络比较