Cross-modality Person re-identification with Shared-Specific Feature Transfer——论文周报
文章目录
- 1 标题
- 2 概述
- 3 创新点
- 4 算法及实验
- 4.1 模型及算法
- 双流特征提取器(Two-stream feature extractor)
- 共有-特有转移网络(Shared-Specific Transfer Network,SSTN)
- ①亲和力模型(Affinity modeling)
- ②共享和特定信息的传播
- 共有-特有互补学习(Shared and specific complementary learning)
- ①共享特征的模态自适应
- ②特定特征的投影对抗学习
- ③重建增强
- 优化
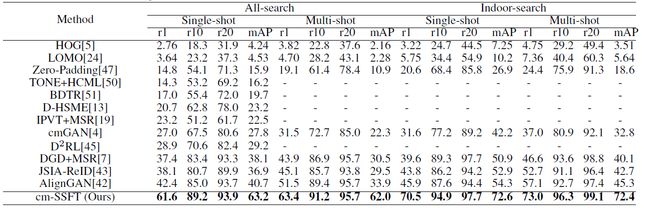
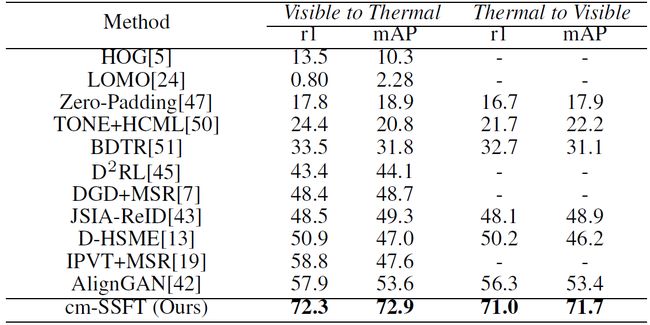
- 4.2 实验
- 5 心得
1 标题
Cross-modality Person re-identification with Shared-Specific Feature Transfer 来源:CVPR2020
2 概述
当前的跨模态行人重识别 (cm-REID)大都是把不同的模态当成同一类特征学习他们的共享特征,这种方式其实“浪费了”不同模态的特定特征(Specific Feature),每种模态的独特特征不能被提取,如红外图像独有热度特征而没有鲜明的颜色特征。(后续将混用“共享”,“共有”,混用“特定”,“特有”)
为此,作者提出了一个新颖的跨模态共有-特有特征转移(cm-SSFT)算法,以挖掘模式共享特征和特定特征在提高REID性能方面的潜力,其实模型也是一个双流网络。作者还进行了消融实验(Ablation study),比较各个结构对算法的有效性。
3 创新点
- 提出了端到端(end to end)的cm-SSFT算法,在REID问题上该算法成为了state-of -the -art;
- 提出了一种特征转移方法,在模间(inter-modality)和模内(intra-modality)根据相邻邻域进行信息传播,这可以更有效的利用每个样本的共享信息和特定信息;
- 提出了一种新颖的互补学习方法,来提取各个模态的区分性及互补性共享特征和特定特征,进一步说明了cm-SSFT算法的有效性。
4 算法及实验
4.1 模型及算法
下图为cm-SSFT模型结构,可以看出这个模型是一个双流(two-stream)网络,之前我看到的结合多种特征的网络是双分支(two branch)网络,我目前还不清楚两种定义指的是不是一类网络,需要进一步调研。
模型中,R代表RGB,I代表红外,H代表共享特征,P代表特定特征,整个模型的训练是端到端的方式,模型的工作流程如下:①先将输入图片(包括RGB与红外)送到双流特征提取器中,提取它们的特有特征与共享特征;②然后在不同的模态之间传播共享特征与特定特征,以补偿缺少的特定信息,加强共享信息;③在特征提取器上加入了2个投影对抗与重构(project adversarial and reconstruction)块和1个模态自适应模块(modality adaptation),以获得更具区分性和互补性的共享特征及特定特征。
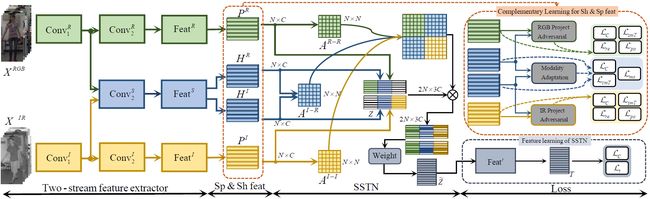
双流特征提取器(Two-stream feature extractor)
包含一个模态共享特征流(蓝色块),以及模态特有特征流(绿色的RGB,黄色的红外),为了更好的性能表现,在浅层卷积层就将shared流和specific流分开,而不是后面的FC层,输入图片 X m m ∈ { R , I } X^m\,\,m\in{\{R,I\}} Xmm∈{R,I},有: H m = F e a t S ( C o n v 2 S ( C o n v 1 m ( X m ) ) ) H^m=Feat^S(Conv_2^S(Conv_1^m(X^m))) Hm=FeatS(Conv2S(Conv1m(Xm))) P m = F e a t m ( C o n v 2 m ( C o n v 1 m ( X m ) ) ) P^m=Feat^m(Conv_2^m(Conv_1^m(X^m))) Pm=Featm(Conv2m(Conv1m(Xm)))
为了保证两种特征更有区分性,作者还为两个特征分别增加了分类损失 L c L_c Lc, p ( y i m | ∗ ) p\left(y_i^m\middle|\ast\right) p(yim∣∗)是图片 X m X^m Xm属于真正类别 y i m y_i^m yim的可能性: L c ( H m ) = E i , m [ − log ( p ( y i m ∣ H i m ) ) ] L_c(H^m)=\mathbb{E}_{i,m}[-\log{(p(y^m_i|H_i^m))}] Lc(Hm)=Ei,m[−log(p(yim∣Him))] L c ( P m ) = E i , m [ − log ( p ( y i m ∣ P i m ) ) ] L_c(P^m)=\mathbb{E}_{i,m}[-\log{(p(y^m_i|P_i^m))}] Lc(Pm)=Ei,m[−log(p(yim∣Pim))]
此外,也是为了保证更好的区分性,作者为特定特征添加了一个单模态三元组损失 L s m T L_{smT} LsmT,为共享特征添加了一个跨模态三元组损失 L c m T L_{cmT} LcmT,其中 ρ 1 \rho_1 ρ1, ρ 2 \rho_2 ρ2是损失函数的margin,而 i , j , k i,j,k i,j,k则分别代表triplet loss中的anchor,positive和negative:
L s m T = ∑ i , j , k m a x [ ρ 2 + ∣ ∣ P i R − P j R ∣ ∣ − ∣ ∣ P i R − P k R ∣ ∣ , 0 ] + ∑ i , j , k m a x [ ρ 2 + ∣ ∣ P i I − P j I ∣ ∣ − ∣ ∣ P i I − P k I ∣ ∣ , 0 ] L c m T = ∑ i , j , k m a x [ ρ 1 + ∣ ∣ H i R − H j I ∣ ∣ − ∣ ∣ H i R − H k I ∣ ∣ , 0 ] + ∑ i , j , k m a x [ ρ 1 + ∣ ∣ H i I − H j R ∣ ∣ − ∣ ∣ H i I − H k R ∣ ∣ , 0 ] \begin{aligned} L_{smT}=&\sum_{i,j,k}max[\rho_2+||P_i^R-P_j^R||-||P_i^R-P_k^R||,0]\\+&\sum_{i,j,k}max[\rho_2+||P_i^I-P_j^I||-||P_i^I-P_k^I||,0]\\L_{cmT}=&\sum_{i,j,k}max[\rho_1+||H_i^R-H_j^I||-||H_i^R-H_k^I||,0]\\+&\sum_{i,j,k}max[\rho_1+||H_i^I-H_j^R||-||H_i^I-H_k^R||,0] \end{aligned} LsmT=+LcmT=+i,j,k∑max[ρ2+∣∣PiR−PjR∣∣−∣∣PiR−PkR∣∣,0]i,j,k∑max[ρ2+∣∣PiI−PjI∣∣−∣∣PiI−PkI∣∣,0]i,j,k∑max[ρ1+∣∣HiR−HjI∣∣−∣∣HiR−HkI∣∣,0]i,j,k∑max[ρ1+∣∣HiI−HjR∣∣−∣∣HiI−HkR∣∣,0]
共有-特有转移网络(Shared-Specific Transfer Network,SSTN)
为了统一特征表示,将每个模态的特征以三段式(RGB,共享,红外)表示:
Z i R = [ P i R ; H i R ; 0 ] , Z i I = [ 0 ; H j I , P j I ] Z_i^R=[P_i^R;H_i^R;0],\,\,\,Z_i^I=[0;H_j^I,P_j^I] ZiR=[PiR;HiR;0],ZiI=[0;HjI,PjI]
0代表填充的零向量,很显然,RGB模态没有红外特征,红外模态没有RGB特征,所以对应位置为0,而[;]表示在列维度上级联(拼接),收到GCN(graph convolutional network)的启发,作者利用近邻来传播信息。SSTN弥补了特定特征的不足,同时提高了整体表示的鲁棒性。
①亲和力模型(Affinity modeling)
用共享特征和特定特征组建亲和力对(pair-wise affinit)模型,利用特定特征计算模内亲和力,用共享特征计算模间亲和力:
A i , j m , m = d ( P i m , P j m ) , A i , j m , m ′ = d ( H i m , H j m ′ ) A_{i,j}^{m,m}=d(P_i^m,P_j^m),\,\,\,A_{i,j}^{m,m'}=d(H_i^m,H_j^{m'}) Ai,jm,m=d(Pim,Pjm),Ai,jm,m′=d(Him,Hjm′) A i , j m , m A_{i,j}^{m,m} Ai,jm,m是模态m中第i个样本和第j个样本的模内亲和力, A i , j m , m ′ A_{i,j}^{m,m^\prime} Ai,jm,m′是模间亲和力, d ( a , b ) d\left(a,b\right) d(a,b)表示归一化的欧氏距离:
d ( a , b ) = 1 − 0.5 ⋅ ∣ ∣ a ∣ ∣ a ∣ ∣ − b ∣ ∣ b ∣ ∣ ∣ ∣ d(a,b)=1-0.5·\left|\left|\frac{a}{||a||}-\frac{b}{||b||}\right|\right| d(a,b)=1−0.5⋅∣∣∣∣∣∣∣∣∣∣a∣∣a−∣∣b∣∣b∣∣∣∣∣∣∣∣
模内和模间相似度表示了每个样本与其他相同或不同模态之间的关系,最终的亲和力矩阵定义为: A = [ τ ( A R , R , k ) τ ( A R , I , k ) τ ( A I , R , k ) τ ( A I , I , k ) ] A=\left[\begin{matrix}\tau{(A}^{R,R},k)&\tau{(A}^{R,I},k)\\\tau{(A}^{I,R},k)&\tau{(A}^{I,I},k)\\\end{matrix}\right] A=[τ(AR,R,k)τ(AI,R,k)τ(AR,I,k)τ(AI,I,k)]
其中 τ ⋅ , k \tau·,k τ⋅,k是近邻选择函数,它保留矩阵每一行的前 k k k个值,其他的置为0。
②共享和特定信息的传播
亲和力矩阵代表样本之间的相似性,而SSTN利用这个矩阵传播特征,此前,RGB特征和红外模态已经在行维度上拼接,每一个存储一个样本特征:
Z ~ = [ Z ~ R Z ~ I ] \widetilde{Z}=\left[\begin{matrix}\widetilde{Z}^R\\\widetilde{Z}^I\\\end{matrix}\right] Z =[Z RZ I]
在进行特征融合之后,传播的特征将包括两种模态的共享特征和特定特征: Z ~ = [ Z ~ R Z ~ I ] = σ ( D − 1 2 A D − 1 2 Z W ) \widetilde{Z}=\left[\begin{matrix}\widetilde{Z}^R\\\widetilde{Z}^I\\\end{matrix}\right]=\sigma\left(D^{-\frac{1}{2}}AD^{-\frac{1}{2}}ZW\right) Z =[Z RZ I]=σ(D−21AD−21ZW)
亲和力矩阵 A A A的对角阵 D D D是通过GCN方法得到的,其中 d i i = ∑ j A i j d_{ii}=\sum_{j}^{\ }A_{ij} dii=∑j Aij, σ \sigma σ是激活函数,作者用的是ReLU, W W W是SSTN的可学习参数,这些传播的特征最后被送入特征学习阶段来优化整个学习过程,转移特征T记为: T = [ T R T I ] = F e a t t Z T=\left[\begin{matrix}T^R\\T^I\\\end{matrix}\right]=Feat^tZ T=[TRTI]=FeattZ
遵循通用特征学习原理,使用分类损失来进行特征学习:
L c ( T m ) = E i , m [ − log ( p ( y i m | T i m ) ) ] L_c\left(T^m\right)=E_{i,m}\left[-\log{\left(p\left(y_i^m\middle|\ T_i^m\right)\right)}\right] Lc(Tm)=Ei,m[−log(p(yim∣ Tim))]
此外,在转移特征上,和前面一样利用三元组损失来增强辨别性,因为转移特征包含了两种模态的共享特征和特定特征:
L t ( T ) = L c m T ( T ) + L s m T ( T ) = ∑ i , j , k m a x [ ρ 1 + ∣ ∣ T i R − T j I ∣ ∣ − ∣ ∣ T i R − T k I ∣ ∣ , 0 ] + ∑ i , j , k m a x [ ρ 1 + ∣ ∣ T i I − T j R ∣ ∣ − ∣ ∣ T i I − T k R ∣ ∣ , 0 ] + ∑ i , j , k m a x [ ρ 2 + ∣ ∣ T i R − T j R ∣ ∣ − ∣ ∣ T i R − T k R ∣ ∣ , 0 ] + ∑ i , j , k m a x [ ρ 2 + ∣ ∣ T i I − T j I ∣ ∣ − ∣ ∣ T i I − T k I ∣ ∣ , 0 ] \begin{aligned} L_{t}(T)=L_{cmT}(T)+L_{smT}(T)=&\sum_{i,j,k} m a x\left[\rho_1+\left|\left|T_i^R-T_j^I\right|\right|-\left|\left|T_i^R-T_k^I\right|\right|,0\right]\\+&\sum_{i,j,k} m a x\left[\rho_1+\left|\left|T_i^I-T_j^R\right|\right|-\left|\left|T_i^I-T_k^R\right|\right|,0\right]\\+&\sum_{i,j,k} m a x\left[\rho_2+\left|\left|T_i^R-T_j^R\right|\right|-\left|\left|T_i^R-T_k^R\right|\right|,0\right]\\+&\sum_{i,j,k} m a x\left[\rho_2+\left|\left|T_i^I-T_j^I\right|\right|-\left|\left|T_i^I-T_k^I\right|\right|,0\right] \end{aligned} Lt(T)=LcmT(T)+LsmT(T)=+++i,j,k∑max[ρ1+∣∣∣∣TiR−TjI∣∣∣∣−∣∣∣∣TiR−TkI∣∣∣∣,0]i,j,k∑max[ρ1+∣∣∣∣TiI−TjR∣∣∣∣−∣∣∣∣TiI−TkR∣∣∣∣,0]i,j,k∑max[ρ2+∣∣∣∣TiR−TjR∣∣∣∣−∣∣∣∣TiR−TkR∣∣∣∣,0]i,j,k∑max[ρ2+∣∣∣∣TiI−TjI∣∣∣∣−∣∣∣∣TiI−TkI∣∣∣∣,0]
共有-特有互补学习(Shared and specific complementary learning)
共享特征和特定特征之间的信息重叠也会影响整体模型性能,为此,作者利用模态自适应从共享特征中过滤掉模态特定信息,作者也为互补性特定特征学习提出了投影对抗策略和重建增强方法。
①共享特征的模态自适应
为了提纯模态无关的共享特征,作者用带3个FC层的模态辨别器(discriminator)对每个共享特征的模态进行分类, Θ D \Theta_D ΘD代表模态辨别器的参数, p ( m | H i m ) p\left(m\middle| H_i^m\right) p(m∣Him)是特征 H i m H_i^m Him属于模态 m m m的概率,在鉴别阶段,模态鉴别器试着对每个共享特征的模态进行分类,在生成阶段,backbone网络会生成特征来骗过鉴别器,这个min-max游戏会使得共享特征不包含任何模态相关的信息: L m a = E i , m [ − log ( p ( m ∣ H i m , Θ D ) ) ] L_{ma}=\mathbb{E}_{i,m}[-\log(p(m|H_i^m,\Theta_D))] Lma=Ei,m[−log(p(m∣Him,ΘD))]
②特定特征的投影对抗学习
为了使特定特征与共享特征不相关,作者提出了投影对抗策略,在训练阶段,将特定特征投影到同一个样本的共享特征上,投影误差作为损失函数, Θ m \Theta^m Θm是模态 m m m的投影矩阵,“·”表示矩阵相乘。在鉴别阶段,对 Θ p m \Theta_p^m Θpm的优化会试着将特定特征投影到对应的共享特征上,在生成阶段,backbone网会生成与共享特征不相关的特定特征来骗过投影: L p a = E i , m [ ∣ ∣ Θ m ⋅ P i m − H i m ∣ ∣ ] L_{pa}=\mathbb{E}_{i,m}[||\Theta^m·P_i^m-H_i^m||] Lpa=Ei,m[∣∣Θm⋅Pim−Him∣∣]
③重建增强
前面的工作使两种特征不会包含彼此相关的信息,为了使两种特征互补,在每个模态特征后使用解码器网络来重构输入,将两种特征级联送给解码器 D e De De: x ^ m = D e m ( [ P m ; H m ] ) \hat{x}^m=De^m([P^m;H^m]) x^m=Dem([Pm;Hm])
其中[;]代表特征级联,用L_2损失评估重建图像的质量: L r e = E i , m [ L 2 ( X i m , X ^ i m ) ] L_{re}=\mathbb{E}_{i,m}[L_2(X_i^m,\hat{X}_i^m)] Lre=Ei,m[L2(Xim,X^im)]
优化
利用分类与三元组混合损失: L ( H ) = L c ( H m ) + 0.5 ⋅ L c m T L ( P ) = 0.5 ⋅ ( L c ( P R ) + L c ( P I ) ) + 0.5 ⋅ L s m T L ( T ) = L c ( T ) + 0.25 ⋅ L t ( T ) \begin{aligned}L(H)&=L_c(H^m)+0.5·L_{cmT}\\L(P)&=0.5·(L_c(P^R)+L_c(P^I))+0.5·L_{smT}\\L(T)&=L_c(T)+0.25·L_t(T)\end{aligned} L(H)L(P)L(T)=Lc(Hm)+0.5⋅LcmT=0.5⋅(Lc(PR)+Lc(PI))+0.5⋅LsmT=Lc(T)+0.25⋅Lt(T)
认为backbone和SSTN同等重要:
L f e a t = L ( H ) + L ( P ) + L ( T ) L_{feat}=L(H)+L(P)+L(T) Lfeat=L(H)+L(P)+L(T)
每个部分min-max步骤的损失函数: L m i n = L f e a t + λ 1 L r e − λ 2 L m a − λ 3 L p a L m a x = − λ 2 L m a − λ 3 L p a \begin{aligned}L_{min}&=L_{feat}+\lambda_1L_{re}-\lambda_2L_{ma}-\lambda_3L_{pa}\\L_{max}&=-\lambda_2L_{ma}-\lambda_3L_{pa}\end{aligned} LminLmax=Lfeat+λ1Lre−λ2Lma−λ3Lpa=−λ2Lma−λ3Lpa
优化过程包含两个子过程,1)固定每个鉴别器,最小化 L m i n L_{min} Lmin;2)固定除三个鉴别器外的所有模块,最大化 L m a x L_{max} Lmax。 Θ N \Theta_N ΘN是除鉴别器外的整个网络的参数: Θ ^ N = a r g Θ N m i n L m i n ( Θ N , Θ ^ D , Θ ^ m ) Θ ^ D , Θ ^ m = a r g Θ D Θ m m a x L m a x ( Θ ^ N , Θ D , Θ m ) \begin{aligned}\hat\Theta_N&=arg_{\Theta_N}minL_{min}(\Theta_N,\hat\Theta_D,\hat\Theta^m)\\\hat\Theta_D,\hat\Theta^m&=arg_{\Theta_D\,\Theta^m}maxL_{max}(\hat\Theta_N,\Theta_D,\Theta^m)\end{aligned} Θ^NΘ^D,Θ^m=argΘNminLmin(ΘN,Θ^D,Θ^m)=argΘDΘmmaxLmax(Θ^N,ΘD,Θm)
4.2 实验
5 心得
inter:不同事物之间,intra:同一事物内部各部分之间,刚开始把这两个概念搞混了,intra-modality是模内特征,inter-modality是模间特征。
这篇文章是讲的跨模态REID,当前的几个经典REID数据集上准确率已经被刷得很高了,而且有监督方法几乎很难突破,无监督方法和半监督方法REID的模型性能也提高的很快,所以从这方面下手也有些困难,不过目前自监督好像还没人做,也不知道可行不可行。跨模态还是值得作为一个方向的,下一步考虑多看些跨模态REID,并运行一些跨模态的开源项目。
此外,双流网络和双分支网络到底是不是一类网络,还是两个不同的概念?需要进一步调研。