机器学习+python --多元线性回归模型
具体公式暂未深入理解,只有一些代码的调用。
学习时一些参考的文档
scikit-learn库中有自带的数据集,比如糖尿病病人数据集
1.样本数量442
2.每个样本10个特征
3.特征为浮点数,数据在-0.2~0.2之间
4.样本的目标在整数25~346之间
1.针对全部特征进行回归:
# -*- coding: utf-8 -*-
"""
广义线性模型
~~~~~~~~~~~~~~~~~~~~~~~~~~
LinearRegression
:copyright: (c) 2016 by the huaxz1986.
:license: lgpl-3.0, see LICENSE for more details.
"""
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model,cross_validation
from sklearn.cross_validation import train_test_split
def load_data():
'''
加载用于回归问题的数据集
:return: 一个元组,用于回归问题。元组元素依次为:训练样本集、测试样本集、训练样本集对应的值、测试样本集对应的值
'''
diabetes = datasets.load_diabetes()#使用 scikit-learn 自带的一个糖尿病病人的数据集
return train_test_split(diabetes.data,diabetes.target,
test_size=0.25,random_state=0) # 拆分成训练集和测试集,测试集大小为原始数据集大小的 1/4
def test_LinearRegression(*data):
'''
测试 LinearRegression 的用法
:param data: 可变参数。它是一个元组,这里要求其元素依次为:训练样本集、测试样本集、训练样本的值、测试样本的值
:return: None
'''
X_train,X_test,y_train,y_test=data
regr = linear_model.LinearRegression()
regr.fit(X_train, y_train)
print X_train[:,np.newaxis,0].shape
print('Coefficients:%s, intercept %.2f'%(regr.coef_,regr.intercept_))
print("Residual sum of squares: %.2f"% np.mean((regr.predict(X_test) - y_test) ** 2))
print('Score: %.2f' % regr.score(X_test, y_test))
if __name__=='__main__':
X_train,X_test,y_train,y_test=load_data() # 产生用于回归问题的数据集
test_LinearRegression(X_train,X_test,y_train,y_test) # 调用 test_LinearRegression运算结果:
Coefficients:[ -43.26774487 -208.67053951 593.39797213 302.89814903 -560.27689824
261.47657106 -8.83343952 135.93715156 703.22658427 28.34844354], intercept 153.07
Residual sum of squares: 3180.20
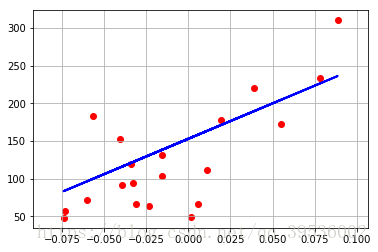
Score: 0.362.只针对一个特征进行回归:
from sklearn import datasets,linear_model,discriminant_analysis
import numpy as np
import matplotlib.pyplot as plt
def load_data():
diabetes=datasets.load_diabetes()#导入数据
print (diabetes.data.shape)#数据的大小 返回(442,10)有是个特征
print (diabetes.target.shape)
diabetes_X = diabetes.data[:, np.newaxis, 2]#利用numpy-newaxis将数据行和列颠倒一下,取第三行即为第三个特征数据
print(diabetes_X.shape)#返回(442,1)
diabetes_X_train=diabetes_X[:-20]#取422个样本作为训练样本
diabetes_X_test=diabetes_X[-20:]#后20个作为测试样本
diabetes_y_train=diabetes.target[:-20]#同理
diabetes_y_test=diabetes.target[-20:]
return diabetes_X_train,diabetes_y_train,diabetes_X_test,diabetes_y_test
#返回值为:训练样本特征x,和训练样本目标y,测试样本特征x,测试样本目标
def test_LinearRegrssion(*data):
data = load_data()
regr = linear_model.LinearRegression()
regr.fit(data[0],data[1])#利用训练样本进行魔性训练
plt.scatter(data[2], data[3], c='red')#将测试样本及画出来
plt.plot(data[2], regr.predict(data[2]), color='blue', linewidth=2)
print data[2].shape
print data[3].shape
print('Coefficients:%s,intercept %.2f' % (regr.coef_, regr.intercept_))
print("Residual sum of square:%.2f" % np.mean((regr.predict(data[2]) - data[3]) ** 2))#均方误差
print('Score:%.2f' % regr.score(data[2], data[3]))#得分,值越接近1,效果越好,也可为负数,训练效果很差的情况下
plt.grid()
plt.show()
test_LinearRegrssion()运算结果:
(442L, 10L)
(442L,)
(442L, 1L)
(20L, 1L)
(20L,)
Coefficients:[938.23786125],intercept 152.92
Residual sum of square:2548.07
Score:0.47
3.分别对各个特征进行回归:
# -*- coding: utf-8 -*-
"""
广义线性模型
~~~~~~~~~~~~~~~~~~~~~~~~~~
LinearRegression
:copyright: (c) 2016 by the huaxz1986.
:license: lgpl-3.0, see LICENSE for more details.
"""
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model,cross_validation
from sklearn.cross_validation import train_test_split
def load_data():
'''
加载用于回归问题的数据集
:return: 一个元组,用于回归问题。元组元素依次为:训练样本集、测试样本集、训练样本集对应的值、测试样本集对应的值
'''
diabetes = datasets.load_diabetes()#使用 scikit-learn 自带的一个糖尿病病人的数据集
return train_test_split(diabetes.data,diabetes.target,
test_size=0.25,random_state=0) # 拆分成训练集和测试集,测试集大小为原始数据集大小的 1/4
def test_LinearRegression(*data):
'''
测试 LinearRegression 的用法
:param data: 可变参数。它是一个元组,这里要求其元素依次为:训练样本集、测试样本集、训练样本的值、测试样本的值
:return: None
'''
X_train,X_test,y_train,y_test=data
regr = linear_model.LinearRegression()
plt.subplot(5,2,1)
plt.scatter(X_test[:, np.newaxis,0], y_test, c='red')
regr.fit(X_train[:, np.newaxis,0], y_train)
plt.plot(X_test[:, np.newaxis,0],regr.predict(X_test[:, np.newaxis,0]),color='blue')
plt.subplot(5,2,2)
plt.scatter(X_test[:, np.newaxis,1], y_test, c='red')
regr.fit(X_train[:, np.newaxis,1], y_train)
plt.plot(X_test[:, np.newaxis,1],regr.predict(X_test[:, np.newaxis,1]),color='blue')
plt.subplot(5,2,3)
plt.scatter(X_test[:, np.newaxis,2], y_test, c='red')
regr.fit(X_train[:, np.newaxis,2], y_train)
plt.plot(X_test[:, np.newaxis,2],regr.predict(X_test[:, np.newaxis,2]),color='blue')
plt.subplot(5,2,4)
plt.scatter(X_test[:, np.newaxis,3], y_test, c='red')
regr.fit(X_train[:, np.newaxis,3], y_train)
plt.plot(X_test[:, np.newaxis,3],regr.predict(X_test[:, np.newaxis,3]),color='blue')
plt.subplot(5,2,5)
plt.scatter(X_test[:, np.newaxis,4], y_test, c='red')
regr.fit(X_train[:, np.newaxis,4], y_train)
plt.plot(X_test[:, np.newaxis,4],regr.predict(X_test[:, np.newaxis,4]),color='blue')
plt.subplot(5,2,6)
plt.scatter(X_test[:, np.newaxis,5], y_test, c='red')
regr.fit(X_train[:, np.newaxis,5], y_train)
plt.plot(X_test[:, np.newaxis,5],regr.predict(X_test[:, np.newaxis,5]),color='blue')
plt.subplot(5,2,7)
plt.scatter(X_test[:, np.newaxis,6], y_test, c='red')
regr.fit(X_train[:, np.newaxis,6], y_train)
plt.plot(X_test[:, np.newaxis,6],regr.predict(X_test[:, np.newaxis,6]),color='blue')
plt.subplot(5,2,8)
plt.scatter(X_test[:, np.newaxis,7], y_test, c='red')
regr.fit(X_train[:, np.newaxis,7], y_train)
plt.plot(X_test[:, np.newaxis,7],regr.predict(X_test[:, np.newaxis,7]),color='blue')
plt.subplot(5,2,9)
plt.scatter(X_test[:, np.newaxis,8], y_test, c='red')
regr.fit(X_train[:, np.newaxis,8], y_train)
plt.plot(X_test[:, np.newaxis,8],regr.predict(X_test[:, np.newaxis,8]),color='blue')
plt.subplot(5,2,10)
plt.scatter(X_test[:, np.newaxis,9], y_test, c='red')
regr.fit(X_train[:, np.newaxis,9], y_train)
plt.plot(X_test[:, np.newaxis,9],regr.predict(X_test[:, np.newaxis,9]),color='blue')
plt.show
regr.fit(X_train, y_train)
print('Coefficients:%s, intercept %.2f'%(regr.coef_,regr.intercept_))
print("Residual sum of squares: %.2f"% np.mean((regr.predict(X_test) - y_test) ** 2))
print('Score: %.2f' % regr.score(X_test, y_test))
if __name__=='__main__':
X_train,X_test,y_train,y_test=load_data() # 产生用于回归问题的数据集
test_LinearRegression(X_train,X_test,y_train,y_test) # 调用 test_LinearRegression运行结果: