《进化算法的平均收敛速率》论文复现
摘要:此次博客主要是Jun He和Guangming Lin《进化算法的平均收敛速率》学习心得[1],推导了在离散优化中平均收敛速率的下界,并且使用python3.6复现了论文中提到的the multigrid EA (MEA)[2],the fast evolutionary programming (FEP)[3]以及the (1+1) EA[4]。除此之外,使用这三个算法在Ackley’s function和OneMax function问题上进行了平均收敛速率的计算,仿真结果也反应了理论推导的正确性。
关键字:平均收敛率,MEA,FEP,(1+1)EA,马尔科夫链
I.收敛速率简介
由于进化算法(EA)是迭代式方法,因此EA收敛到最优值的速度有多快一直是一个热点问题。遗传算法收敛速度现在可分为两种,第一种和EA转换矩阵的特征值有关,第二种是基于Doeblin条件(整个目标空间 X N X^N XN的minorization条件:如果在 X N X^N XN存在一个概率测量 ψ \psi ψ,对于正整数 t 0 t_0 t0、正数 δ > 0 \delta >0 δ>0以及所有可测量的子集 A ⊆ X N A\subseteq X^N A⊆XN,有转移函数 $ P(1,t_0;x,A) \geqslant \delta \psi(A) , x \in X^N$))。
将EA建模成一个有限的马尔科夫链,其转换矩阵为P,其每一个状态为一个种群。令 p t p_t pt是在种群空间中第t代种群的概率分布, π \pi π是P的一个平稳分布( π P = π \pi P=\pi πP=π)。如果 l i m t → ∞ ∣ ∣ p t − π ∣ ∣ = 0 lim_{t\rightarrow \infty}||p_t-\pi||=0 limt→∞∣∣pt−π∣∣=0,称 p t p_t pt收敛于$ \pi 。 这 里 。这里 。这里||*|| 是 一 个 范 数 。 收 敛 速 度 是 指 是一个范数。收敛速度是指 是一个范数。收敛速度是指p_t 以 多 快 的 速 度 收 敛 于 以多快的速度收敛于 以多快的速度收敛于\pi 。 目 的 是 获 得 一 个 界 。目的是获得一个界 。目的是获得一个界\beta(t)$使得
∣ ∣ p t − π ∣ ∣ ⩽ β ( t ) ||p_t-\pi||\leqslant \beta(t) ∣∣pt−π∣∣⩽β(t)。
II.平均收敛速率定义
考虑最小化或者最大化函数 f ( x ) f(x) f(x),EA的迭代步骤如下:初始化构造一个种群的解集 ϕ 0 \phi_0 ϕ0,然后产生一个种群序列 ϕ 0 , ϕ 1 , ϕ 2 , . . . \phi_0,\phi_1,\phi_2,... ϕ0,ϕ1,ϕ2,...。重复这个过程直到满足停止条件。在此过程中记录每代找到的最优解。
定义种群 ϕ t \phi_t ϕt的适应度为其所有个体的最优适应度值,记做 f ( ϕ t ) f(\phi_t) f(ϕt)。因为 f ( ϕ t ) f(\phi_t) f(ϕt)是一个随机向量,我们定义其期望值为 f t : = E [ f ( ϕ t ) ] f_t:=E[f(\phi_t)] ft:=E[f(ϕt)],定义 f o p t f_{opt} fopt为最优适应度。综上定义一代的收敛速率为
∣ f o p t − f t f o p t − f t − 1 ∣ |\frac{f_{opt}-f_t}{f_{opt}-f_{t-1}}| ∣fopt−ft−1fopt−ft∣
因为 f o p t − f t ≈ f o p t − f t − 1 f_{opt}-f_t\approx f_{opt}-f_{t-1} fopt−ft≈fopt−ft−1,以上的收敛速率是不稳定的。因此提出以下平均收敛速率
R ( t ∣ ϕ 0 ) : = 1 − ( ∣ f o p t − f 1 f o p t − f 0 ∣ . . . ∣ f o p t − f t f o p t − f t − 1 ∣ ) 1 / t = 1 − ( ∣ f o p t − f t f o p t − f 0 ∣ ) 1 / t R(t|\phi_0):=1-(|\frac{f_{opt}-f_1}{f_{opt}-f_{0}}|...|\frac{f_{opt}-f_t}{f_{opt}-f_{t-1}}|)^{1/t}=1-(|\frac{f_{opt}-f_t}{f_{opt}-f_{0}}|)^{1/t} R(t∣ϕ0):=1−(∣fopt−f0fopt−f1∣...∣fopt−ft−1fopt−ft∣)1/t=1−(∣fopt−f0fopt−ft∣)1/t
如果 f o p t = f 0 f_{opt}=f_0 fopt=f0,令 R ( t ∣ ϕ 0 ) = 1 R(t|\phi_0)=1 R(t∣ϕ0)=1。以下简写 R ( t ∣ ϕ 0 ) R(t|\phi_0) R(t∣ϕ0)为 R ( t ) R(t) R(t)。
公式(2)其实代表每代适应度差的归一化几何平均值。收敛速率越大,收敛的越快。最大收敛率为1.
根据平均收敛速率的定义,设计其计算步骤如下:
1)运行T次EA(T>>1);
2)计算 f t f_t ft的均值:
f t = 1 T ( f ( ϕ t [ 1 ] ) + . . . + f ( ϕ t [ T ] ) ) f_t=\frac{1}{T}(f(\phi_{t}^{[1]})+...+f(\phi_{t}^{[T]})) ft=T1(f(ϕt[1])+...+f(ϕt[T]))
这里定义 f ( ϕ t [ k ] ) f(\phi_{t}^{[k]}) f(ϕt[k])为第k次运行地适应度值 f ( ϕ t ) f(\phi_{t}) f(ϕt)。当T趋近于无穷时,(3)式即为适应度值的期望。
3)最后根据公式(2)计算R(t)。
III.使用FEP和MEA处理Ackley’s function问题的平均收敛速率
1.Ackley’s function
此处以Ackley’s function为优化目标,是一个复杂的多模态函数,其定义式如下:
f ( x ) = − 20 e − 0.2 [ ∑ i = 1 n ( x i + e ) 2 / n ] 1 / 2 − e ∑ i = 1 n c o s ( 2 π x i + 2 π e ) / n + 20 + e f(x)=-20e^{-0.2[\sum_{i=1}^{n}(x_i+e)^2/n]^{1/2}}-e^{\sum_{i=1}^{n}cos(2\pi x_i+2\pi e)/n}+20+e f(x)=−20e−0.2[∑i=1n(xi+e)2/n]1/2−e∑i=1ncos(2πxi+2πe)/n+20+e
这里 x i ∈ [ − 32 − e , 32 − e ] , i = 1 , . . . , n x_i \in [-32-e,32-e],i=1,...,n xi∈[−32−e,32−e],i=1,...,n,其最优解为0。
2.the multigrid EA
2.1简介
多重网格法是一种加速数值算法收敛速度的有效方法。MEA将多重网格法和进化算法相结合从而加快算法的收敛速度。考虑最优化问题:
a r g m i n f ( x ) , x ∈ S argminf(x),x\in S argminf(x),x∈S
这里 S ∈ R n S\in R^n S∈Rn(n是维度)。假设 f ( x ) f(x) f(x)在S上连续,那么S上其至少有一个最小值点。假设S是一个超立方体,如 S = [ a 1 , b 1 ] × , . . . , × [ a n , b n ] S=[a_1,b_1]\times,...,\times[a_n,b_n] S=[a1,b1]×,...,×[an,bn]。那么一个网格 S h S_h Sh是定义域S上的一组点,定义为 S h = ( a 1 + i 1 h , . . . , a n + i n h ) ∈ S , i 1 , . . . , i n ∈ Z S_h={(a_1+i_1h,...,a_n+i_nh)\in S,i_1,...,i_n\in Z} Sh=(a1+i1h,...,an+inh)∈S,i1,...,in∈Z。这里h是一个网格大小,Z是整数的集合。
网格法就是将定义域划分为不同的网格层。给定一个网格大小序列 h 1 , h 2 , . . . , h L h_1,h_2,...,h_L h1,h2,...,hL满足 h 1 > h 2 > . . . > h L > 0 h_1>h_2>...>h_L>0 h1>h2>...>hL>0,然后将定义域S划分为不同层的网格 S h 1 , S h 2 , . . . S , h L S_{h_1},S_{h_2},...S_{,h_L} Sh1,Sh2,...S,hL,这里 S h l S_{h_l} Shl的网格大小为 h l h_l hl。为了简单起见,我们将 S h l S_{h_l} Shl缩写为 S l S_l Sl。网格 { S 1 , . . , S L } \left \{S_1,..,S_L\right \} {S1,..,SL}被叫做S的多重网格。如果一个粗网络 S l S_l Sl属于一个细网络 S l + 1 S_{l+1} Sl+1,则称 S l S_l Sl嵌套于 S l + 1 S_{l+1} Sl+1。嵌套网格可以在计算过程中带来方便,因为从粗网格映射到细网格时不需要额外的计算成本。
在各层网格 S l S_l Sl上,将原优化问题(5)简化为离散优化问题:
a r g m i n f ( x ) , x ∈ S l , l = 1 , . . . , L argminf(x),x\in S_l,l=1,...,L argminf(x),x∈Sl,l=1,...,L
由于 S l S_l Sl是一个有限的集合,因此在网格 S l S_l Sl上一定存在一个最小值点 x l ∗ ∈ S l x_l^*\in S_l xl∗∈Sl。
2.2算法步骤
定义L为最大的层数,K为最大的迭代次数。定义第l层的第k次迭代种群为 ϕ l k = x 1 , . . . , x N \phi _l^{k}={x_1,...,x_N} ϕlk=x1,...,xN,MEA被表述如下:
Input:编码长度,定义域,迭代次数,种群大小, σ \sigma σ初始化值,网格层数L,网格大小更新率H;
output:最优种群
begin
ϕ 1 : = \phi_1:= ϕ1:=随机初始化,初始化 h 1 = 0.01 ( b i − a i ) h_1=0.01(b_i-a_i) h1=0.01(bi−ai), b i , a i b_i,a_i bi,ai是定义域的界;
for(l=1 to L)do
ϕ l ( 0 ) : = ϕ l \phi_l^{(0)}:=\phi_l ϕl(0):=ϕl;
for(k=0 to K-1)do
ϕ l ( k + 1 / 3 ) : = m u t a t i o n ( ϕ l ( k ) ) \phi_l^{(k+1/3)}:=mutation(\phi_l^{(k)}) ϕl(k+1/3):=mutation(ϕl(k));
ϕ l ( k + 2 / 3 ) : = r e s t r i c t i o n ( ϕ l ( k ) ) \phi_l^{(k+2/3)}:=restriction(\phi_l^{(k)}) ϕl(k+2/3):=restriction(ϕl(k));
ϕ l ( k + 1 ) : = s e l e c t ( ϕ l ( k ) , ϕ l ( k + 2 / 3 ) ) \phi_l^{(k+1)}:=select(\phi_l^{(k)},\phi_l^{(k+2/3)}) ϕl(k+1):=select(ϕl(k),ϕl(k+2/3));
end
ϕ l + 1 : = r e s t r i c t i o n ( ϕ l ( K ) ) \phi_{l+1}:=restriction(\phi_l^{(K)}) ϕl+1:=restriction(ϕl(K));
h l + 1 = h l / H h_{l+1}=h_l/H hl+1=hl/H;
end
输出结果。
end
(1) 表示:这里一个种群由N个个体随机组成,每个个体表示为一组实数向量 ( x i ⃗ , σ i ⃗ ) (\vec{x_i},\vec{\sigma_i}) (xi,σi),
x i ⃗ = ( x i ( 1 ) , x i ( 2 ) , . . . , x i ( n ) ) ; σ i ⃗ = ( σ i ( 1 ) , σ i ( 2 ) , . . . , σ i ( n ) ) , i = 1 , . . . , N \vec{x_i}=(x_i(1),x_i(2),...,x_i(n));\vec{\sigma_i}=(\sigma_i(1),\sigma_i(2),...,\sigma_i(n)),i=1,...,N xi=(xi(1),xi(2),...,xi(n));σi=(σi(1),σi(2),...,σi(n)),i=1,...,N
这里的 σ \sigma σ初始化为给定的一个值。
(2)变异:此处采用经典的高斯变异。对于每一个父代,以如下规则产生一个子代,
σ i ′ ( j ) = σ i ( j ) e x p τ N ( 0 , 1 ) + τ ′ N j ( 0 , 1 ) , j = 1 , . . . , n x i ′ ( j ) = x i ( j ) + σ i ′ ( j ) N j ( 0 , 1 ) , j = 1 , . . . , n \begin{matrix} \sigma_i^{'}(j)=\sigma_i(j)exp^{\tau N(0,1)+\tau^{'}N_j(0,1)},j=1,...,n \\ x_i^{'}(j)=x_i(j)+\sigma_i^{'}(j)N_j(0,1),j=1,...,n \end{matrix} σi′(j)=σi(j)expτN(0,1)+τ′Nj(0,1),j=1,...,nxi′(j)=xi(j)+σi′(j)Nj(0,1),j=1,...,n
这里 N ( 0 , 1 ) N(0,1) N(0,1)是为每个i产生一个标准的正态分布值, N j ( 0 , 1 ) N_j(0,1) Nj(0,1)是为每个j产生一个标准的正态分布值, τ = 1 / 2 N \tau=1/\sqrt{2N} τ=1/2N, τ ′ = 1 / 2 N \tau^{'}=1/\sqrt{2\sqrt{N}} τ′=1/2N。
(3)选择:这里从父代加子代中选择N个个体,采用五元竞标赛。
(4)限制:为了保证所取点在网格上,对于每个产生的子代x,做如下限制得到新的子代: x = ⌊ x / h ⌋ h x=\left \lfloor x/h \right \rfloor h x=⌊x/h⌋h。
说明:这里不止可以使用变异算子,交叉算子也可加入到内循环,为了和FEP保持一致,此次实验并未使用交叉算子。
3.the fast EP
3.1 简介
Evolutionary programming (EP)成功的运用在数值计算里,经典的进化规划(CEP)使用的高斯变异,其收敛速度较慢,而快速进化规划(FEP)使用柯西变异代替高斯变异,加快了收敛速度。[3]中已证明FEP在大领域搜索范围内表现得好,CEP在小领域内表现得好,并且提出了改进的算法IFEP。IFEP其实只是在FEP的基础上,对产生变异部分进行了修改:即一个父代分别通过高斯变异和柯西变异产生两个候选子代,选取适应度高的最为真正的子代。此次实验采用的FEP。
3.2 算法步骤
定义K为最大的迭代次数。定义第k次迭代种群为 ϕ k = x 1 , . . . , x N \phi _{k}={x_1,...,x_N} ϕk=x1,...,xN,FEP被表述如下:
Input:编码长度,定义域,迭代次数,种群大小, σ \sigma σ初始化值;
output:最优种群
begin
ϕ 0 : = \phi_0:= ϕ0:=随机初始化;
for(k=0 to K-1)do
ϕ k ′ : = m u t a t i o n ( ϕ k ) \phi_{k}^{'}:=mutation(\phi_{k}) ϕk′:=mutation(ϕk);
ϕ k + 1 : = s e l e c t ( ϕ k ′ , ϕ k ) \phi_{k+1}:=select(\phi_{k}^{'},\phi_{k}) ϕk+1:=select(ϕk′,ϕk);
end
输出结果。
end
(1) 表示:这里一个种群由N个个体随机组成,每个个体表示为一组实数向量 ( x i ⃗ , σ i ⃗ ) (\vec{x_i},\vec{\sigma_i}) (xi,σi),
x i ⃗ = ( x i ( 1 ) , x i ( 2 ) , . . . , x i ( n ) ) ; σ i ⃗ = ( σ i ( 1 ) , σ i ( 2 ) , . . . , σ i ( n ) ) , i = 1 , . . . , N \vec{x_i}=(x_i(1),x_i(2),...,x_i(n));\vec{\sigma_i}=(\sigma_i(1),\sigma_i(2),...,\sigma_i(n)),i=1,...,N xi=(xi(1),xi(2),...,xi(n));σi=(σi(1),σi(2),...,σi(n)),i=1,...,N
这里的 σ \sigma σ初始化为输入的一个定值。
(2)变异:此处采用的柯西变异。对于每一个父代,以如下规则产生一个子代,
σ i ′ ( j ) = σ i ( j ) e x p τ C ( 0 , 1 ) + τ ′ C j ( 0 , 1 ) , j = 1 , . . . , n x i ′ ( j ) = x i ( j ) + σ i ′ ( j ) C j ( 0 , 1 ) , j = 1 , . . . , n \begin{matrix} \sigma_i^{'}(j)=\sigma_i(j)exp^{\tau C(0,1)+\tau^{'}C_j(0,1)},j=1,...,n \\ x_i^{'}(j)=x_i(j)+\sigma_i^{'}(j)C_j(0,1),j=1,...,n \end{matrix} σi′(j)=σi(j)expτC(0,1)+τ′Cj(0,1),j=1,...,nxi′(j)=xi(j)+σi′(j)Cj(0,1),j=1,...,n
这里 C ( 0 , 1 ) C(0,1) C(0,1)是为每个i产生一个标准的柯西分布值, C j ( 0 , 1 ) C_j(0,1) Cj(0,1)是为每个j产生一个标准的柯西分布值, τ = 1 / 2 N \tau=1/\sqrt{2N} τ=1/2N, τ ′ = 1 / 2 N \tau^{'}=1/\sqrt{2\sqrt{N}} τ′=1/2N。
(3)选择:这里从父代加子代中选择N个个体,采用十元竞标赛。
4.实验
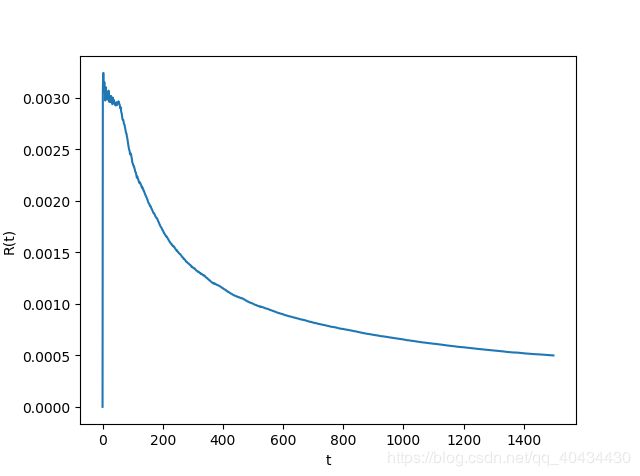
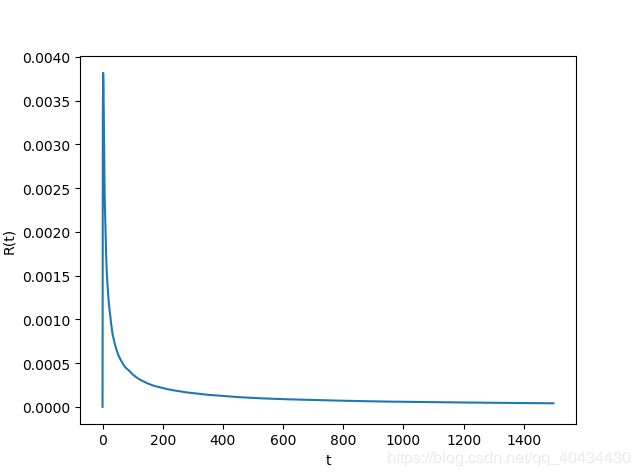
Ackley’s function自变量个数设置为30,种群大小设置为100,MEA的网格层数L设置为15,网格更新率设置为3,每层迭代次数位100,FEP的迭代次数设置为1500, σ \sigma σ初始化为3.0。每个算法运行100次,计算R(t)得到结果如图1,2所示。
观察图1和图2,平均收敛速率都趋于平稳,说明此指标存在一个界。
python代码
python代码借鉴了部分莫烦python的内容(https://morvanzhou.github.io/),在此鸣谢。
FEP在OneMax问题上的python代码(python3.6):
import numpy as np
import matplotlib.pyplot as plt
import math
import copy
#参数设置
DNA_SIZE = 30 # DNA实数编码长度
DNA_BOUND = [-32-math.exp(1), 32-math.exp(1)] # 解的上下界
N_GENERATIONS = 1500 # 迭代次数
POP_SIZE = 100 # 种群大小
t1 = (1/(2*POP_SIZE))**0.5 #变异参数t1
t2 = (1/(2*(POP_SIZE**0.5)))**0.5 #变异参数t2
tur = 10 #十元锦标赛
TIME = 100 #实验次数
bestfitness=np.zeros((N_GENERATIONS,TIME)) #储存每代最优解
fopt = 0 #最优解值
mu = 3 #sigma初始化
#目标函数值计算
def F(x):
f = -20*np.exp(-0.2*((np.sum((x+math.exp(1))**2,axis=1)/x.shape[1])**0.5)) - np.exp((np.sum(np.cos(2*np.pi*x+2*np.pi*np.exp(1)),axis=1))/x.shape[1]) + 20 + math.exp(1)
return f
#变异算子
def mutation(pop):
# 产生子代
pop1 = copy.deepcopy(pop)
for d, s in zip(pop1['DNA'], pop1['sigma']):
#变异
temp = np.random.randn()
temp1 = np.random.randn(*s.shape)
#s[:] = np.maximum(s*np.exp(t1*temp+t2*temp1),0)
s[:] = s*np.exp(t1*temp+t2*temp1)
#s[:] = np.maximum(s + (np.random.rand(*s.shape)-0.5), 0.) # must > 0
d += s * np.random.standard_cauchy(*d.shape)
# tempp=np.random.uniform(DNA_BOUND[0], DNA_BOUND[1], *d.shape)
# d += s * tempp
d[:] = np.clip(d, *DNA_BOUND) # 防止越界
return pop1
#选择算子
def select(pop,pop1,ind1,ind2):
for key in ['DNA', 'sigma']:
pop[key] = np.vstack((pop[key], pop1[key]))
############################################锦标赛选择
idx = np.random.randint(0, high=2*POP_SIZE, size=(POP_SIZE*tur))
fitness = F(pop['DNA'][idx]) # 计算适应度函数
fitness = fitness.reshape(POP_SIZE,tur)
fitnessmin = fitness.argmin(axis=1)
good_idx = idx[np.arange(POP_SIZE)*tur+fitnessmin]
temp=get_fitness(F(pop['DNA'][good_idx]))
temp.sort(axis = 0)
bestfitness[ind1][ind2]=temp[0]
############################################轮盘赌选择
# fitness = get_fitness(F(pop['DNA'])) # 计算适应度函数
# good_idx = np.random.choice(np.arange(2*POP_SIZE), size=POP_SIZE, replace=True, p=fitness/fitness.sum())#轮盘赌
# temp=get_fitness(F(pop['DNA'][good_idx]))
# temp.sort(axis = 0)
# bestfitness[ind1][ind2]=temp[0]
############################################适应度等级选择
# fitness = get_fitness(F(pop['DNA'])) # 计算适应度函数
# idx = np.arange(pop['DNA'].shape[0])
# good_idx = idx[fitness.argsort()][:POP_SIZE] # 通过适应度等级选择(因为是最小化问题,越小越好)
# bestfitness[ind1][ind2]=fitness[good_idx[0]]
################################################
for key in ['DNA', 'sigma']:
pop[key] = pop[key][good_idx]
return pop
# 找到非零的函数值用于选择
def get_fitness(pred): return pred.flatten()
###############################################################################
for st in range(TIME):
#种群初始化
#pop = dict(DNA=DNA_BOUND[0]+(DNA_BOUND[1]-DNA_BOUND[0])*np.random.rand(POP_SIZE,DNA_SIZE),sigma=np.random.rand(POP_SIZE,DNA_SIZE))#种群初始化以及sigma初始化
pop = dict(DNA=DNA_BOUND[0]+(DNA_BOUND[1]-DNA_BOUND[0])*np.random.rand(POP_SIZE,DNA_SIZE),sigma=mu*np.ones([POP_SIZE,DNA_SIZE]))#种群初始化以及sigma初始化
#迭代过程
for j in range(N_GENERATIONS):
print("第{name3}次实验的第{name2}次迭代".format(name3=st,name2=j))
pop1 = mutation(pop)
pop = select(pop,pop1,j,st)
ft=np.mean(bestfitness, axis=1)#求适应度均值
RT=ft.copy()
for i in range(RT.shape[0]):
if i==0:
RT[0]=0
else:
if ft[0]==0:
RT[i] = 1
else:
RT[i]=1-(abs(fopt-ft[i])/abs(fopt-ft[0]))**(1/i)
#画出收敛曲线
plt.figure(1)
plt.plot(RT)
plt.xlabel('t')
plt.ylabel('R(t)')
plt.show()
##画随着平均迭代次数f值的变化
plt.figure(2)
plt.plot(ft)
plt.xlabel('t')
plt.ylabel('bestfitness')
plt.show()
MEA在OneMax问题上的python代码(python3.6):
import numpy as np
import matplotlib.pyplot as plt
import math
import copy
#参数设置
DNA_SIZE = 30 # DNA实数编码长度
DNA_BOUND = [-32-math.exp(1), 32-math.exp(1)] # 解的上下界
N_GENERATIONS = 100 # 迭代次数
POP_SIZE = 100 # 种群大小
L = 15 #网格层数
H = np.zeros(L) #网格大小
H[0] = 0.01*(DNA_BOUND[1]-DNA_BOUND[0]) #初始网格大小
GR = 3 #网格增长率
t1 = (1/(2*POP_SIZE))**0.5 #变异参数t1
t2 = (1/(2*(POP_SIZE**0.5)))**0.5 #变异参数t2
tur = 5 #五元锦标赛
TIME = 100 #实验次数
bestfitness=np.zeros((N_GENERATIONS*L,TIME)) #储存每代最优解
fopt = 0 #最优解值
mu = 3 #sigma初始化
#目标函数值计算
def F(x):
f = -20*np.exp(-0.2*((np.sum((x+math.exp(1))**2,axis=1)/x.shape[1])**0.5)) - np.exp((np.sum(np.cos(2*np.pi*x+2*np.pi*np.exp(1)),axis=1))/x.shape[1]) + 20 + math.exp(1)
return f
#变异算子
def mutation(pop):
# 产生子代
pop1 = copy.deepcopy(pop)
for d, s in zip(pop1['DNA'], pop1['sigma']):
#变异
temp = np.random.randn()
temp1 = np.random.randn(*s.shape)
#s[:] = np.maximum(s*np.exp(t1*temp+t2*temp1),0)
s[:] = s*np.exp(t1*temp+t2*temp1)
#s[:] = np.maximum(s + (np.random.rand(*s.shape)-0.5), 0.) # must > 0
d += s * np.random.randn(*d.shape)
# tempp=np.random.uniform(DNA_BOUND[0], DNA_BOUND[1], *d.shape)
# d += s * tempp
d[:] = np.clip(d, *DNA_BOUND) # 防止越界
return pop1
#限制算子
def restriction(pops,h):
for d in pops['DNA']:
d = np.floor(d/h)*h
d[:] = np.clip(d, *DNA_BOUND) # 防止越界
#pops['DNA'] = np.floor(pops['DNA']/h)*h
return pops
#选择算子
def select(pop,pop1,ind1,ind2,ind3):
for key in ['DNA', 'sigma']:
pop[key] = np.vstack((pop[key], pop1[key]))
############################################锦标赛选择
idx = np.random.randint(0, high=2*POP_SIZE, size=(POP_SIZE*tur))
fitness = F(pop['DNA'][idx]) # 计算适应度函数
fitness = fitness.reshape(POP_SIZE,tur)
fitnessmin = fitness.argmin(axis=1)
good_idx = idx[np.arange(POP_SIZE)*tur+fitnessmin]
temp=get_fitness(F(pop['DNA'][good_idx]))
temp.sort(axis = 0)
bestfitness[ind1*N_GENERATIONS+ind2][ind3]=temp[0]
############################################轮盘赌选择
# fitness = get_fitness(F(pop['DNA'])) # 计算适应度函数
# good_idx = np.random.choice(np.arange(2*POP_SIZE), size=POP_SIZE, replace=True, p=fitness/fitness.sum())#轮盘赌
# temp=get_fitness(F(pop['DNA'][good_idx]))
# temp.sort(axis = 0)
# bestfitness[ind1*N_GENERATIONS+ind2][0]=temp[0]
############################################适应度等级选择
# fitness = get_fitness(F(pop['DNA'])) # 计算适应度函数
# idx = np.arange(pop['DNA'].shape[0])
# good_idx = idx[fitness.argsort()][:POP_SIZE] # 通过适应度等级选择(因为是最小化问题,越小越好)
# bestfitness[ind1*N_GENERATIONS+ind2][0]=fitness[good_idx[0]]
################################################
for key in ['DNA', 'sigma']:
pop[key] = pop[key][good_idx]
return pop
# 找到非零的函数值用于选择
def get_fitness(pred): return pred.flatten()
###############################################################################
for st in range(TIME):
#种群初始化
#pop = dict(DNA=DNA_BOUND[0]+(DNA_BOUND[1]-DNA_BOUND[0])*np.random.rand(POP_SIZE,DNA_SIZE),sigma=np.random.rand(POP_SIZE,DNA_SIZE))#种群初始化以及sigma初始化
pop = dict(DNA=DNA_BOUND[0]+(DNA_BOUND[1]-DNA_BOUND[0])*np.random.rand(POP_SIZE,DNA_SIZE),sigma=mu*np.ones([POP_SIZE,DNA_SIZE]))#种群初始化以及sigma初始化
#迭代过程
for i in range(L):
for j in range(N_GENERATIONS):
print("第{name3}次实验第{name}层网格的第{name2}次迭代".format(name3=st,name=i,name2=j))
pop1 = mutation(pop)
Hh = H[i]
pop1 = restriction(pop1,Hh)
pop = select(pop,pop1,i,j,st)
pop = restriction(pop,Hh)
if(i+1 == L):
break
H[i+1] = H[i]/GR
ft=np.mean(bestfitness, axis=1)#求适应度均值
RT=ft.copy()
for i in range(RT.shape[0]):
if i==0:
RT[0]=0
else:
if ft[0]==0:
RT[i] = 1
else:
RT[i]=1-(abs(fopt-ft[i])/abs(fopt-ft[0]))**(1/i)
#画出收敛曲线
plt.figure(1)
plt.plot(RT)
plt.xlabel('t')
plt.ylabel('R(t)')
plt.show()
##画随着平均迭代次数f值的变化
plt.figure(2)
plt.plot(ft)
plt.xlabel('t')
plt.ylabel('bestfitness')
plt.show()
IV 离散优化问题的平均收敛速率
以下分析离散优化问题的EAs,并且假设算法的遗传算子在进化过程中是不变的,将EA建模成一个齐次马尔科夫链,其转换概率如下: P r ( X , Y ) : = P r ( ϕ t + 1 = Y ∣ ϕ t = X ) Pr(X,Y):=Pr(\phi_{t+1}=Y|\phi_{t}=X) Pr(X,Y):=Pr(ϕt+1=Y∣ϕt=X), X , Y ∈ S X,Y\in S X,Y∈S。定义P为含有 P r ( X , Y ) Pr(X,Y) Pr(X,Y)转换矩阵。如果一个种群包含一个最优解,那么称这个种群是最优的;否则为非优的。令 S o p t S_{opt} Sopt为一组最优种群的集合,那么 S n o n = S ∖ S o p t S_{non}=S\setminus S_{opt} Snon=S∖Sopt。设定停止准则,最优集合总是吸收的,即 P r ( ϕ t + 1 ∈ S n o n ∣ ϕ t ∈ S o p t ) = 0 Pr(\phi_{t+1}\in S_{non}|\phi_{t}\in S_{opt})=0 Pr(ϕt+1∈Snon∣ϕt∈Sopt)=0。那么转换矩阵P为
P = ( A O B Q ) P=\begin{pmatrix} A & O\\ B & Q \end{pmatrix} P=(ABOQ)
这里***A***是代表从最优状态到最优的一个转换概率子矩阵;***O***是代表从最优状态到非优的一个转换概率子矩阵,其全部元素为0;***B***是从非优状态到最优的一个转换概率子矩阵;***Q***是一个非优到非优的转换概率子矩阵。
因为 ϕ t \phi_{t} ϕt是一个随机变量,那么我们自然研究其概率分布。令 q t ( X ) q_t(X) qt(X)为非优状态**X的的概率,即 q t ( X ) : = P r ( ϕ t = X ) q_t(X):=Pr(\phi_t=X) qt(X):=Pr(ϕt=X)。令向量 ( X 1 , X 2 , . . . ) (X_1,X_2,...) (X1,X2,...)代表所有非最优状态,向量 q t T q_t^T qtT定义为在非最优集合中 ϕ t \phi_{t} ϕt的概率分布,这里 q t : = ( q t ( X 1 ) , q t ( X 2 ) , . . . ) T q_t:=(q_t(X_1),q_t(X_2),...)^T qt:=(qt(X1),qt(X2),...)T。对于一个初始的概率分布, q 0 ≥ 0 q_0\geq0 q0≥0,这里0= ( 0 , 0 , . . . ) T (0,0,...)^T (0,0,...)T,并且只有初始种群从最优解集合中选择, q 0 q_0 q0才为0。
只考虑非最优状态之间的概率转移,它可以用如下矩阵迭代表示: q t T = q t − 1 T Q = q 0 T Q t q^T_t=q^T_{t-1}Q=q_0^TQ^t qtT=qt−1TQ=q0TQt。
当对于任意 q 0 , l i m t → ∞ q t = 0 , o r , l i m t → + ∞ Q t = O q_0,lim_{t\rightarrow\infty}q_t=0 ,or,lim_{t\rightarrow+\infty}Q^t=O q0,limt→∞qt=0,or,limt→+∞Qt=O,则称一个进化算法是收敛的。 f t f_t ft适应度值的期望为 f t : = E [ f ( ϕ t ) ] = ∑ X ∈ S f ( X ) P r ( ϕ t = X ) f_t:=E[f(\phi_t)]=\sum_{X\in S}f(X)Pr(\phi_t=X) ft:=E[f(ϕt)]=∑X∈Sf(X)Pr(ϕt=X)。那么 f o p t − f t = ∑ X ∈ S n o n ( f ( X ) − f o p t ) q t ( X ) f_{opt}-f_t=\sum_{X\in S_{non}}(f(X)-f_{opt})q_t(X) fopt−ft=∑X∈Snon(f(X)−fopt)qt(X)。
令向量 f : = ( f ( X 1 ) , f ( X 2 ) , . . . ) T f:=(f(X_1),f(X_2),...)^T f:=(f(X1),f(X2),...)T为所有非优种群的适应度值,那么
f o p t − f t = q t T ⋅ ( f o p t 1 − f ) f_{opt}-f_t=q_t^T\cdot(f_{opt}1-f) fopt−ft=qtT⋅(fopt1−f)
这里的 1 = ( 1 , 1... ) T 1=(1,1...)^T 1=(1,1...)T。对于一个向量V,定义 ∣ ∣ v T ∣ ∣ : = ∣ v T ⋅ ( f o p t 1 − f ) ∣ ||v^T||:=|v^T\cdot(f_{opt}1-f)| ∣∣vT∣∣:=∣vT⋅(fopt1−f)∣。因为当且仅当v=0, ∣ ∣ v ∣ ∣ = 0 ||v||=0 ∣∣v∣∣=0; ∣ ∣ a v ∣ ∣ = ∣ a ∣ ∥ v ∥ ||av||=\left | a \right | \left \| v \right \| ∣∣av∣∣=∣a∣∥v∥并且 ∣ ∣ v 1 + v 2 ∣ ∣ ≥ ∥ v 1 ∥ ∥ v 2 ∥ ||v_1+v_2||\geq\left \| v_1 \right \|\left \| v_2 \right \| ∣∣v1+v2∣∣≥∥v1∥∥v2∥,那么$ \left | v \right | 是 一 个 向 量 范 数 。 对 于 一 个 矩 阵 ∗ ∗ M ∗ ∗ , 令 是一个向量范数。对于一个矩阵**M**,令 是一个向量范数。对于一个矩阵∗∗M∗∗,令 \left | M \right |$为
∥ M ∥ = s u p { ∥ v T M ∥ ∥ v T ∥ : v ≠ 0 } \left \| M \right \|=sup\left \{ \frac{\left \| v^TM \right \|}{\left \| v^T \right \|}:v\neq0 \right \} ∥M∥=sup{∥vT∥∥∥vTM∥∥:v̸=0}
根据上述马尔科夫链模型,评估平均收敛速率的下界如定理1。
定理1:令Q为收敛EA的一个转换子矩阵,对于任何的 q 0 ≠ 0 q_0\neq 0 q0̸=0有以下结论成立:
1)t代平均收敛速率的下界为
R ( t ) ≥ 1 − ∥ Q t ∥ 1 / t R(t)\geq1-\left \| Q^t \right \|^{1/t} R(t)≥1−∥∥Qt∥∥1/t
2)t代的平均收敛速率的极限为
l i m t → + ∞ R ( t ) ≥ 1 − ρ ( Q ) lim_{t\rightarrow+\infty}R(t)\geq1-\rho(Q) limt→+∞R(t)≥1−ρ(Q)
3)在随机初始化下(对于任何的 X ∈ S n o n X\in S_{non} X∈Snon或者 q 0 > 0 q_0>0 q0>0, P r ( ϕ 0 = X ) > 0 Pr(\phi_0=X)>0 Pr(ϕ0=X)>0),则
l i m t → + ∞ R ( t ) = 1 − ρ ( Q ) lim_{t\rightarrow+\infty}R(t)=1-\rho(Q) limt→+∞R(t)=1−ρ(Q)
4)在特定的初始化下(设置 q 0 = v / ∣ v ∣ q_0=v/ |v| q0=v/∣v∣,这里v是特征值 ρ ( Q ) \rho(Q) ρ(Q)相应的特征向量,这里 v ≥ 0 v\geq0 v≥0但 v ≠ 0 v\neq0 v̸=0),则对于所有的 t ≥ 1 t\geq 1 t≥1
R ( t ) = 1 − ρ ( Q ) R(t)=1-\rho(Q) R(t)=1−ρ(Q)
证明:
1)由于 q t T = q 0 T Q t q_t^T=q_0^TQ^t qtT=q0TQt,则
∣ f o p t − f t f o p t − f 0 ∣ = ∥ q t T ∥ ∥ q 0 T ∥ = ∥ q 0 T Q t ∥ ∥ q 0 T ∥ ≤ ∥ q 0 T ∥ ∥ Q t ∥ ∥ q 0 T ∥ = ∥ Q t ∥ |\frac{f_{opt}-f_t}{f_{opt}-f_{0}}|=\frac{\left \| q_t^T \right \|}{\left \| q_0^T \right \|}=\frac{\left \| q_0^TQ^t \right \|}{\left \| q_0^T \right \|}\leq\frac{\left \| q_0^T \right \|\left \| Q^t \right \|}{\left \| q_0^T \right \|}=\left \| Q^t \right \| ∣fopt−f0fopt−ft∣=∥∥q0T∥∥∥∥qtT∥∥=∥∥q0T∥∥∥∥q0TQt∥∥≤∥∥q0T∥∥∥∥q0T∥∥∥Qt∥=∥∥Qt∥∥
因此(14)成立。
2)根据Gelfand’s spectral radius定理,得
l i m t → + ∞ ∥ Q t ∥ 1 / t = ρ ( Q ) lim_{t\rightarrow+\infty}\left \| Q^t \right \|^{1/t}=\rho(Q) limt→+∞∥∥Qt∥∥1/t=ρ(Q)
因此(15)成立。
3)因为 Q ≥ 0 Q\geq0 Q≥0,根据Perron–Frobenius定理, ρ ( Q ) \rho(Q) ρ(Q)是Q的特征值。存在一个相应于 ρ ( Q ) \rho(Q) ρ(Q)特征向量v使得 v ≥ 0 v\geq0 v≥0但 v ≠ 0 v\neq0 v̸=0。特别的
ρ ( Q ) v T = v T Q \rho(Q)v^T=v^TQ ρ(Q)vT=vTQ
令max(v)为向量v的元素中最大值。由于随机初始化, q 0 > 0 q_0>0 q0>0。令 m i n ( q 0 ) min(q_0) min(q0)为向量 q 0 q_0 q0的元素中最小值,设
u = m i n ( q 0 ) m a x ( v ) v u=\frac{min(q_0)}{max(v)}v u=max(v)min(q0)v
则
ρ ( Q ) u T = u T Q \rho(Q)u^T=u^TQ ρ(Q)uT=uTQ
这里的向量u**是 ρ ( Q ) \rho(Q) ρ(Q)的一个特征向量。令 w = q 0 − u w=q_0-u w=q0−u。那么根据(21),我们有 w ≥ 0 w\geq0 w≥0。因此 q 0 = u + w , w ≥ 0 , Q ≥ 0 q_0=u+w,w\geq0,Q\geq0 q0=u+w,w≥0,Q≥0,则
q t T = q 0 T Q t = ( u + w ) T Q t ≥ u T Q t = ρ ( Q ) t u T q_t^T=q_0^TQ^t=(u+w)^TQ^t\geq u^TQ^t=\rho(Q)^tu^T qtT=q0TQt=(u+w)TQt≥uTQt=ρ(Q)tuT
则
∣ f o p t − f t f o p t − f 0 ∣ = ∣ q t T ⋅ ( f o p t 1 − f ) f o p t − f 0 ∣ ≥ ∣ ρ ( Q ) t u T ⋅ ( f o p t 1 − f ) q 0 T ⋅ ( f o p t 1 − f ) ∣ |\frac{f_{opt}-f_t}{f_{opt}-f_{0}}|=|\frac{q_t^T\cdot(f_{opt}1-f)}{f_{opt}-f_{0}}|\geq|\frac{\rho(Q)^tu^T\cdot(f_{opt}1-f)}{q_0^T\cdot(f_{opt}1-f)}| ∣fopt−f0fopt−ft∣=∣fopt−f0qtT⋅(fopt1−f)∣≥∣q0T⋅(fopt1−f)ρ(Q)tuT⋅(fopt1−f)∣
∣ f o p t − f t f o p t − f 0 ∣ 1 / t ≥ ρ ( Q ) ∣ u T ⋅ ( f o p t 1 − f ) q 0 T ⋅ ( f o p t 1 − f ) ∣ 1 / t |\frac{f_{opt}-f_t}{f_{opt}-f_{0}}|^{1/t}\geq\rho(Q)|\frac{u^T\cdot(f_{opt}1-f)}{q_0^T\cdot(f_{opt}1-f)}|^{1/t} ∣fopt−f0fopt−ft∣1/t≥ρ(Q)∣q0T⋅(fopt1−f)uT⋅(fopt1−f)∣1/t
由于 u T ⋅ ( f o p t 1 − f ) u^T\cdot(f_{opt}1-f) uT⋅(fopt1−f)和 q 0 T ⋅ ( f o p t 1 − f ) q_0^T\cdot(f_{opt}1-f) q0T⋅(fopt1−f)不受t的约束,因此
l i m t → + ∞ ∣ u T ⋅ ( f o p t 1 − f ) q 0 T ⋅ ( f o p t 1 − f ) ∣ 1 / t = 1 lim_{t\rightarrow+\infty}|\frac{u^T\cdot(f_{opt}1-f)}{q_0^T\cdot(f_{opt}1-f)}|^{1/t}=1 limt→+∞∣q0T⋅(fopt1−f)uT⋅(fopt1−f)∣1/t=1
则
l i m t → + ∞ ∣ f o p t − f t f o p t − f 0 ∣ 1 / t ≥ ρ ( Q ) lim_{t\rightarrow+\infty}|\frac{f_{opt}-f_t}{f_{opt}-f_{0}}|^{1/t}\geq \rho(Q) limt→+∞∣fopt−f0fopt−ft∣1/t≥ρ(Q)
l i m t → + ∞ R ( t ) = 1 − l i m t → + ∞ ∣ f o p t − f t f o p t − f 0 ∣ 1 / t ≤ 1 − ρ ( Q ) lim_{t\rightarrow+\infty}R(t)=1-lim_{t\rightarrow+\infty}|\frac{f_{opt}-f_t}{f_{opt}-f_{0}}|^{1/t}\leq1-\rho(Q) limt→+∞R(t)=1−limt→+∞∣fopt−f0fopt−ft∣1/t≤1−ρ(Q)
4)设置 q 0 = v / ∑ i v i q_0=v/\sum_{i}v_i q0=v/∑ivi。v在步骤3中给出。这里的向量 q 0 q_0 q0是 ρ ( Q ) \rho(Q) ρ(Q)的一个特征向量则 ρ ( Q ) q 0 T = q 0 T Q \rho(Q)q_0^T=q_0^TQ ρ(Q)q0T=q0TQ。由于 q t T = q t − 1 T Q q_t^T=q_{t-1}^TQ qtT=qt−1TQ,则
f o p t − f t f o p t − f 0 = q t T ⋅ ( f o p t 1 − f ) f o p t − f 0 = ρ ( Q ) t q 0 T ⋅ ( f o p t 1 − f ) q 0 T ⋅ ( f o p t 1 − f ) \frac{f_{opt}-f_t}{f_{opt}-f_{0}}=\frac{q_t^T\cdot(f_{opt}1-f)}{f_{opt}-f_{0}}=\frac{\rho(Q)^tq_0^T\cdot(f_{opt}1-f)}{q_0^T\cdot(f_{opt}1-f)} fopt−f0fopt−ft=fopt−f0qtT⋅(fopt1−f)=q0T⋅(fopt1−f)ρ(Q)tq0T⋅(fopt1−f)
那么,对于任何 t ≥ 1 t\geq1 t≥1
f o p t − f t f o p t − f 0 ∣ 1 / t = ρ ( Q ) \frac{f_{opt}-f_t}{f_{opt}-f_{0}}|^{1/t}=\rho(Q) fopt−f0fopt−ft∣1/t=ρ(Q)
则(17)成立。
综上,我们称 1 − ρ ( Q ) 1-\rho(Q) 1−ρ(Q)为EA的渐进平均收敛速率,记为 R ∞ R_{\infty} R∞。
V 渐进平均收敛率和击中时间
1.击中时间和渐进平均收敛率的关系
期望击中时间是指找到一个最优解的总代数。它与渐进平均收敛率有一些联系。假设 m ( X ) m(X) m(X)是一个收敛的EA从状态***X***开始命中 S o p t S_{opt} Sopt的期望代数。定义 m : = ( m ( X 1 ) , m ( X 2 ) , . . . ) m:=(m(X_1),m(X_2),...) m:=(m(X1),m(X2),...),这里 ( X 1 X 2 , . . . ) (X_1X_2,...) (X1X2,...)代表所有非优状态。
定理2:设Q为与收敛EA相关的转换子矩阵。那么 1 / R ∞ 1/R_{\infty} 1/R∞不超过 ∥ m ∥ ∞ : = m a x { m ( X ) ; X ∈ S n o n } \left \| m \right \|_{\infty}:=max\left \{ m(X);X\in S_{non} \right \} ∥m∥∞:=max{m(X);X∈Snon}。
证明:根据基本矩阵定理[5, Th. 11.5], m = ( I − Q ) − 1 1 m=(I-Q)^{-1}1 m=(I−Q)−11。这里 I I I是一个单位阵。那么
∥ m ∥ ∞ = ∥ ( I − Q ) − 1 1 ∥ ∞ = ∥ ( I − Q ) − 1 ∥ ∞ ≥ ρ ( ( I − Q ) − 1 ) = ( 1 − ρ ( Q ) ) − 1 \left \| m \right \|_{\infty}=\left \| (I-Q)^{-1}1 \right \|_{\infty}=\left \| (I-Q)^{-1} \right \|_{\infty}\geq\rho((I-Q)^{-1})=(1-\rho(Q))^{-1} ∥m∥∞=∥∥(I−Q)−11∥∥∞=∥∥(I−Q)−1∥∥∞≥ρ((I−Q)−1)=(1−ρ(Q))−1
这里最后一个等式基于 ( 1 − ρ ( Q ) ) − 1 (1-\rho(Q))^{-1} (1−ρ(Q))−1是 ( I − Q ) − 1 (I-Q)^{-1} (I−Q)−1的特征值和谱半径。易知, 1 / R ∞ 1/R_{\infty} 1/R∞是期望运行时间的一个下界。
推论1:设Q为与收敛EA相关的转换子矩阵。
3)在随机初始化下( q 0 > 0 q_0>0 q0>0),则
l i m t → + ∞ ∣ f o p t − f t ∣ 1 / t ρ ( Q ) ∣ f o p t − f 0 ∣ 1 / t = 1 lim_{t\rightarrow+\infty}\frac{|f_{opt}-f_t|^{1/t}}{\rho(Q)|f_{opt}-f_{0}|^{1/t}}=1 limt→+∞ρ(Q)∣fopt−f0∣1/t∣fopt−ft∣1/t=1
4)在特定的初始化下(设置 q 0 = v / ∣ v ∣ q_0=v/ |v| q0=v/∣v∣,这里v是特征值 ρ ( Q ) \rho(Q) ρ(Q)相应的特征向量,这里 v ≥ 0 v\geq0 v≥0但 v ≠ 0 v\neq0 v̸=0),则对于所有 t ≥ 1 t\geq 1 t≥1
∣ f o p t − f t ∣ ρ ( Q ) t ∣ f o p t − f 0 ∣ = 1 \frac{|f_{opt}-f_t|}{\rho(Q)^t|f_{opt}-f_{0}|}=1 ρ(Q)t∣fopt−f0∣∣fopt−ft∣=1
从推论显而易见可以看出其成指数衰减的趋势。下面实验验证这个结论。首先介绍实验算法和问题。
2.OneMax问题和(1+1)EA
2.1 OneMax问题
由于OneMax已被证明是最简单的适应度函数,其经常被使用到其他理论证明中。OneMax顾名思义就是一个给定的字符串 x = ( s 1 , s 2 , . . . , s n ) ∈ 0 , 1 n x=(s_1,s_2,...,s_n)\in{0,1}^n x=(s1,s2,...,sn)∈0,1n中1的个数,其函数的最优解就是一个全为1的串。我们将此问题的适应度分为n个等级,每个等级 f l f_l fl满足以下关系
S l = { x ∣ h ( x , 1 ⃗ = l ) } , f l = n − l , l = 0 , . . . , n S_l=\left\{ x|h(x,\vec{1}=l) \right\},f_l=n-l,l=0,...,n Sl={x∣h(x,1=l)},fl=n−l,l=0,...,n
这里的 h ( x , y ) h(x,y) h(x,y)是x和y之间的汉明距离。
2.2 (1+1)EA
为了简单分析,这里使用(1+1)EA,其步骤如下:
Input:编码长度,定义域,迭代次数,种群大小,适应度函数 f ( x ) f(x) f(x);
output:最优种群
begin
ϕ 0 : = \phi_0:= ϕ0:=随机初始化一个解;
for(k=0 to K-1)do
ϕ k ′ : = m u t a t i o n ( ϕ k ) \phi_{k}^{'}:=mutation(\phi_{k}) ϕk′:=mutation(ϕk):采用单点变异;
if f ( ϕ k ′ ) > f ( ϕ k ) f(\phi^{'}_k)>f(\phi_k) f(ϕk′)>f(ϕk) then
ϕ k + 1 : = ϕ k ′ \phi_{k+1}:=\phi^{'}_k ϕk+1:=ϕk′;
else
ϕ k + 1 : = ϕ k \phi_{k+1}:=\phi_k ϕk+1:=ϕk;
end if
end
输出结果。
end
2.3 实验
定义子集 S k : = { x : ∣ x ∣ = n − k } S_k:=\left\{x:|x|=n-k\right\} Sk:={x:∣x∣=n−k}这里 k = 0 , . . . , n k=0,...,n k=0,...,n, ∣ x ∣ |x| ∣x∣即为串中1的个数。转换概率满足 P r ( ϕ t + 1 ∈ S k − 1 ∣ ϕ t ∈ S k ) = k / n Pr(\phi_{t+1}\in S_{k-1}|\phi_t\in S_k)=k/n Pr(ϕt+1∈Sk−1∣ϕt∈Sk)=k/n并且 P r ( ϕ t + 1 ∈ S k ∣ ϕ t ∈ S k ) = 1 − k / n Pr(\phi_{t+1}\in S_{k}|\phi_t\in S_k)=1-k/n Pr(ϕt+1∈Sk∣ϕt∈Sk)=1−k/n。那么矩阵P为
( 1 0 0 . . . 0 0 0 1 / n 1 − 1 / n 0 . . . 0 0 0 0 2 / n 1 − 2 / n . . . 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 . . . ( n − 1 ) / n 1 − ( n − 1 ) / n 0 0 0 0 . . . 0 1 0 ) \left ( \begin{matrix} 1 & 0 & 0 & ... & 0 & 0 & 0 \\ 1/n & 1-1/n & 0 & ... & 0 & 0 & 0 \\ 0 & 2/n & 1-2/n & ... & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & ... & (n-1)/n & 1-(n-1)/n & 0 \\ 0 & 0 & 0 & ... & 0 & 1 & 0 \end{matrix}\right ) ⎝⎜⎜⎜⎜⎜⎜⎜⎛11/n0⋮0001−1/n2/n⋮00001−2/n⋮00.........⋮......000⋮(n−1)/n0000⋮1−(n−1)/n1000⋮00⎠⎟⎟⎟⎟⎟⎟⎟⎞
那么子矩阵Q为
( 1 − 1 / n 0 . . . 0 0 0 2 / n 1 − 2 / n . . . 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 . . . ( n − 1 ) / n 1 − ( n − 1 ) / n 0 0 0 . . . 0 1 0 ) \left ( \begin{matrix} 1-1/n & 0 & ... & 0 & 0 & 0 \\ 2/n & 1-2/n & ... & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & ... & (n-1)/n & 1-(n-1)/n & 0 \\ 0 & 0 & ... & 0 & 1 & 0 \end{matrix}\right ) ⎝⎜⎜⎜⎜⎜⎛1−1/n2/n⋮0001−2/n⋮00......⋮......00⋮(n−1)/n000⋮1−(n−1)/n100⋮00⎠⎟⎟⎟⎟⎟⎞
那么谱半径 ρ ( Q ) = 1 − 1 / n \rho(Q)=1-1/n ρ(Q)=1−1/n,渐进平均收敛率 R ∞ = 1 / n R_{\infty}=1/n R∞=1/n。易知, 1 / R ∞ = n 1/R_{\infty}=n 1/R∞=n不会超过最大的期望运行时间( = n ( 1 + 1 / 2 + . . . + 1 / n ) =n(1+1/2+...+1/n) =n(1+1/2+...+1/n))。
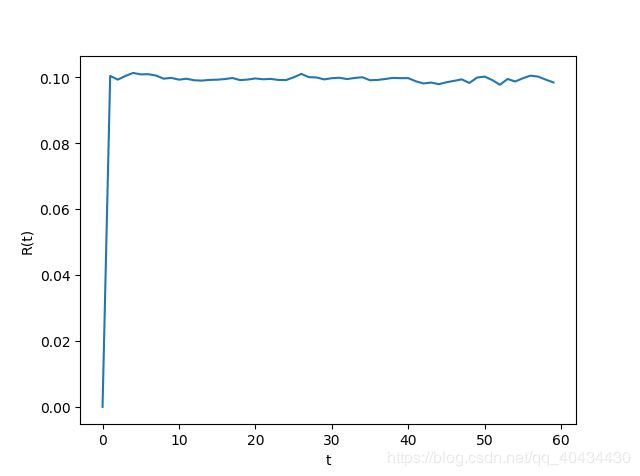
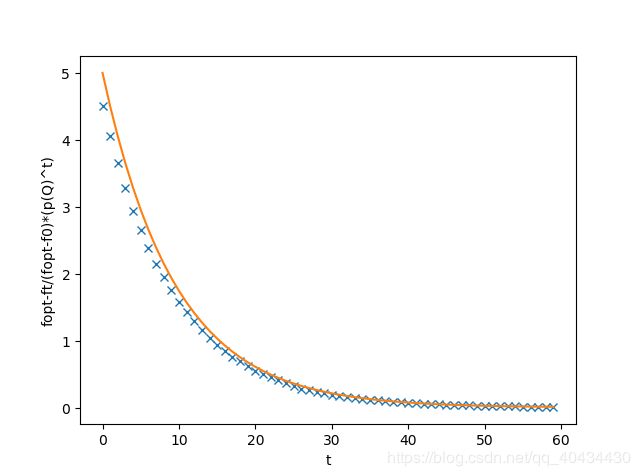
此次实验设置 n = 10 , ρ ( Q ) = 0.9 , R ∞ = 0.1 n=10,\rho(Q)=0.9,R_{\infty}=0.1 n=10,ρ(Q)=0.9,R∞=0.1。 ϕ 0 \phi _0 ϕ0均匀初始化,那么 f 0 ≈ 5 f_0\approx 5 f0≈5。运行(1+1)EA2000次,每次60代。计算R(t)如图3所示。计算 ∣ f o p t − f t ∣ |f_{opt}-f_{t}| ∣fopt−ft∣和 ρ ( Q ) t ∣ f o p t − f 0 ∣ \rho(Q)^t|f_{opt}-f_{0}| ρ(Q)t∣fopt−f0∣如图4所示。
由图3易知,R(t)大约为0.1。图4中"x"为 ∣ f o p t − f t ∣ |f_{opt}-f_{t}| ∣fopt−ft∣,"—"为 ρ ( Q ) t ∣ f o p t − f 0 ∣ \rho(Q)^t|f_{opt}-f_{0}| ρ(Q)t∣fopt−f0∣,其说明理论指数衰减的合理性,并且 ∣ f o p t − f t ∣ |f_{opt}-f_{t}| ∣fopt−ft∣和 ρ ( Q ) t ∣ f o p t − f 0 ∣ \rho(Q)^t|f_{opt}-f_{0}| ρ(Q)t∣fopt−f0∣的曲线几乎一致,从而验证了推论1。
2.4 python代码
(1+1)EA在OneMax问题上的python代码(python3.6):
import numpy as np
import matplotlib.pyplot as plt
#参数设置-----------------------------------------------------------------------
expnum = 2000#每次问题的实验次数
maxgen=60#最大迭代次数
popsize=1#种群大小
n=10#染色体长度
opt=''#最优解为全1
f0=5
pq=0.9
t0=10
#初始化种群
def init(popsize,n):
population=[]
for i in range(popsize):
pop=''
for j in range(n):
#pop=pop+str(np.random.randint(0,2))
if(j<n/2):
pop=pop+'1'
else:
pop=pop+'0'
population.append(pop)
return population
#适应度函数
def fitnessfun(populationn,n):
fun11=[]
for i in range(len(populationn)):
dd = 0
for j in range(n):
if(populationn[i][j] == '1'):
dd = dd + 1
fun11.append(dd)
return fun11,populationn
#单点变异
def mutation(offspring1):
offspring=offspring1.copy()
for i in range(len(offspring)):
point=np.random.randint(0,len(offspring[i]))
if offspring[i][point]=='1':
offspring[i]=offspring[i][:point]+'0'+offspring[i][(point+1):]
else:
offspring[i]=offspring[i][:point]+'1'+offspring[i][(point+1):]
return offspring
#主程序----------------------------------------------------------------------------------------------------------------------------------
for i in range(n):
opt=opt+'1'
ff=np.zeros([expnum,maxgen])#储存每次实验的适应度
for i in range(expnum):#2000次实验
print("第{name}次实验".format(name=i))
#初始化-------------------------------------------------------------------------
#初始化种群(编码)
population=init(popsize,n)
#适应度值计算(解码)
fun11,population = fitnessfun(population,n)
#初始化储存种群的最优值
maxre=max(fun11)
#循环---------------------------------------------------------------------------
j=0
while(j<maxgen):#maxre!=n and
#print("迭代次数:{name}".format(name=j+1))
#一点变异
offspring=mutation(population)
#适应度函数计算
LO1,population1 = fitnessfun(population,n)
LO2,population2 = fitnessfun(offspring,n)
#选择
for k in range(popsize):
if LO1[k]>=LO2[k]:
population[k]=population1[k]
else:
population[k]=population2[k]
fun11,population = fitnessfun(population,n)
#储存当代的最优解
maxre=max(fun11)
ff[i][j]=maxre
j=j+1
i=i+1
ft=np.mean(ff, axis=0)
RT=ft.copy()
fopdft=n-RT #fopt-ft
foptdf0=np.zeros(maxgen)
foptdf0=foptdf0+n-f0
for i in range(RT.shape[0]):
if i==0:
RT[0]=0
else:
if ft[0]==n:
RT[i] = 1
else:
RT[i]=1-(abs(n-ft[i])/abs(n-ft[0]))**(1/i)
foptdf0[i] = foptdf0[i]*(pq**i)
i = 0
Rtt=[]#横坐标
Rtxx=[]#纵坐标
while(i < maxgen):
Rtt.append(i)
if(i<t0 or i>maxgen-t0-1):
Rtxx.append(0)
else:
rxt=1-(abs((ft[i+t0]-ft[i])/(ft[i]-ft[i-t0])))**(1/t0)
Rtxx.append(rxt)
i = i+1
#画出收敛曲线
plt.figure(1)
plt.plot(RT)
#plt.title('R(t) for the (1+1)EA on the OneMax function',color='#123456')
plt.xlabel('t')
plt.ylabel('R(t)')
plt.show()
plt.figure(2)
plt.plot(fopdft,'x',foptdf0)
#plt.title('comparison of the theoretical prediction (fopt-f0)*(p(Q)^t) and the computational result fopt-ft',color='#123456')
plt.xlabel('t')
plt.ylabel('fopt-ft/(fopt-f0)*(p(Q)^t)')
plt.show()
plt.figure(3)
plt.plot(Rtt,Rtxx)
#plt.title('R*(t) for the (1+1)EA on the OneMax function',color='#123456')
plt.xlabel('t')
plt.ylabel('R*(t)')
plt.show()
VI 迭代速率
最后谈一下在最优解未知的情况下如何定义收敛速率。此处介绍一个交替平均收敛速率
R ′ ( t ) : = 1 − ( ∣ f t + τ − f t f t − f t − τ ∣ ) 1 / τ R^{'}(t):=1-(|\frac{f_{t+\tau}-f_t}{f_{t}-f_{t-\tau}}|)^{1/\tau} R′(t):=1−(∣ft−ft−τft+τ−ft∣)1/τ
这里 τ \tau τ是一个适当的时间间隔,它的取值依赖于EA和优化问题。
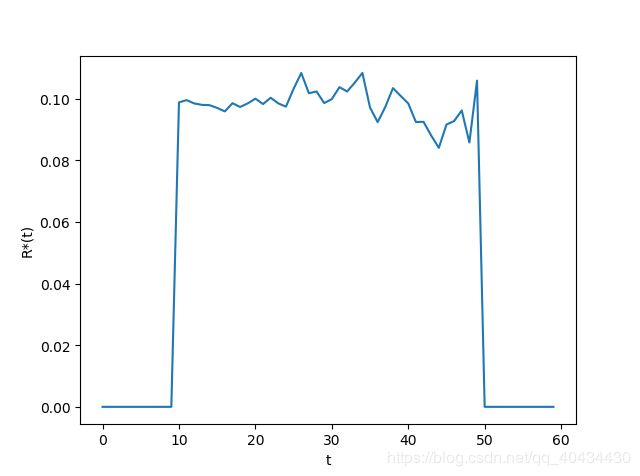
使用V中的(1+1)EA,OneMax问题以及实验设置,令 τ = 10 \tau=10 τ=10,根据(37)计算 R ′ ( t ) R^{'}(t) R′(t),得到结果如图5所示。
由图可知,t只在[10,50)的范围内有值(由于 τ = 10 \tau=10 τ=10)。 R ′ ( t ) R^{'}(t) R′(t)大约为0.1。其等于 1 − ρ ( Q ) 1-\rho(Q) 1−ρ(Q)。以下通过理论证明这个结果的合理性。
定理3:令Q为收敛EA的一个转换子矩阵。
1)在特定的初始化下(设置 q 0 = v / ∣ v ∣ q_0=v/ |v| q0=v/∣v∣,这里v是特征值 ρ ( Q ) \rho(Q) ρ(Q)相应的特征向量,这里 v ≥ 0 v\geq0 v≥0但 v ≠ 0 v\neq0 v̸=0),则对于所有的 t ≥ 1 t\geq1 t≥1
R ′ ( t ) = 1 − ρ ( Q ) R^{'}(t)=1-\rho(Q) R′(t)=1−ρ(Q)
2)在随机初始化下( q 0 > 0 q_0>0 q0>0),对于一个最大化问题(或者对于一个最小化问题 g < 0 g<0 g<0)选择一个适当的 τ \tau τ使得 g : = ( I − Q τ ) ( f o p t 1 − f ) > 0 g:=(I-Q^{\tau})(f_{opt}1-f)>0 g:=(I−Qτ)(fopt1−f)>0。如果Q是正的,则
l i m t → + ∞ R ′ ( t ) = 1 − ρ ( Q ) lim_{t\rightarrow+\infty}R^{'}(t)=1-\rho(Q) limt→+∞R′(t)=1−ρ(Q)
注:对于最大化问题,因为 l i m τ → + ∞ ( I − Q τ ) = I lim_{\tau\rightarrow+\infty}(I-Q^{\tau})=I limτ→+∞(I−Qτ)=I并且 f o p t 1 − f > 0 f_{opt}1-f>0 fopt1−f>0,那么选一个大的时间间隔就可以了。
证明:考虑 q t T = q t − 1 T Q q^T_t=q^T_{t-1}Q qtT=qt−1TQ以及 f o p t − f t = q t T ⋅ ( f o p t 1 − f ) f_{opt}-f_t=q_t^T\cdot(f_{opt}1-f) fopt−ft=qtT⋅(fopt1−f)得到
f t + τ − f t = f o p t − f t + f t + τ − f o p t = q t T ⋅ ( f o p t 1 − f ) − q t + τ T ⋅ ( f o p t 1 − f ) f_{t+\tau}-f_t=f_{opt}-f_t+f_{t+\tau}-f_{opt}=q_t^T\cdot(f_{opt}1-f)-q_{t+\tau}^T\cdot(f_{opt}1-f) ft+τ−ft=fopt−ft+ft+τ−fopt=qtT⋅(fopt1−f)−qt+τT⋅(fopt1−f)
= q t T ⋅ ( f o p t 1 − f ) − q t T Q τ ( f o p t 1 − f ) = q t T ⋅ g =q_t^T\cdot(f_{opt}1-f)-q_{t}^TQ^{\tau}(f_{opt}1-f)=q_t^T\cdot g =qtT⋅(fopt1−f)−qtTQτ(fopt1−f)=qtT⋅g。
1)因为 q 0 q_0 q0是特征值 ρ ( Q ) \rho(Q) ρ(Q)对应的特征向量,那么 ρ ( Q ) q 0 T = q 0 T Q \rho(Q)q_0^T=q_0^TQ ρ(Q)q0T=q0TQ。又因为 q t T = q t − 1 T Q q^T_t=q^T_{t-1}Q qtT=qt−1TQ, f t + τ − f t = q t T ⋅ g f_{t+\tau}-f_t=q_t^T\cdot g ft+τ−ft=qtT⋅g
则
∣ f t + τ − f t f t − f t − τ ∣ 1 / τ = ∣ q t T ⋅ g q t − τ T ⋅ g ∣ 1 / τ = ∣ q 0 T Q t g q 0 T Q t − τ g ∣ 1 / τ = ∣ ρ ( Q ) t ρ ( Q ) t − τ × q 0 T ⋅ g q 0 T ⋅ g ∣ 1 / τ = ρ ( Q ) |\frac{f_{t+\tau}-f_t}{f_{t}-f_{t-\tau}}|^{1/\tau}=|\frac{q_t^T\cdot g}{q_{t-\tau}^T\cdot g}|^{1/\tau}=|\frac{q_0^TQ^t g}{q_{0}^TQ^{t-\tau} g}|^{1/\tau}=|\frac{\rho(Q)^t}{\rho(Q)^{t-\tau}}\times \frac{q_0^T\cdot g}{q_0^T\cdot g}|^{1/\tau}=\rho(Q) ∣ft−ft−τft+τ−ft∣1/τ=∣qt−τT⋅gqtT⋅g∣1/τ=∣q0TQt−τgq0TQtg∣1/τ=∣ρ(Q)t−τρ(Q)t×q0T⋅gq0T⋅g∣1/τ=ρ(Q)
因此1)得证。
2)不失一般性,假设 g > 0 g>0 g>0。因为
f t + τ − f t f t − f t − τ = q t T ⋅ g q t − τ T ⋅ g = q t − τ T Q τ g q t − τ T ⋅ g \frac{f_{t+\tau}-f_t}{f_{t}-f_{t-\tau}}=\frac{q_t^T\cdot g}{q_{t-\tau}^T\cdot g}=\frac{q_{t-\tau}^TQ^{\tau} g}{q_{t-\tau}^T\cdot g} ft−ft−τft+τ−ft=qt−τT⋅gqtT⋅g=qt−τT⋅gqt−τTQτg
令
λ ‾ t = m i n i [ q t − τ T Q τ ] i [ q t − τ T ] i , λ ‾ t = m a x i [ q t − τ T Q τ ] i [ q t − τ T ] i \underline{\lambda}_t=min_i\frac{[q^T_{t-\tau}Q^{\tau}]_i}{[q^T_{t-\tau}]_i},\overline{\lambda}_t=max_i\frac{[q^T_{t-\tau}Q^{\tau}]_i}{[q^T_{t-\tau}]_i} λt=mini[qt−τT]i[qt−τTQτ]i,λt=maxi[qt−τT]i[qt−τTQτ]i
这里 [ v ] i [v]_i [v]i代表向量 v v v的第i项。
根据Collatz formula,得
l i m t → + ∞ λ ‾ t = l i m t → + ∞ λ ‾ t = ρ ( Q τ ) lim_{t\rightarrow+\infty}\underline{\lambda}_t=lim_{t\rightarrow+\infty}\overline{\lambda}_t=\rho(Q^{\tau}) limt→+∞λt=limt→+∞λt=ρ(Qτ)
这里对于任意的 [ g ] i > 0 [g]_i>0 [g]i>0,满足
l i m t → + ∞ m i n i [ q t − τ T Q τ ] i [ g ] i [ q t − τ T ] i [ g ] i = ρ ( Q τ ) lim_{t\rightarrow+\infty}min_i\frac{[q^T_{t-\tau}Q^{\tau}]_i[g]_i}{[q^T_{t-\tau}]_i[g]_i}=\rho(Q^{\tau}) limt→+∞mini[qt−τT]i[g]i[qt−τTQτ]i[g]i=ρ(Qτ)
l i m t → + ∞ m a x i [ q t − τ T Q τ ] i [ g ] i [ q t − τ T ] i [ g ] i = ρ ( Q τ ) lim_{t\rightarrow+\infty}max_i\frac{[q^T_{t-\tau}Q^{\tau}]_i[g]_i}{[q^T_{t-\tau}]_i[g]_i}=\rho(Q^{\tau}) limt→+∞maxi[qt−τT]i[g]i[qt−τTQτ]i[g]i=ρ(Qτ)
因为 m i n { a 1 / b 1 , a 2 / b 2 } ≤ ( a 1 + a 2 ) / ( b 1 + b 2 ) ≤ m a x { a 1 / b 1 , a 2 / b 2 } min\left\{ a_1/b_1,a_2/b_2 \right\}\leq(a_1+a_2)/(b_1+b_2)\leq max\left\{ a_1/b_1,a_2/b_2 \right\} min{a1/b1,a2/b2}≤(a1+a2)/(b1+b2)≤max{a1/b1,a2/b2},则
l i m t → + ∞ ∑ i [ q t − τ T Q τ ] i [ g ] i ∑ i [ q t − τ T ] i [ g ] i = ρ ( Q τ ) lim_{t\rightarrow+\infty}\frac{\sum_i[q^T_{t-\tau}Q^{\tau}]_i[g]_i}{\sum_i[q^T_{t-\tau}]_i[g]_i}=\rho(Q^{\tau}) limt→+∞∑i[qt−τT]i[g]i∑i[qt−τTQτ]i[g]i=ρ(Qτ)
相当于
l i m t → + ∞ q t − τ T Q τ g q t − τ T g = ρ ( Q τ ) lim_{t\rightarrow+\infty}\frac{q^T_{t-\tau}Q^{\tau}g}{q^T_{t-\tau}g}=\rho(Q^{\tau}) limt→+∞qt−τTgqt−τTQτg=ρ(Qτ)
那么
l i m t → + ∞ ∣ f t + τ − f t f t − f t − τ ∣ 1 / τ = ρ ( Q τ ) 1 / τ = ρ ( Q ) lim_{t\rightarrow+\infty}|\frac{f_{t+\tau}-f_t}{f_{t}-f_{t-\tau}}|^{1/\tau}=\rho(Q^{\tau})^{1/\tau}=\rho(Q) limt→+∞∣ft−ft−τft+τ−ft