粒子群算法（PSO）详解

1 粒子群PSO算法简介

1.1 维基百科的解释

粒子群算法（Particle Swarm Optimization，简称PSO），或称粒子群优化，是属于人工智能算法，公元1995年由肯尼迪（Kennedy）与埃伯哈特（Eberhart）（1995）两位学者所提出，这两位学者借由观察鸟类族群觅食的讯息传递所得到的一个启发，粒子群算法的理论基础是以单一粒子来做为鸟类族群之中的单一个体，于算法中赋予该粒子（个体）拥有记忆性，并能够透过与粒子群体中的其他粒子之间的互动而寻求到最适解。因此在粒子群算法的基础理论可以理解，任一个体（粒子）皆可用有自身移动过程中所产生的记忆与经验，当个体移动的同时，能依造自身的经验与记忆来学习调整自身的移动方向，由于在粒子群算法中，多个粒子是同时移动的，且同时以自身经验与其他粒子所提供的经验进行比对找寻最适当的解，并使自己处于最适解中，该粒子群算法的特性使得粒子不单单受自身演化的影响，同时会对群体间的演化拥有学习性、记忆性，并使粒子本身达到最佳调整。

1.2 三个简单的行为准则

①冲突避免：群体在一定空间移动，个体有自己的移动意志，但不能影响其他个体移动，避免碰撞和争执。
②速度匹配：个体必须配合中心移动速度，不管在方向、距离与速率都必须互相配合。
③群体中心：个体将会向群体中心移动，配合群体中心向目标前进。

1.3 基本理论公式

PSO是基于群鸟觅食而提出来的，是个最佳决策的过程，与人类决策的过程相似，往往基于两条重要的信息：他们的经验和自己的经验。
由此，在一个群鸟觅食中，在一个D维空间，有m个鸟组成群体，而第i个鸟的位置我们表示为

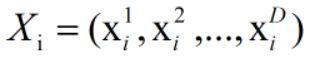
我们将这个位置代入目标函数便可以求出其的适应值，根据适应值的大小来确定该位置的好坏。假设我们记适应值越小该位置越好，则我们将每个鸟经历过的最好位置记为

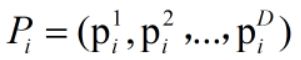
整个鸟群取的适应值最小的最好位置为

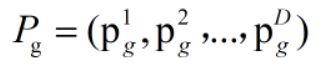
第i个鸟的速度记为

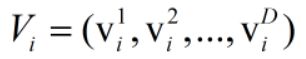
则粒子群算法便采用下面的公式使得粒子（鸟）的位置不断更新。

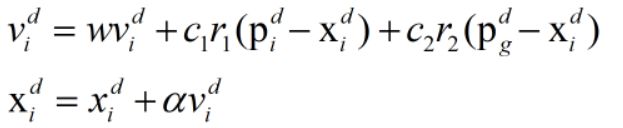
其中，i = 1,2,…,m，表示第 i 个粒子（鸟）；d = 1,2,…,D，表示第 d 维；w为非负数，称为惯性因子；r1和r2是[0,1]范围内变换的随机数；α称为约束因子，目的是控制速度的权重。

1.4 参数的选取

1.粒子数 m
一般取值为20~40，特殊难题需要100-200个粒子。粒子数量越多，搜索范围越大，越容易找到全局最优解，算法运行的时间也越长。

2.惯性常数 w
惯性因子w对于粒子群算法的收敛性有较大的影响。w可以取[0,1]区间的随机数，如果w是定值，建议取0.6~0.75区间的值。

3.加速常数c1和c2
加速常数c1和c2是调整自身经验和社会经验在其运动中所起作用的权重。一般情况下取c1 = c2 = 2；

4.最大飞翔速度
粒子最大飞翔速度一般不会超过最大速度的10%-20%。

2 算法流程

2.1 具体步骤

1.初始化粒子群（速度和位置）、惯性因子、加速常数、最大迭达次数和算法终止的最小误差。

2.评价每个粒子的初始适应值。

3.将初始适应值作为每个粒子的最优值，并将各适应值对应的位置作为每个粒子最优的位置。

4.将粒子中最好的适应值作为全局最好的最优值，并将各适应值对应的位置作为粒子全局最优的位置。

5.通过之前的公式更新粒子速度

6.对飞行速度进行限幅处理，使之不能超过最大飞翔速度

7.通过之前的公式更新粒子位置

8.比较每个粒子的适应值是否比历史的最优值好，如果是，则替换。

9.计算粒子全局最优的适应值是否比历史的最优值好，如果是，则替换。

10.重复5-9，直到满足设定的最小误差或者达到最大迭达次数。

11.输出最优粒子的全局最优值和其对应的位置以及每个粒子的局部最优值和对应的位置。

2.2 伪代码

For each particle
____Initialize particle
END
Do
____For each particle
________Calculate fitness value
________If the fitness value is better than the best fitness value (pBest) in history
____________set current value as the new pBest
____End
____Choose the particle with the best fitness value of all the particles as the gBest
____For each particle
________Calculate particle velocity according equation (a)
________Update particle position according equation (b)
____End
While maximum iterations or minimum error criteria is not attained

3 具体实现

建议采用MATLAB和Python，又相关的函数或库。

3.1 MATLAB

句法规则
x = particleswarm(fun,nvars)
x = particleswarm(fun,nvars,lb,ub)
x = particleswarm(fun,nvars,lb,ub,options)
x = particleswarm(problem)
[x,fval,exitflag,output] = particleswarm(___)

描述
x = particleswarm(fun,nvars)试图找到一个x达到局部最小值的向量fun。nvars是的尺寸（设计变量的数量）fun。
注意
传递额外参数（优化工具箱）介绍了如有必要，如何将额外参数传递给目标函数。

x = particleswarm(fun,nvars,lb,ub)定义了一组在设计变量下界和上界的，x，使得溶液中的范围内发现lb ≤ x ≤ ub。

x = particleswarm(fun,nvars,lb,ub,options)最小化，默认优化参数替换为中的值options。设置lb = []，ub = []如果没有界限。

x = particleswarm(problem)查找的最小值problem，其中problem为结构。

[x,fval,exitflag,output] = particleswarm(___)，对于上述任何输入参数，返回：
标量fval，是目标函数值fun(x)
一个exitflag描述退出条件的值
output包含有关优化过程信息的结构

3.2 Python

我们使用常用的 scikit-opt库，可在GitHub上进行下载。
具体例子如下
1.准备待优化的目标函数

def demo_func(x):
    x1, x2, x3 = x
    return x1 ** 2 + (x2 - 0.05) ** 2 + x3 ** 2

2.实施PSO算法，并打印结果

from sko.PSO import PSO
pso = PSO(func=demo_func, dim=3)
fitness = pso.fit()
print('best_x is ', pso.gbest_x, 'best_y is', pso.gbest_y)

4 扩展

一般我们可以使用粒子群算法和神经网络一起用，或者使用k-means聚类和粒子群算法一起用等等。具体相关研究以及参考可查看相关论文。