【数据库】第二章 关系数据库 笔记

一、关系的形式化定义和概念

1.1 域

域是一组具有相同数据类型的值的集合，又称为值域。 （用D表示）
域中所包含的值的个数称为域的基数（用m表示）。在关系中用域表示属性的取值范围。
如：D1={李力，王平，刘伟}，m=3； D2={男，女}；m=2； D3={18,20}；m=2

1.2 笛卡尔积

定义：给定一组域D1，D2，…，Dn（它们可以包含相同的元素，即可以完全不同，也可以部分或全部相同）。D1，D2，…，Dn的笛卡尔积为D1×D2×……×Dn={（d1，d2，…，dn）|di∈Di， i=1，2，…，n}
 每一个元素（d1，d2，…dn）中的每一个值di叫做一个分量（Component） ，di∈Di
 每一个元素（ d1，d2，…，dn）叫做一个n元组（n-Tuple），简称元组（Tuple）
笛卡尔积D1×D2×…×Dn的基数M（即元祖（d1，d2，…，dn）的个数）为所有域的基数的累乘之积。
如：
分量：李力、王平、刘伟、男、女
元组：（李力，男），（李力，女） ， M=m1×m2=3×2=6
笛卡尔积实际是一个二维表

1.3 关系

定义：笛卡尔积D1×D2×…×Dn的任一子集称为
定义在域D1，D2，…，Dn上的n元关系（Relation）

关系的相关概念：
 在关系R中，当n=1时，称为单元关系。当n=2时，称为二元关系，以此类推 。
 关系中的每个元素是关系中的元组，通常用t表示，关系中元组个数是关系的基数
 由于关系是笛卡尔积的子集，因此，也可以把关系看成一个二维表 。
 具有相同关系框架的关系称为同类关系。

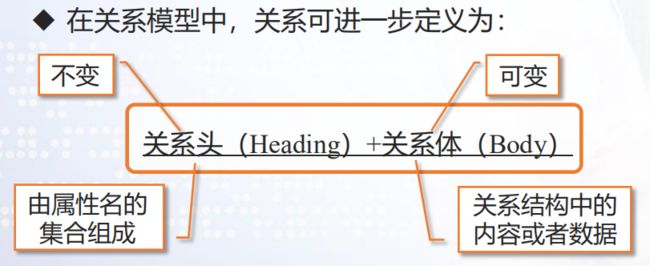
关系的性质：
一种规范化了的二维表中行的集合
 每一列中的分量必须来自同一个域，必须是同一类
型的数据。
 不同的列可来自同一个域，每一列称为属性，不同
的属性必须有不同的名字 。
 列的顺序可以任意交换，名字同时换。
 关系中元组的顺序（即行序）可任意。
 关系中每一分量必须是不可分的数据项

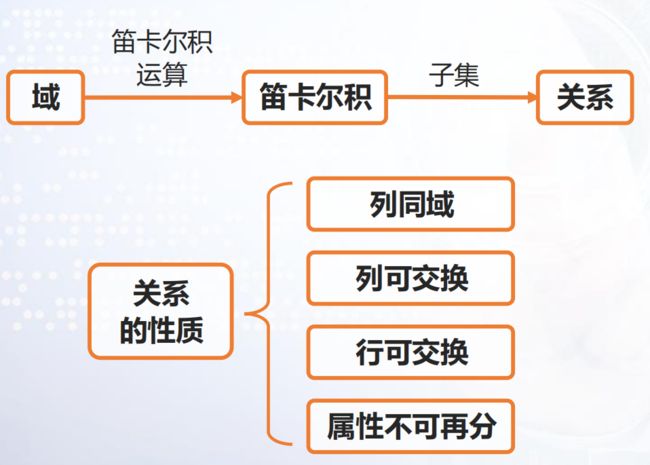
1.4 关系模式

关系的描述称为关系模式（RelationSchema） R–关系名
U–属性名集合
D–属性所来自的域
DOM–属性向域的映像集合
F–属性间数据的依赖关系集合
简记为：R（U）或R（ A1 ， A2，…，An），其中An为属性名
关系模式与关系的比较：

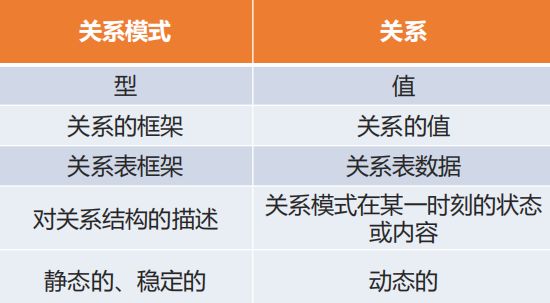
如，在在教学数据库中，包括关系模式可分别表示为：
学生（学号，姓名，性别，年龄，系别）
教师（教师号，姓名，性别，年龄，职称，
工资，岗位津贴，系别）
课程（课程号，课程名，课时）
选课（学号，课程号，成绩）
授课（教师号，课程号）

1.5 关系数据库与关系数据库模式

在给定领域中，所有实体以及实体之间的联系所对应的关系集合构成一个关系数据库。

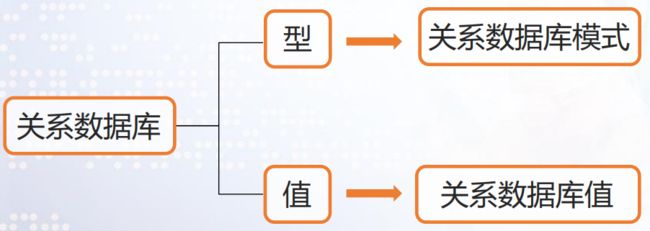
关系数据库模式
 对关系数据库的描述，由若干域的定义以及在这些域上定义的若干关系模式构成。
 描述了关系数据库的结构
 描述了关系数据库的框架。
关系数据库
 关系数据库在某一状态下对应的关系集合。
 描述了关系模式的内容。
 也称关系数据库实例。
小结：

二、关系的候选码、主码、外码

候选码
候选码（Candidate Key）
定义：能惟一标识关系中元组的一个属性或属性集，称为候选码(Candidate Key)
性质：唯一性、最小性
如：“学生关系”中的学号能惟一标识每一个学生； “选课关系”中，只有属性的组合“学号+课程号”才能惟一地区分每一条选课记录
主码
定义：从多个候选键中选择一个作为查询、插入或删除元组的操作变量，被选用的候选码称为主关系码（主键，主码，关系键，关键字）
每个关系必定有且仅有一个主码，选定后不能重复
 主属性（Prime Attribute）： 包含在主码中的各个属性称为主属性
 非主属性（Non-Prime Attribute）：不包含在任何候选码中的属性称为非主属性（或非码属性）
 全码 ：所有属性的组合是关系的候选码
 超码：包含候选码的属性集合。

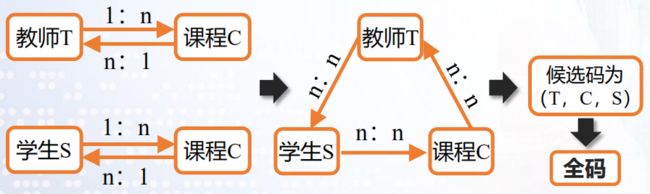
外码
定义：如果关系R2的一个或一组属性X不是R2的主码，而是另一个关系R1的主码，则该属性或属性组X称为关系R2的外部关键键或外码(Foreign Key)，并称R2为参照关(ReferencingRelation)，关系R1称为被参照关系(Referenced Relation)
被参照关系的主码和参照关系的外码必须定义在同一个域上

小结：

三、关系的完整性

关系的完整性概述
为了维护关系数据库中数据与现实世界的一致性，对关系数据库的插入、删除和修改操作必须有一定的约束条件，这些约束条件实际上是现实世界的要求。任何关系在任何时刻都要满足这些语义约束。
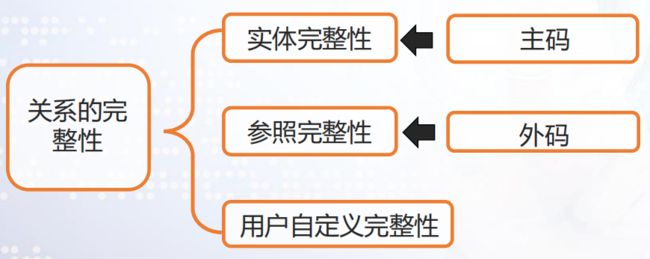
三类完整性约束
01 实体完整性 必须满足的性质
02 参照完整性 必须满足的性质
03 用户自定义完整性 具体领域的语义约束

实体完整性
实体完整性是指主码的值不能为空或部分为空。
参照完整性
如果关系R2的外码X与关系R1的主码相符， 则X的每个值或者等于R1中主码的某一个值或者取空值。
用户自定义完整性
用户自定义完整性是针对某一具体关系数据库的约束条件，它反映某一具体应用所涉及的数据必须满足的语义要求。
关系模型应该提供定义和检验这类完整性的机制，以便用统一的、系统的方法处理它们，而不要由应用程序承担这一功能。
小结：

四、关系代数

 关系代数是一种抽象的查询语言
 关系代数的运算对象与运算结果都是关系
 关系代数运算符

关系代数的运算按运算符的不同主要分为两类：传统的集合运算、专门的关系运算
传统的集合运算：把关系看成元组的集合，以元组作为集合中元素来进行运算，其运算是从关系的“水平”方向即行的角度进行的。包括并、差、交和广义笛卡尔积等运算。
专门的关系运算：不仅涉及行运算，也涉及列运算，这种运算是为数据库的应用而引进的特殊运算。包括选取、投影、连接和除法等运算。

传统的集合运算
传统集合（除笛卡尔积）是典型的二目运算，因此，需要在两个关系中进行，两个关系R、S，若满足：（１） 具有相同的度n; （２） R中第i个属性和S中第i个属性必须来自同一个域。（列同质）则说关系R、S是相容的
并（Union） R∪S={t | t∈R∨t∈S}
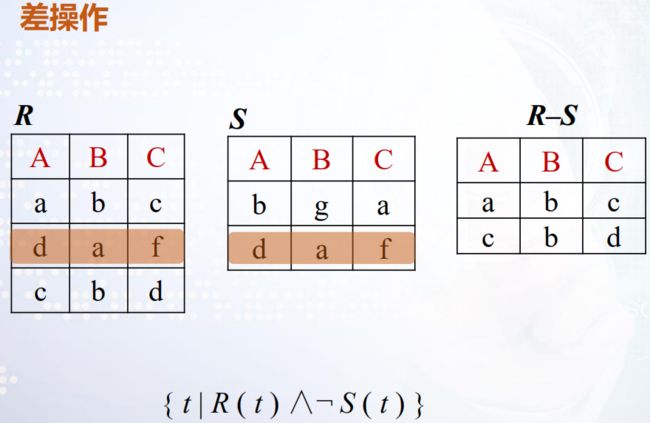
差（Difference） R-S = {t | t∈R∧┐t∈S}
交（Intersection） R∩S = {t | t∈R∧t∈S}
广义笛卡尔积（Extended Cartesian Product） R×S = {tr⌒ts| tr∈R∧ts∈S}
应用：并运算：在学生表增加一条记录
应用：差运算：在学生表删除一条记录

专门的关系运算符
（1）设关系模式为R(A1,A2,……An)，它的一个关系为R，t∈R表示t是R的一个元组，t[Ai]则表示元组t中相应于属性Ai的一个分量。
（2）若A={Ai1,Ai2,……，Aik}，其中Ai1,Ai2,……,Aik是A1,A2,……，An中的一部分，则A称为属性列或域列，Ã则表示{A1,A2,……， An}中去掉{Ai1,Ai2,……，Aik}后剩余的属性组。t[A]{t[Ai1],t[Ai2],……,t[Aik]}表示元组t在属性列A上诸分量的集合。
（3）R为n目关系，S为m目关系，tr∈R, ts∈S,tr ⌒ ts称为元组的连接(concatenation)，它是一个n+m列的元组，前n个分量为R的一个n元组，后m个分量为S中的一个m元组。
（4）给定一个关系R（X，Z），X和Z为属性组，定义当t[X]=x时，x在R中的象集(image set)，为Zx={t[Z]|t∈R,t[X]=x},它表示R中的属性组X上值为x的诸元组在Z上分量的集合。
选取（Selection）

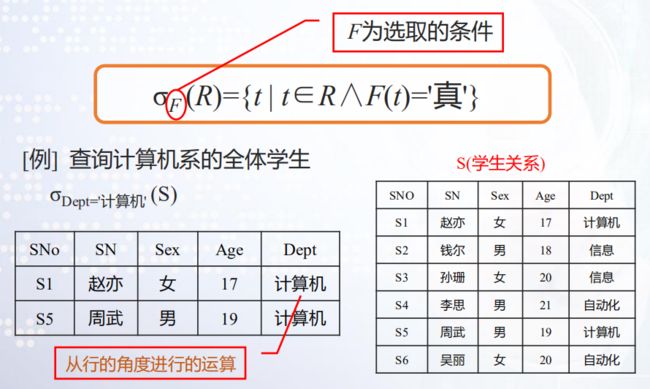
投影（Projection）

五、链接、自然链接和除法

Θ连接
设两个关系R和S，其中R中的属性可以进一步分解为属性集Z和X，即R=（Z，X）。关系S可以进一步分解为属性集W和Y，即S=（W，Y）。
 关系R和S在连接属性X和Y上Θ连接，就是在R和S的笛卡儿积中，选取X属性上的分量与Y属性列上的分量满足比较条件的那些元组。R ⋈XθYS= tr⌒ts tr∈R ⋀ ts∈S ⋀ tr X θts Y 为真}
Θ连接是二目运算符，是从两个关系的笛卡儿积中选择满足条件的元组，组成新的关系。
Θ连接的运算符==：==

自然连接
在等值连接的情况下，当连接属性X与Y具有相同属性组时，把在连接结果中重复的属性列去掉，
即如果R和S具有相同的属性组Y，则自然连接可以记作：R⋈S= tr⌒ts tr∈R ⋀ ts∈S ⋀ tr [Y] =ts[ Y]}
Θ连接与自然连接例子：

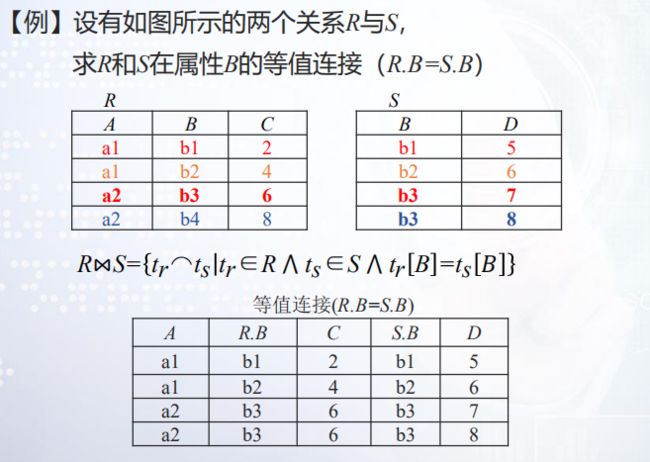
Θ连接和自然连接区别及实际例子：

除法
除法运算是二目运算，设有关系R（X，Y）与关系S（Y，Z），其中X，Y，Z为属性集合，R中的Y与S中的Y可以有不同的属性名，但对应属性必须出自相同的域。
关系R除以关系S所得的商是一个新关系P（X），P是R中满足下列条件的元组在X上的投影：元组在X上分量值x的像集Yx包含S在Y上投影的集合：
R÷S = {tr[X ] | tr∈R∧Πy(S)Yx} 其中，Yx为x在R中的像集，x =tr[X]
例子：

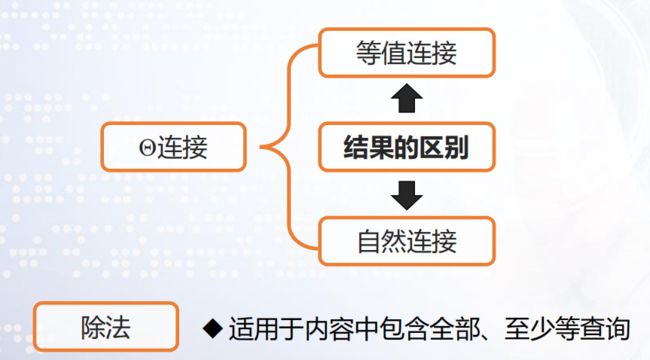
除法运算同时从行和列的角度进行运算，适合于包含“全部”和“至少”之类的短语的查询

小结：

六、元组关系演算

定义
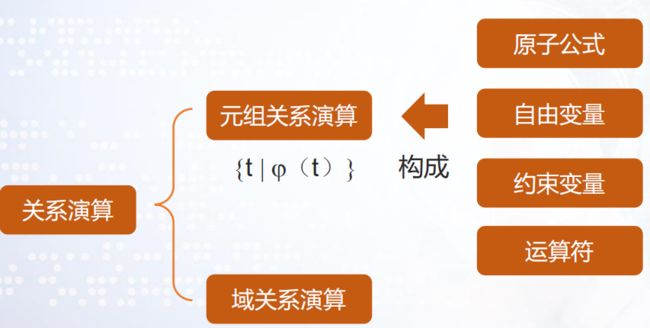
元组关系演算中，以元组为单位，通过谓词公式约束所要查找元组的条件，可以表示为：

元组关系演算与关系代数的关系

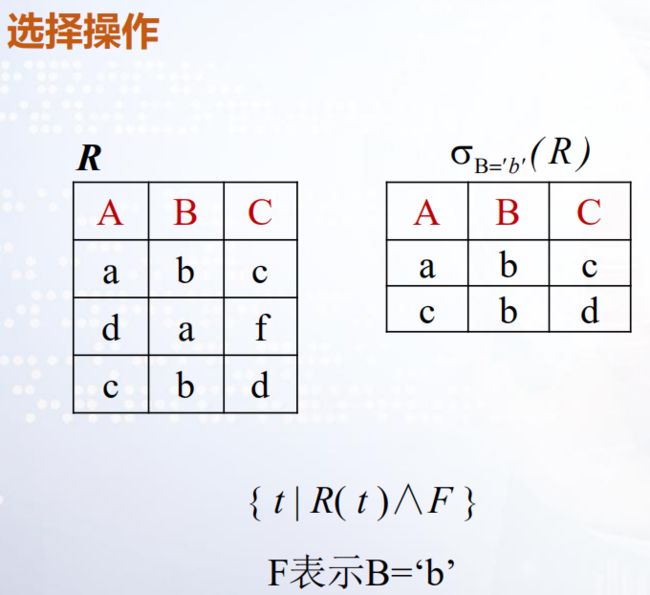
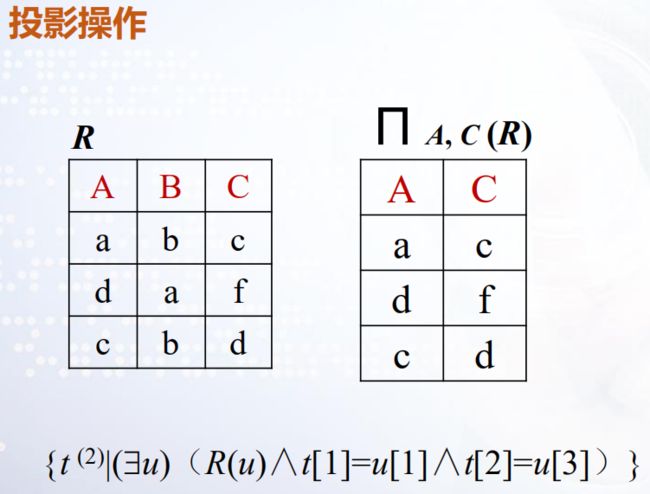
例子

使用元组关系演算实现查询的注意事项：
语句形式化过程需要注意如下问题
 准确地从查询语句中提取谓词，即元组变量和元组分量所满足的谓词条件。
 涉及某个关系上的全部个体或某个个体时，使用限于该关系的“限定谓词”。
 准确确定量词和量词的辖域，当辖域中多于一个谓词时必须注意括号的使用
小结

七、域关系演算

定义
定义 以元组中的域为单位，按照谓词公式所约束的条件查询所需的元组，表示为：{ | R(x1, x2, …, xn) }其中x1, x2, …, xn代表域变量，即元组的分量，R代表由原子构成的公式。
R的定义如元组关系演算，同样是反复由原子公式、自由变量、约束变量和运算符构成。
域关系演算语言
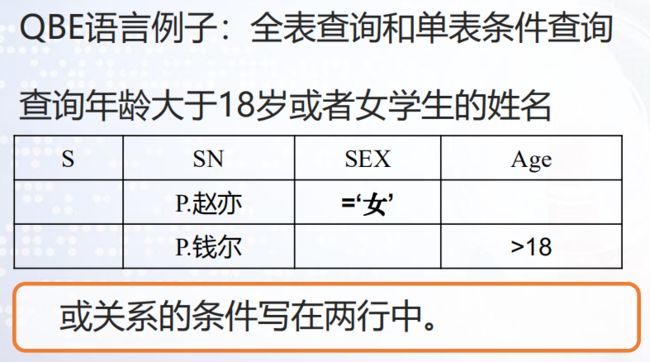
域关系演算语言 QBE（Query By Example）是一种高度的非过程化，基于屏幕 表格的查询语言。用户通过填写表格，并给出查询事例的方式获取结果。给出的查询事例是域变量。

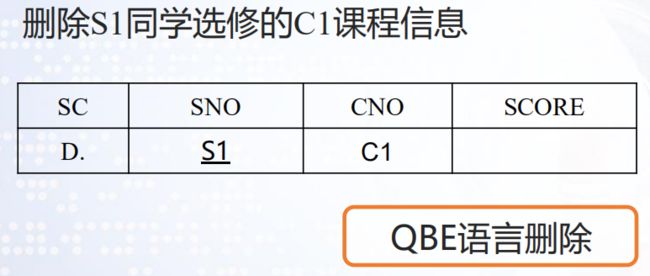
小结