解决最长回文子串问题——Manacher算法
问题描述:
输入一个字符串,求出其中最大的回文子串。子串的含义是:在原串中连续出现的字符串片段。回文的含义是:正着遍历和倒着遍历得到的序列相同,如madam,lol,oppo,zz。
计算字符串的最长回文字串最简单的算法就是枚举该字符串的每一个子串,并且判断这个子串是否为回文串,这个算法的时间复杂度为O(n^3)的,而稍微优化的一个算法是枚举回文串的中点,这里要分为两种情况,一种是回文串长度是奇数的情况,另一种是回文串长度是偶数的情况,枚举中点再判断是否是回文串,这样能把算法的时间复杂度降为O(n^2),但数据大的话,依然让人无法满意,这时Manacher(谐音马拉车)算法横空出世,在线性时间复杂度内求出一个字符串的最长回文字串,达到了理论上的下界。但同时,此算法的应用也十分狭窄,只能解决此类问题。
算法要点前导:刚才在朴素的O(n^2)蛮力方法中要考虑串的长度问题为奇数还是偶数,但马拉车算法使用了一个巧妙的方法解决了这个问题,在原序列中加上分隔符,使序列原本无论奇偶都变了奇数长度[i + (i+1)一定为奇数]。
比如oppovivo这个串,我们在每两个字符之间加上一个特殊符号(通常为串中不曾出现的符号),通常用#来充当,这样变为了#o#p#p#o#v#i#v#o#,原本8个元素现在变为17个。
此处许多博主使用了一个优化方法:可在在首尾加上两个不同的特殊字符,这样可以省去边界的判断,希望大家感兴趣自行添加。
『此处代码块』
//s_new为修改后的字符串
void init(string s){
string s_new;
int len = s.length();
s_new.resize(2*len+5);
s_new[0] = '#';
for(int i = 1; i <= len; i++){
s_new[2*i-1] = s[i-1];
s_new[2*i] = '#';
}
s_new[2*len] = '#';
}『Manacher算法原理及实现过程』
1.Len数组的意义及性质
Manacher算法用一个辅助数组Len[i]表示以字符s_new[i]为中心的最长回文字串的最右字符到s_new[i]的长度(可以看成是回文子串的半径,最右边到中心点的距离),假设最右的元素下标为r,那么Len[i]=r-i+1。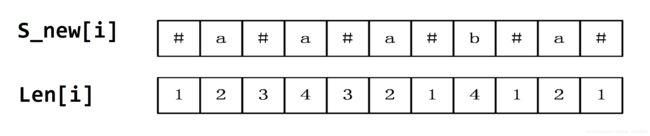
Len数组有一个性质,那就是Len[i]-1就是该回文子串在原字符串s中的长度。
证明:首先在转换得到的字符串str中,所有的回文字串的长度都为奇数,那么对于以s_new[i]为中心的最长回文字串,其长度就为2*Len[i]-1,经过观察可知,s_new中所有的回文子串,其中分隔符的数量一定比其他字符的数量多1,也就是有Len[i]个分隔符,剩下Len[i]-1个字符来自原字符串,所以该回文串在原字符串中的长度就为Len[i]-1。
有了这个性质之后,那么那么最长回文串问题就转化为求所有的Len[i]的最大值问题。
2.Len数组的计算
从1中我们已经明白Len数组的意义,那么求Len的方法也很简单,看关于中点i对称的两个元素是否对称,如果对称那么Len[i]++,如果不对称,则直接i++计算下一个点的长度Len[i+1]。但如果采用这种朴素算法,很显然会有很多的重复计算使得算法变得十分臃肿,这也恰恰体现了manacher的精髓:充分利用求解的答案,使复杂度降为O(n)。
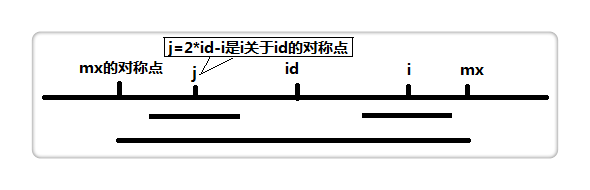
首先对变量给出解释:id为已经确定的一个最长回文子串的中点, i 和 j 为两个关于id对称的最长回文子串的中点,mx为id回文串的最右端点。
下面对具体的情况进行分类讨论:
Ⅰ.i > mx
这时前面的求解的信息没有办法利用,只能通过枚举的朴素算法来进行求解。
Ⅱ.i <= mx
可以利用前面已经得到的信息进行快速求解,主要使用Len[j]来加速查找。
(1):j 的回文串有一部分在 id 的回文串之外,i+Len[j] > mx,如下图:
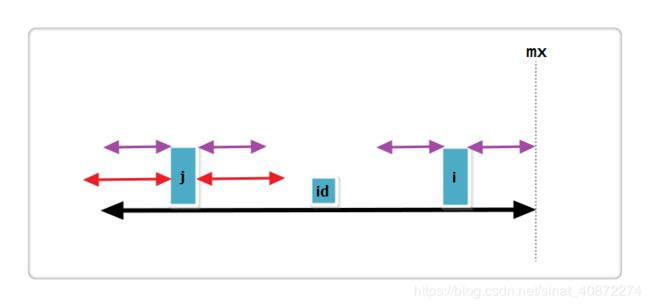
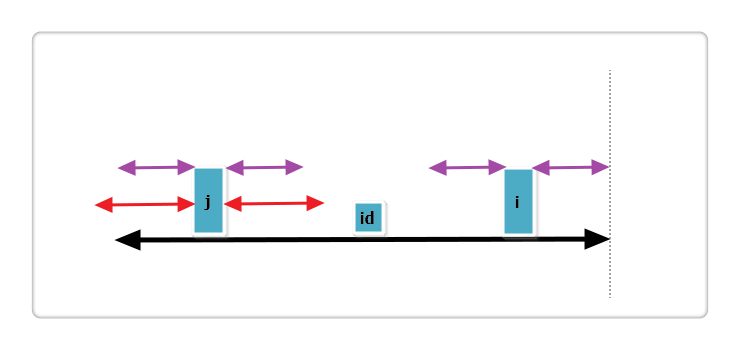
上图中,黑线为 id 的回文,i 与 j 关于 id 对称,红线为 j 的回文。那么此时Len[i] = mx - i,即紫线。那么Len[i]还可以更大么?答案是不可能!使用反证法可以得到结论,见下图:
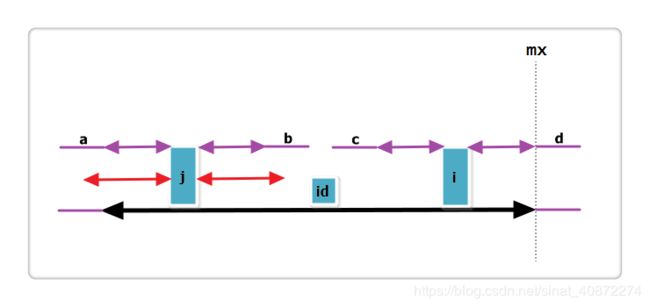
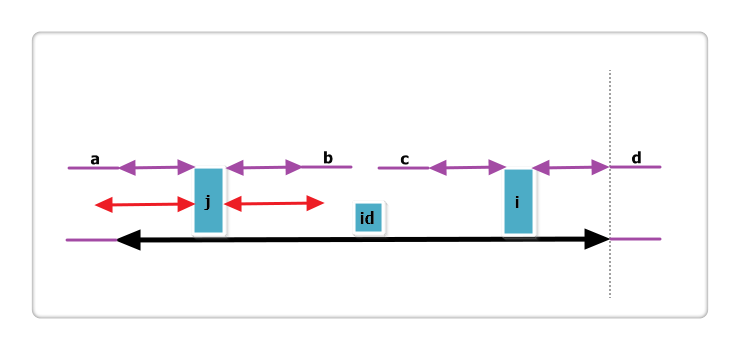
假设右侧新增的紫色部分是Len[i]可以增加的部分,那么根据回文的性质,a 等于 d ,也就是说 id 的回文不仅仅是黑线,而是黑线+两条紫线,矛盾,所以假设不成立,故Len[i] = mx - i,不可以再增加一分。
(2):j 回文串全部在 id 的内部,i+Len[j] < mx.如下图: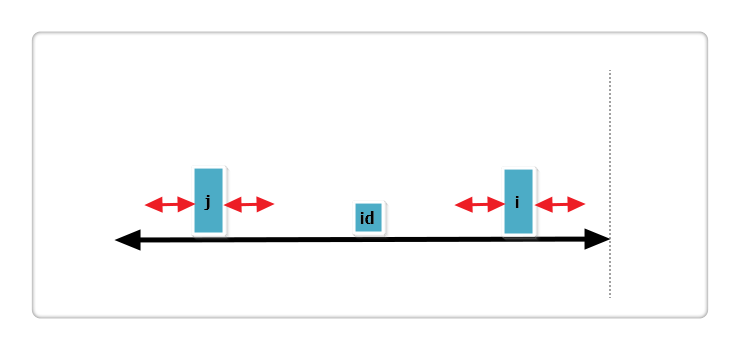
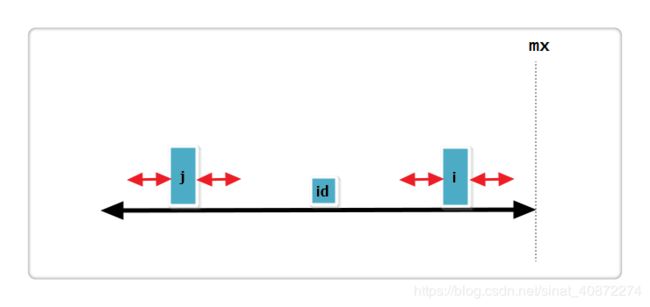
根据代码,此时Len[i] = Len[j],那么Len[i]还可以更大么?答案亦是不可能!见下图:
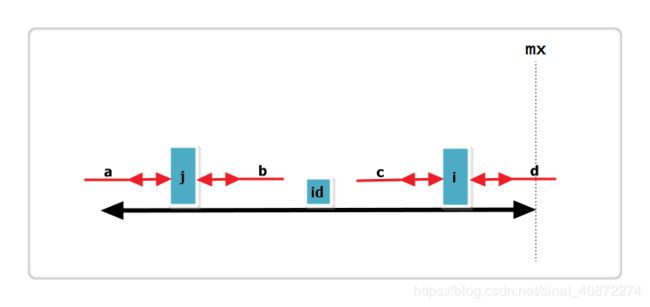
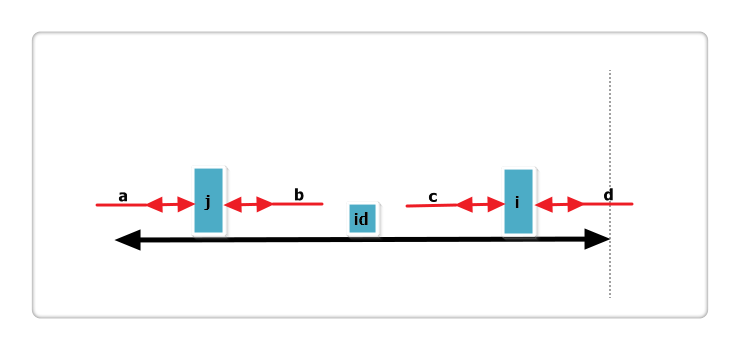
假设右侧新增的红色部分是Len[i]可以增加的部分,那么根据回文的性质,a 等于 b ,也就是说 j 的回文应该再加上 a 和 b ,矛盾,所以假设不成立,故Len[i] = Len[j],也不可以再增加一分。
(3):j 回文串左端正好与 id 的回文串左端重合,i+Len[j] = mx见下图:
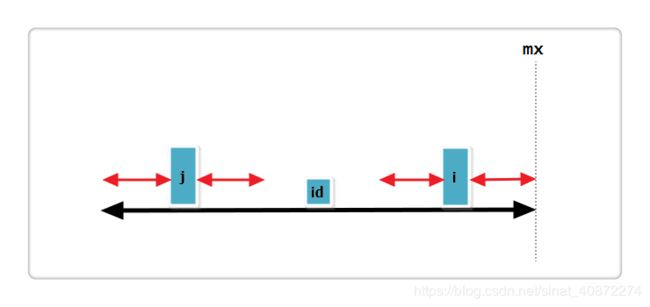
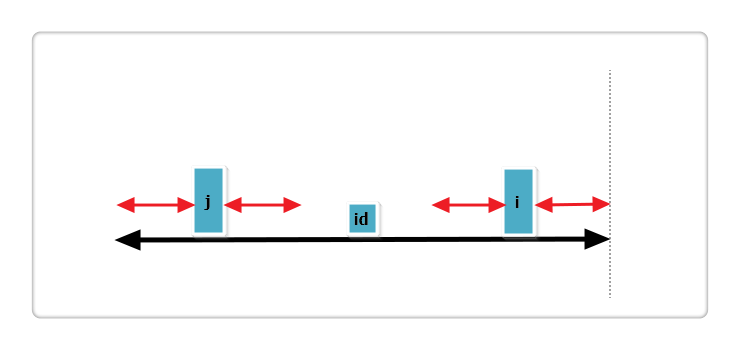
此时Len[i] = Len[j]或Len[i] = mx - i,并且Len[i]还可以继续增加,所以需要
while (s_new[i - Len[i]] == s_new[i + Len[i]])
Len[i]++;『初始版本代码』
#include
#include
#include
#include
using namespace std;
int n,len,len_new;
string s,s_new;
int Len[10000] = {0};
void init(string s) {
s_new.resize(2*len+5);
s_new[0] = '#';
for(int i = 1; i <= len; i++) {
s_new[2*i-1] = s[i-1];
s_new[2*i] = '#';
}
s_new[2*len] = '#';
}
int manacher() {
int ans = -1;
int id=0,mx=0;
Len[0] = 1;
Len[len_new-1] = 1;
for(int i = 1; i < len_new-1; i++) {
int j = 2*id-i;
if(i < mx && i + Len[j] < mx) {
Len[i] = Len[j];
continue;
} else if(i < mx && i + Len[j] >= mx ) {
if(i + Len[j] > mx)
continue;
Len[i] = mx-i;
} else {
Len[i] = 1;
}
while(s_new[i - Len[i]] == s_new[i + Len[i]])
Len[i]++;
if(Len[i] + i > mx) {
mx = Len[i]+i;
id = i;
}
}
for(int i = 0; i < len_new; i++)
ans = max(ans,Len[i]-1);
return ans;
}
int main() {
cin>>s;
len = s.length();
init(s);
len_new = 2*len+1;
cout<<"s_new = "<
『优化后代码』
//Manacher
#include
#include
#include
using namespace std;
const int MAXN = 1e5;
char str[MAXN];
char tmp[2*MAXN];
int len[2*MAXN];
int Manacher(char str[]) {
tmp[0] = '$';
tmp[1] = '#';
\ int str_len = strlen(str);
for(int i = 1; i <= str_len; i++) {
tmp[2*i] = str[i-1];
tmp[2*i+1] = '#';
}
tmp[2*str_len+2] = '\0';
//cout << tmp << endl;
int mx = 0;
int maxlen = -1;
int mid;
for(int i = 1; tmp[i]; i++) {
if(i < mx) len[i] = min(len[2*mid-i],mx-i);
else len[i] = 1;
while(tmp[i-len[i]] == tmp[i+len[i]]) len[i]++;
if(len[i]+i > mx) {
mx = len[i]+i;
mid = i;
}
maxlen = max(maxlen,len[i]-1);
}
return maxlen;
}
int main() {
//freopen("1.in","r",stdin);
scanf("%s",str);
cout << Manacher(str);
return 0;
}
图片和证明源自博客:https://segmentfault.com/a/1190000008484167?utm_source=tag-newest