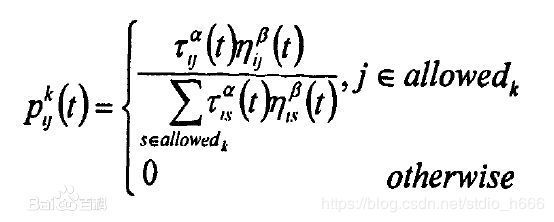智能优化算法之蚁群算法(1)

蚁群算法（ant colony algorithm） ： 一种模拟进化算法

蚂蚁在觅食过程中能够在其经过的路径留下一种称为信息素的物质，并在觅食的过程中能感知这种物质的强度，并指导自己的行动方向，他们总是朝着该物质强度高的方向移动，因此大量蚂蚁组成的集体觅食就表现为一种对信息素的正反馈现象。（非常符合常识对吧，这就是智能优化算法的魅力）
蚁群算法寻优的快速性是通过正反馈式的信息传递和积累来保证的。而算法的早熟性收敛又可以通过其分布计算特征加以避免。

下面介绍五种蚁群算法的过程：（第一种较经典，后四种均为改进方法）

1. 蚂蚁系统

    ①初始化 ： 初始时刻，m只蚂蚁随机放置，（第一次迭代）各条路径上的信息素初始值相等，设τij(t) = τ0为信息素初始值，可设τ0 = m/Lm，Lm是由最近邻启发式方法构造的路径长度。
    ②状态转移 ： 蚂蚁k(k = 1,2,...m)按照随机比例规则选择下一步要转移的城市，选择概率为
   

τij(t) 为边(i,j)上的信息素；
ŋij(t)是启发函数，表示蚂蚁从i到j的期望程度，其表达式为ŋij(t) = 1/dij,(dij为i到j的距离)；
allowedk为蚂蚁k下一步被允许访问的点集合；
α为信息启发因子，反应蚂蚁在运动过程中所积累的信息素在指导蚁群搜索中的相对重要程度；
β为期望启发因子，反应启发式信息在指导蚁群搜索过程中的相对重要程度。

③禁忌表 ： 为了不让蚂蚁选择已经访问过的地方，采用禁忌表的形式来记录蚂蚁k当前所走过的地方。
④信息素更新 ： 信息素挥发+信息素释放
信息素更新公式如下

其中ρ为信息素挥发因子，且ρ∈（0，1），ρ的大小直接影响到蚁群的全局搜索能力及收敛速度。
ρ过小时，以前搜索过的路径再次被选择的可能性变大，容易出现局部收敛现象。
ρ过大时，算法有较强的随机性和全局搜索能力，但搜索能力降低。

根据信息素更新策略的不同，Dorigo（蚁群算法的提出者）曾给出三种不同的模型，分别称为Ant-Cycle模型、Ant-Quantity模型和Ant-Density模型其区别在于Δ τijk(t)的计
算方式不同。其中Ant-Cycle模型利用的是整体信息，及蚂蚁完成一个循环（每个蚂蚁都走过了所有地方）后更新所有路径上的信息素（全局更新）；
Ant-Quantity模型和Ant-Density模型则利用的是局部信息，即蚂蚁完成一步后更新路径上的信息素（局部更新）。

Ant-Cycle	Δ τijk(t) = Q/Lk (Lk是第k只蚂蚁的路径长度)
Ant-Quantity	Δ τijk(t) = Q/dij（dij是i到j的距离）
Ant-Density	Δ τijk(t) = Q（Q为信息素强度）

Q为自定义数值，其作用是充分利用全局信息反馈量，使算法在正反馈机制的作用下以合理的速度找到问题最优解。Q越大，越有利于算法的快速收敛，但当Q特别大时，虽然收敛速度很快，但其全局搜索能力变差，易限于局部最优解，故其计算性能也不稳定。

（摘自 任瑞春.基于排序加权的蚁群算法[D].大连：大连海事大学，2006：16-17.）
我们上一章提过，智能优化算法具有随机性，参数选择依赖经验，就应用最多的Ant-Cycle模型而言，最好的经验结果是0≤α≤5；0≤β≤5；0.10≤ρ≤0.99；10≤Q≤10000（段海滨.蚁群算法原理及其应用[M].北京：科学出版社，2005）

⑤蚂蚁完成一次循环后，清空禁忌表，重新回到初始地点，准备下一次周游（循环）。

为了理解，附上解决相关问题的代码

%%TSP旅行商问题%%
%%算法：蚁群算法（蚂蚁系统+蚁周模型）%%

%%算法介绍：
%%①初始化 ：初始化 ： 初始时刻，m只蚂蚁随机放置。
%%②状态转移 ： 蚂蚁k(k = 1,2,...m)按照随机比例规则选择下一步要转移的城市。
%%③禁忌表 ： 为了不让蚂蚁选择已经访问过的地方，采用禁忌表的形式来记录蚂蚁k当前所走过的地方。
%%④信息素更新 ： 信息素挥发+信息素释放
%%⑤蚂蚁完成一次循环后，清空禁忌表，重新回到初始地点，准备下一次周游（循环）。

clear all;%清除工作区所有变量
%%常量设置（常量开头字母大写）
AntNum = 50;%%蚂蚁数量
Alpha = 3;%%信息启发因此α∈[0,5]   
Beta = 3;%%期望启发因子β∈[0,5]
Rho = 0.2;%%信息素挥发因子ρ∈[0.1,0.99]
Q = 1;%%蚁周模型信息素更新公式中参数Q∈[10,10000]
IterationTimes = 300;%%迭代（iteration）次数

%%城市的（x，y）坐标
Cities = [ 
    41 94;
    37 84;
    54 67;
    25 62;
    7 64;
    2 99;
    68 58;
    71 44;
    54 62;
    83 69;
    64 60;
    18 54;
    22 60;
    83 46;
    91 38;
    25 38;
    24 42;
    58 69;
    71 71;
    74 78;
    87 76;
    18 40;
    13 40;
    82 7;
    62 32;
    58 35;
    45 21;
    41 26;
    44 35;
    4 50
    ];
%%相关数据准备
CityNum = size(Cities,1);
DisMatrix = zeros(CityNum,CityNum);

bestRoute = zeros(IterationTimes,CityNum);%记录每次迭代最佳路线（其中包含全局最优解），用于蚁周模型更新信息素
bestDistance =inf.*ones(IterationTimes,1);%记录每次迭代最佳路线距离，用于求全局最优解，然后带入蚁周模型信息素更新模式中的Lk 
for i = 1:CityNum
    for j = i:CityNum %%矩阵为对称矩阵，故j可以从i开始，然后令disMatrix（j，i） = disMatrix（i，j）即可
        if i~=j
            DisMatrix(i,j) = ((Cities(i,1)-Cities(j,1))^2+(Cities(i,2)-Cities(j,2))^2)^(1/2);
        else
            DisMatrix(i,j) = eps;
        end
        DisMatrix(j,i) = DisMatrix(i,j);
    end
end

EtaMatrix = 1./DisMatrix;%%ηij（t）启发函数
PheromoneMatrix = ones(CityNum,CityNum);%%信息素（pheromone）矩阵（Matrix）
Tabu = zeros(AntNum,CityNum);%%禁忌表（tabu table）

%%迭代开始
for count = 1:IterationTimes
    %%①初始化 ：初始化 ： 初始时刻，m只蚂蚁随机放置。
    for i = 1:AntNum
        Tabu(i,1) = ceil(rand*CityNum);
    end
    %%②状态转移 ： 蚂蚁k(k = 1,2,...m)按照随机比例规则选择下一步要转移的城市。
    for i = 2:CityNum
        for j = 1:AntNum
            visited = Tabu(j,1:i-1);
            P = zeros(1,CityNum);%%初始化选择各城市的概率
            %%计算访问各个城市的概率
            for k = 1:CityNum
                if isempty(find(visited == k,1))
                    P(k) = (PheromoneMatrix(visited(end),k)^Alpha)*(EtaMatrix(visited(end),k)^Beta);
                else
                    P(k) = 0;%%不可访问的城市概率为0；
                end
            end
            P = P/sum(P);
            
            P = cumsum(P);
            cityIndex = find(P>=rand);%%选择常用方法：轮盘赌选择法
            %%③禁忌表 ： 为了不让蚂蚁选择已经访问过的地方，采用禁忌表的形式来记录蚂蚁k当前所走过的地方。
            Tabu(j,i) = cityIndex(1);
        end
    end   	
     dis = zeros(AntNum,1);%%准备记录每只蚂蚁的路线长度
    %%开始计算每只蚂蚁本次迭代路线长度
    for i = 1:AntNum
        for j = 1:CityNum-1
            dis(i) = dis(i) + DisMatrix(Tabu(i,j),Tabu(i,j+1));
        end
        dis(i) = dis(i) + DisMatrix(CityNum,1);
    end
   % 求本次迭代最优解或全局最优解在蚂蚁系统中不需要
    disMin = min(dis);
    routeIndex = find(dis==disMin);
    bestRoute(count,:) = Tabu(routeIndex(1),:);
    bestDistance(count) = disMin; 
     %%④信息素更新 ： 信息素挥发+信息素释放
    deltaPhe = zeros(CityNum,CityNum);
    for i = 1:AntNum
        for j = 1:CityNum-1
            deltaPhe(Tabu(i,j),Tabu(i,j+1)) = deltaPhe(Tabu(i,j),Tabu(i,j+1)) + Q/dis(i);
        end
        deltaPhe(Tabu(i,CityNum),Tabu(i,1)) = deltaPhe(Tabu(i,CityNum),Tabu(i,1)) + Q/dis(i);%%从终点到起点
    end
     PheromoneMatrix = (1 - Rho).* PheromoneMatrix + deltaPhe;
    %%⑤蚂蚁完成一次循环后，清空禁忌表，重新回到初始地点，准备下一次周游（循环）。
    Tabu = zeros(AntNum,CityNum);
end

resultDistance =  min(bestDistance);%%求全局最优解，最短路径距离
bestRouteIndex = find(bestDistance == resultDistance)
resultRoute = bestRoute(bestRouteIndex(1),:);%%求全局最优解，最短路径索引

R = resultRoute;
C = Cities;
N=length(R);
scatter(C(:,1),C(:,2));
 plot([C(R(1),1),C(R(N),1)],[C(R(1),2),C(R(N),2)],'g')
 hold on
for ii=2:N
    plot([C(R(ii-1),1),C(R(ii),1)],[C(R(ii-1),2),C(R(ii),2)],'g')
     hold on
end
title('旅行商问题优化结果 ');

minDis = 425.7183

%%简单路径规划问题%%
%%算法：蚁群算法（蚂蚁系统+蚁周模型）%%

%%算法介绍：
%%①初始化 ：初始化 ： 初始时刻，m只蚂蚁随机放置。在这个问题中，m只蚂蚁均放在起始点。
%%②状态转移 ： 蚂蚁k(k = 1,2,...m)按照随机比例规则选择下一步要转移的地点。
%%③禁忌表 ： 为了不让蚂蚁选择已经访问过的地方，采用禁忌表的形式来记录蚂蚁k当前所走过的地方。
%%④信息素更新 ： 信息素挥发+信息素释放
%%⑤蚂蚁完成一次循环后，清空禁忌表，重新回到初始地点，准备下一次出发。

clear all;
clc;
AntNum = 50;%%蚂蚁数量
Alpha = 1;%%信息启发因此α∈[0,5]   
Beta = 3;%%期望启发因子β∈[0,5]
Rho = 0.5;%%信息素挥发因子ρ∈[0.1,0.99]
Q = 1;%%蚁周模型信息素更新公式中参数Q∈[10,10000]
IterationTimes = 300;%%迭代（iteration）次数

%%1表示障碍物，0表示可以通过%%
Map = [0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0;
     0 1 1 1 0 0 1 1 1 0 1 1 1 1 0 0 0 0 0 0;
     0 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0;
     0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0;
     0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0;
     0 0 0 0 0 0 0 1 1 1 1 1 1 1 0 0 0 0 0 0;
     0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0; 
     0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0;
     1 1 1 1 0 0 0 0 0 0 0 1 1 1 0 1 1 1 1 0;
     1 1 1 1 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0;
     0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 0 1 1 0;
     0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0;
     0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0;
     0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0;
     ];
[row,column] = size(Map);
tauMatrix = ones(row*column,row*column);%%初始化信息素矩阵
%tauMatrix = 8 .* tauMatrix;
startPoint = [1,1];
finalPoint = [row,column];
D = G2D(Map);
N = size(D,1);  %%像素的个数
a = 1;    %像素边长，用于判断点坐标
startPointX = a * (startPoint(1) - 0.5);
startPointY = a * (startPoint(2) - 0.5);
finalPointX = a * (finalPoint(1) - 0.5);
finalPointY = a * (finalPoint(2) - 0.5);

start = (startPoint(1) - 1)*column + startPoint(2);
final = (finalPoint(1) - 1)*column + finalPoint(2);

Eta = zeros(N);%%启发信息，每个点到终点的距离的导数，蚂蚁倾向于走离终点近的点
for i = 1 : N
    selfX = a * (mod(i,row) - 0.5);             %% ---------→x
    if selfX == -0.5                            %%|
        selfX = a * (row - 0.5);                %%|
    end                                         %%|
    selfY = a * (ceil(i/row) - 0.5);            %%↓ y
    if i ~= final
        Eta(i) = 1/(((selfX - finalPointX)^2 + (selfY - finalPointY)^2)^0.5);
    else
        Eta(i) = 100;
    end
end

tabuMatrix = ones(AntNum,N);  %% 1 可达， 0 不可达

routes = cell(IterationTimes,AntNum);%%记录每次迭代每只蚂蚁的路径
routesDistance = zeros(IterationTimes,AntNum);
minij = inf;
mini = 0;
minj = 0;
%迭代开始
for i = 1:IterationTimes
    for j = 1:AntNum
        %%①初始化 ：初始化 ： 初始时刻，m只蚂蚁随机放置。在这个问题中，m只蚂蚁均放在起始点。
        position = start;
        path = start;%%记录本次迭代蚂蚁j的路径
        distance = 0;%%记录本次迭代蚂蚁j的路径距离；
        tabuMatrix(j,start) = 0;%%排除初始点
        
	%%TSP中除了禁忌表中的任意顶点都可以到达，allowedk = U - tabuk
        %%但这个问题中只有相邻八个像素可达，故要先找出八个像素
        %%并查看他们是否在禁忌表中，若在，则将邻接矩阵相应位置设置为0（不可达）；
        DD = D;%%每只蚂蚁有自己的一张邻接矩阵
        DW = DD(start,:);
        
	newIndex = find(DW);
        indexLength = length(newIndex);

	while position~=final && indexLength>=1%%当蚂蚁走到终点或蚂蚁无路可走的时候停止循环
            p = zeros(1,indexLength);
            %%②状态转移 ： 蚂蚁k(k = 1,2,...m)按照随机比例规则选择下一步要转移的地点。
            for k = 1:indexLength
                p(k) = (tauMatrix(position,newIndex(k))^Alpha + Eta(newIndex(k))^Beta);
            end
            p = p./sum(p);
            %%轮盘赌选择法
            p = cumsum(p);
            toVisitIndex = find(p>=rand);
            toVisit = newIndex(toVisitIndex(1));
            %%记录路径并移动到下一个点
            path = [path,toVisit];
            distance = distance + DD(position,toVisit);
            position = toVisit;
            %%重新寻找可到达区域
            DW = D(position,:);
            index = find(DW);
            %%③禁忌表 ： 为了不让蚂蚁选择已经访问过的地方，采用禁忌表的形式来记录蚂蚁k当前所走过的地方。
            for c = 1:length(index)
                if tabuMatrix(j,index(c)) == 0
                    %DD(position,index(k)) = 0;
                    %DD(index(k),position) = 0;
                    DW(index(c)) = 0;
                end
            end
            tabuMatrix(j,position) = 0;
            newIndex = find(DW);
            indexLength = length(newIndex);
        end
        %%此时蚂蚁已经走到终点或走到死角
        %%记录本次迭代蚂蚁j的路径
        routes{i,j} = path;
        if path(end) == final
            routesDistance(i,j) = distance;
            if distance < minij
                mini = i;
                minj = j;
                minij = distance;
            end
        else
            routesDistance(i,j) = 0;
        end
    end
    %%此时每只蚂蚁都走完了，完成了一次迭代
    %%④信息素更新 ： 信息素挥发+信息素释放(蚁周模型)
    if mini~=0&&minj~=0%%如果存在有到达终点的路径
        delta = zeros(row*column,row*column);
        rout = routes{mini,minj};
        count = length(rout) - 1;
        L = routesDistance(mini,minj);
        for s = 1:count
            x = rout(s);
            y = rout(s+1);
            delta(x,y) = Q/L;
            delta(y,x) = Q/L;
        end
    tauMatrix = (1 - Rho).* tauMatrix + delta;
    end
%%⑤蚂蚁完成一次循环后，清空禁忌表，重新回到初始地点，准备下一次出发。
    tabuMatrix = ones(AntNum,N);
end

%%绘制爬行图
figure(1)
axis([0,row,0,column]);
for i = 1:row
    for j = 1:column
        if Map(i,j)==1
            x1 = j - 1;y1 = row - i;
            x2 = j;y2 = row - i;
            x3 = j;y3 = row - i + 1;
            x4 = j - 1;y4 = row - i + 1;
            fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]);
            hold on
        else
            x1 = j - 1;y1 = row - i;
            x2 = j;y2 = row - i;
            x3 = j;y3 = row - i + 1;
            x4 = j - 1;y4 = row - i + 1;
            fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);
            hold on
        end
    end
end
title('机器人运动轨迹');
xlabel('坐标x');
ylabel('坐标y');
routLength = length(rout);
rx = rout;
ry = rout;
for i = 1:routLength
    rx(i) = a *(mod(rout(i),row) - 0.5);
    if rx(i) == -0.5
        rx(i) = a * (row - 0.5);
    end
    ry(i) = a*(row + 0.5 - ceil(rout(i)/row));
end
plot(rx,ry);
bestDistance = routesDistance(mini,minj);

%%由图生成row^2个像素与row^2个像素的邻接矩阵
function D = G2D(G) 
    [row,column] = size(G);
    D = zeros(row*column,row*column);
    for i = 1:row
        for j = 1:column
            if G(i,j)==0 %%此点不是障碍物
                %%遍历整个图row^column个像素，寻找与他八联通的八个像素
                for m = 1:row
                    for n = 1:column
                        if G(m,n)==0 %%如果像素不是障碍物
                            im = abs(i - m);
                            jn = abs(j - n);
                            if im+jn==1||(im==1&&jn==1)  %%如果在上下左右和斜着的八个方向
                         %%则设置邻接矩阵的权值
                            D((i - 1) * row + j,(m - 1) * row + n) = (im + jn)^0.5;
                            end
                        end
                    end
                end
            end
        end
    end
end

当解决有障碍物的路径规划问题上，我一开始出现了

这种一看就不对的图像，最终我观察发现解收敛太快，于是我减小了Q的值，从1000变为了1，最终便有了良好的结果。

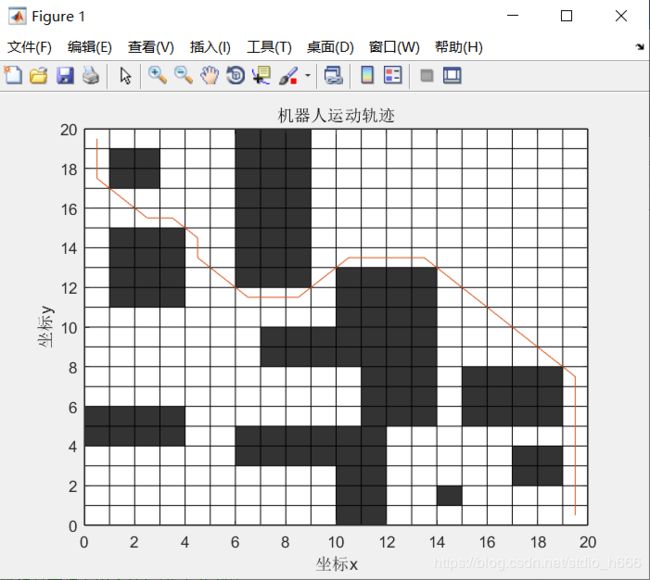
大量仿真实验发现，蚂蚁系统在解决小规模TSP问题时性能尚可，能较快的发现最优解，但随着测试问题规模的扩大，蚂蚁系统算法的性能下降的比较严重，容易出现停滞现象，因此出现了针对其缺点的改进算法。
在智能优化算法之蚁群算法（2）中详细讲解
2. 精英蚂蚁系统
3. 最大-最小蚂蚁系统
4. 基于排序的蚁群算法
5. 蚁群系统