LeetCode

应做未做

28.实现 strStr()
31.长度最小的子数组
32.用 Rand7() 实现 Rand10()
面试题 17.13. 恢复空格
312.戳气球

未弄懂

• 378.有序矩阵中第K小的元素 => 官方二分查找的答案中如何保证最终返回的结果是正确的??
• 478.在圆内随机生成点 => 拒绝抽样的统一思路？？

经典题+易错题

• 218.天际线问题 => 回看自己最初的扫描线算法,边界条件很多!! + 一题多解法
• 148.排序链表=> 二路归并(注意数组的话无法实现空间O(1)，自顶向下也无法实现空间O(1)，此题只能自底向上)
  350.两个数组的交集 II => 想到hash很容易，但是很难考虑到时空开销更小的方法
  206.反转链表 => 简单但是不容易理清楚，难以写出简洁的答案!!(迭代和递归两种解法，迭代循环外只需定义两个指针)

一、长见识的方法

• 前缀和+状态压缩=>1371.每个元音包含偶数次的最长子字符串
• 中心扩展法 => 5.最长回文子串
• 判断两个区间是否可以合并 => 57.插入区间
• 顺时针扫描矩阵=> 29. 顺时针打印矩阵
• Boyer-Moore 投票算法 => 169. 多数元素
• 识别排序数组中两个交换元素 => 99. 恢复二叉搜索树
• Morris 中序遍历 => 99. 恢复二叉搜索树(相比普通的递归中序遍历的优点在于其空间复杂度为O(1))
• 判断回文数时只反转一半数字 => 9. 回文数
• 单调栈
  739.每日温度； 42.接雨水； 1014.最佳观光组合；84. 柱状图中最大的矩形
• 双指针法 => 15.三数之和
• 双重二分查找 => 1300. 转变数组后最接近目标值的数组和
• 空间冗余以减少特殊判断
  718.最长重复子数组; 174.地下城游戏
• 最小堆完成k路归并排序 => 378. 有序矩阵中第K小的元素
• 扫描线算法+set => 218. 天际线问题
• 时间O(nlogn)空间O(1)的链表排序方法 => 148. 排序链表(只能自底向上)
• 不使用循环颠倒二进制位 => 190.颠倒二进制位
• 倒着dp => 174.地下城游戏
• 滚动数组优化空间 =>97.交错字符串

二、杂七杂八积累

• 注意对输入值特殊情况的排除:0、负数、空指针等

• 递归有很多重复计算，考虑使用动态规划(如斐波那契数列)

• 时间O(n)的排序=>通常针对数字范围小,使用hash

• 部分排序的数组也可能使用二分查找=>剑指 “旋转数组的最小数字”

• n&(n-1)：相当于将n的最右边的1变成0

• 通过x&1代替%判断x的奇偶性，从而提高计算效率！

• 如果指定了要删除的链表节点p，则O(1)的解法:交换p和后继位置，删除后继

• 当一个指针一次遍历链表无法解决问题，尝试使用两个相隔固定距离的指针(链表中倒数第k个节点)

• 查找一个未排序数组的中位数，不一定需要对整个数组排序，也可以使用partition用于寻找中位数，O(n)

• 大数问题 => 数字转换成字符串

• 一个数字与自己异或，结果必为0：x^x=0,剑指"数组中只出现一次的数字"

• 九大排序算法？不稳定的排序算法

• lowbit函数
  目的：用来求一个数二进制表示中最低一位
  代码：

  int lowbit(int x){
  	return x & (-x);    //x+(-x)==0; 因此x与-x按位与，最低位必定为1，其他位为0
  }
  
  //或者
  int lowbit(int x){
  	return x-(x & (x-1)); // x&(x-1)相当于将x最低位的1变成0，所以...
  }
  

• k路归并排序可使用最小堆进行优化，不用操心某路已经遍历完的情况！=> 参考：最小堆实现k路归并

• 求两个数的中间值(l+r)/2 => l+(r-l)/2 以防止溢出

三、分类归纳整理

数组

1300.转变数组后最接近目标值的数组和 =>排序+二分查找
1014.最佳观光组合 => 单调栈思路、动态规划等都可以解决
41.缺失的第一个正数 => 利用题目中数据的特点，用给定的数组构哈希表
122.买卖股票的最佳时机 II
315.计算右侧小于当前元素的个数 => 树状数组

栈、队列

42.接雨水(注意对比84柱状图最大矩形)
103.二叉树的锯齿形层次遍历 => 两个栈实现
739.每日温度(与42解法类似)
71.简化路径 => 栈中存放什么容易被干扰
84. 柱状图中最大的矩形 => 单调栈(注意对比42接雨水)
225.用队列实现栈 => 注意解法1、2队列引用交换的方式提高效率!! 解法3不易想到

堆

837.新21点
215.数组中的第K个最大元素
1046. 最后一块石头的重量

字符串

面试题 16.18. 模式匹配 => 注意如何转换为二元一次方程
28. 实现 strStr() => 典型的KMP, 注意答案中的其它解法!!

哈希表

138.复制带随机指针的链表 => 注意空间O(1)的解法，新老节点交替模拟实现hash的效果
41.缺失的第一个正数 => 利用题目中数据的特点，用给定的数组构哈希表
350.两个数组的交集 II

树

95.不同的二叉搜索树 II
99.恢复二叉搜索树
103.二叉树的锯齿形层次遍历 => 两个栈实现
173. 二叉搜索树迭代器 => 树的中序非递归
208.实现 Trie (前缀树) => 字典树(前缀树)
174. 翻转对 => 树状数组
1028.从先序遍历还原二叉树 => 树的遍历(考虑如何通过栈实现)
175.将有序数组转换为二叉搜索树=>思考如何证明解法保证了二叉搜索树是平衡的
109.有序链表转换二叉搜索树(同175，只是数组变为链表，同时使用快慢指针)
112.路径总和 => DFS即可(适当考虑剪枝)
315.计算右侧小于当前元素的个数 => 树状数组
106.从中序与后序遍历序列构造二叉树
107.二叉树的层次遍历 II =>BFS/层序遍历
96.不同的二叉搜索树
211.添加与搜索单词 - 数据结构设计 => trie树
617.合并二叉树
1382.将二叉搜索树变平衡 => 同175(可以尝试使用AVL树的旋转)

图

126.单词接龙 II => 关键在于将题目建模为图思路，然后进行搜索!!!
210. 课程表 II => 拓扑排序
200.岛屿数量 => 图的遍历，连通图

并查集

990.等式方程的可满足性B=> 难点在于建模成并查集
130.被围绕的区域 => 注意dummyNode
200.岛屿数量

排序

215.数组中的第K个最大元素 => 快速排序思路，借助于partition
169.多数元素 => 可借助于partition
378. 有序矩阵中第K小的元素 => 归并排序
148. 排序链表 => 自底向上的二路归并

查找

1300.转变数组后最接近目标值的数组和 => 二分查找
378. 有序矩阵中第K小的元素 => 二分查找
29.两数相除 => 翻倍的思想，类似于二分查找
剑指 Offer 11. 旋转数组的最小数字 => 二分查找

贪心算法

57.插入区间
1288. 删除被覆盖区间
122. 买卖股票的最佳时机 II

位运算

136.只出现一次的数字 => 对比剑指offer类似的题目 (使用xor)
137.只出现一次的数字 II => 统计每个位出现的总次数
67. 二进制求和 => 可以位运算(迁移到不使用四则运算的整数加法)； 也可以直接模拟(注意答案中精简的写法!!)
190.颠倒二进制位 => 注意答案中不使用循环的解法

拓扑排序

210.课程表 II => 拓扑排序
1203.项目管理

递归

46.把数字翻译成字符串

动态规划

44.通配符匹配
1014.最佳观光组合
46.把数字翻译成字符串
32.最长有效括号 => 注意空间还能优化为O(1)
375. 猜数字大小 II => 极小化极大
376. 最长重复子数组 =>注意动态规划数组的冗余可减少边界判断!
62.不同路径
63.不同路径 II
309.最佳买卖股票时机含冷冻期 => 考虑每一个时刻的所有可能状态！ (顺便复习所有股票类题目)
174.地下城游戏
96.不同的二叉搜索树
97.交错字符串
312.戳气球

记忆化搜索

329.矩阵中的最长递增路径

分治法

241.为运算表达式设计优先级

回溯法

37.解数独

滑动窗口

718. 最长重复子数组
719. 最小覆盖子串 =>r指针用于延伸窗口，l指针用于压缩窗口

扫描线算法

1288.删除被覆盖区间

脑筋急转弯

面试题 16.11. 跳水板

数学归纳/找规律

1025.除数博弈

四、基础知识总结

4.1字符串

字符串匹配—KMP

• 概述
  KMP算法利用比较过的信息，主串上的指针 $i$ 不需要回溯，只需将子串向右滑动一个合适的位置和主串开始比较(这个合适的位置仅和子串本身的结构有关，与主串无关)

4.2树

并查集(待完善,时间复杂度分析)

• 基础理解
  常用于解决连通性问题

• 三个稍作
  1.init(s) => 将集合s中的每一个元素都初始化为只有一个单元素的子集合
  2.find(s,idx) => 查找对应下标的元素所在的集合，返回该集合对应的根节点下标
  3.union(root1, root2) => 将互不相交的集合root1和root2合并

• 代码(常规)

  #define SIZE 100
  int S[SIZE];               //双亲指针数组(下标对应元素，值对应父节点编号)，根节点的父节点编号为负数
  
  //初始化，每个元素自成一个集合
  void init(int S[]){
  	for(int i=0;i<size;i++)
  		S[i]=-1;
  }
  //查找，返回某个编号的节点所在集合的根节点的编号
  int find(int S[], int idx){
  	while(S[idx]>=0)                       //找到根节点时退出
  		idx=S[idx];
  	return idx;
  }
  
  //合并两个不相交的集合
  void unite(int S[],int root1, int root2){
  	//S[root1]+=S[root2];            =>若全部初始化为-1，此步骤可以用根节点的父节点值(负数)的绝对值表示集合元素个数 
  	S[root2]=root1;                  //将集合2合并到集合1下面
  	//S[find(idx2)]=find(idx1);      //如果输入的是要合并的两个元素，
  }
  

• 代码(路径压缩优化)

  class UnionFind {
      int[] parents;
  
      public UnionFind(int totalNodes) {
          parents = new int[totalNodes];
          // 每个结点初始化为一个集合，且父节点为他本身(方便路径压缩进行优化) 
          // <=> 对比常规代码此处的区别!!
          for (int i = 0; i < totalNodes; i++) {
              parents[i] = i;
          }
      }
  	//合并两个节点，合并连通区域是通过find来操作的, 即看这两个节点是不是在一个连通区域内.
      void union(int node1, int node2) {
          int root1 = find(node1);
          int root2 = find(node2);
          if (root1 != root2) {
              parents[root2] = root1;
          }
      }
      // 查找，注意使用了路径压缩，查找过程中修改树结构
      int find(int node) {
          while (parents[node] != node) {
              // 当前节点的父节点 指向父节点的父节点.
              // 保证一个连通区域最终的parents只有一个.
              parents[node] = parents[parents[node]];
              node = parents[node];
          }
  
          return node;
      }
  }
  

参考：990. 等式方程的可满足性

二叉树的遍历

• 先序

• 中序

• 后序

• 层序

• 中序非递归
  先中后根的三种遍历写法很简单，此处略去； 下面是常考的中序非递归

  void InOrder(BiTree T){
  	InitStack(S); BiTree p=T;         //p是遍历指针
  	while(p || !isEmpty(S)){
  		if(p){
  			while(p){                 // 向左走完!!
  				S.push(p); p=p->left;
  			}
  		}
  		else{
  			Pop(S,p); visit(p);   
  			p=p->right;              //向右走!!!
  		}
  	}
  }
  

例题：173. 二叉搜索树迭代器
中序遍历对比 <=> 二叉树的线索化

B树和B+树

字典树/前缀树/Trie

• 基础知识
  1.trie树结点示意图
  
  可见，trie树的层数就是单词长度+1(最后一层不存储指针)
  2.trie树常见的操作 => 插入、查找(键、键前缀)
  3.注意：trie树的叶子结点不对应任何数据，且isEnd标志为true

• 代码

  /*结点定义*/
  class TrieNode {
      private TrieNode[] links;             //每个结点包含R个指向下层结点的指针
      private final int R = 26;
      private boolean isEnd;              //标志当前结点是否为一个键的末尾(一个长单词中途可能也会遇到isEnd==true的情况)
  
      public TrieNode() {
          links = new TrieNode[R];
      }
      
      public boolean containsKey(char ch) {
          return links[ch -'a'] != null;
      }
      public TrieNode get(char ch) {
          return links[ch -'a'];
      }
      public void put(char ch, TrieNode node) {
          links[ch -'a'] = node;
      }
      public void setEnd() {
          isEnd = true;
      }
      public boolean isEnd() {
          return isEnd;
      }
  }
  
  /*字典树*/
  class Trie {
      private TrieNode root;
  
      public Trie() {
          root = new TrieNode();
      }
      //插入
      public void insert(String word) {
          TrieNode node = root;
          for (int i = 0; i < word.length(); i++) {
              char currentChar = word.charAt(i);
              if (!node.containsKey(currentChar)) {
                  node.put(currentChar, new TrieNode());
              }
              node = node.get(currentChar);
          }
          node.setEnd();
      }
  	//用于查找整个键或者键前缀
      private TrieNode searchPrefix(String word) {
          TrieNode node = root;
          for (int i = 0; i < word.length(); i++) {
             char curLetter = word.charAt(i);
             if (node.containsKey(curLetter)) {
                 node = node.get(curLetter);
             } else {
                 return null;
             }
          }
          return node;
  	}
  	// 查找整个键
      public boolean search(String word) {
         TrieNode node = searchPrefix(word);
         return node != null && node.isEnd();
      }
      //查找键前缀
  	public boolean startsWith(String prefix) {
          TrieNode node = searchPrefix(prefix);
          return node != null;
  	}	
  }
  

  分析：时间复杂度O(m)，m代表键长； 空间O(1)
  与平衡树、哈希表相比而言的优点…
  详情参考：字典树
  例题：211. 添加与搜索单词 - 数据结构设计

树状数组/二叉索引树

• 基本原理
  主要用于解决区间和、前缀和等问题
  
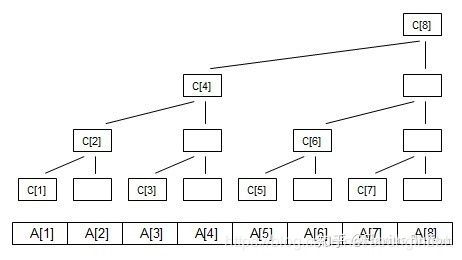
  (上图只是为了方便理解，空白结点在树状数组中并不存在，更恰当的图参考：树状数组详解)
  原数组为A[1]…A[8]； 对应的树状数组为C[1]…C[8]；原数组前缀和为SUM[1]…SUM[8]，注意下标都是从1开始!!! 观察可知：

C[1]=A[1]	SUM[1]=C[1]
C[2]=A[1]+A[2]	SUM[2]=C[2]
C[3]=A[3]	SUM[3]=C[3]+C[2]
C[4]=A[1]+A[2]+A[3]+A[4]	SUM[4]=C[4]
C[5]=A[5]	SUM[5]=C[5]+C[4]
C[6]=A[5] +A[6]	SUM[6]=C[6]+C[4]
C[7]=A[7]	SUM[7]=C[7]+C[6]+C[4]
C[8]=A[1]+A[2]...A[8]	SUM[8]=C[8]

=>规律：
1. $C[i]=A[i-2^k+1]+A[i-2^k+2]...+A[i]$，k满足 $lowbit(i)=2^k$
2.$SUM[i]=C[i]+C[i-lowbit(i)]+C[(i-lowbit(i))-lowbit(i-lowbit(i))]...每个累加项都是向下递归所得$
3.设节点编号为$i$，那么该节点维护的值是$[i-lowbit(i)+1,i]$这个区间的和(即规律1) => 简单的线段树

• 代码
  树状数组最基本的操作有两个：单点更新和区间查询

  // 计算lowbit
  int lowbit(int x){
  	return x & (-x);
  	//或者 return x -(x&(x-1));
  }
  
  //单点更新，原数组A[idx]加上
  void update(int idx, int incr){
  	A[idx]+=incr;
  	// 实际上这是不断往上查找父节点的过程!!
  	for(int i=idx; i<=n; i+=lowbit(i))       
  		C[i]+=incr;
  }
  
  //区间查询,求A[1]...A[idx]的和
  int sum(int idx){
  	int res=0;
  	for(int i=idx;i>0;i-=lowbit(i))
  		res+=C[i];
  	return res;
  }
  

  通过lowbit即可实现查找、更新的原理比较难以理解，参考知乎体会体会
  修改和查询的复杂度都是O(logN)
  例题：493. 翻转对
  315. 计算右侧小于当前元素的个数(注意离散化的过程)

线段树

AVL树(代码未完成)

• 概念基础
  AVL树既是一棵平衡树(高度差不超过1)； 又是一棵二叉搜索树(有序)
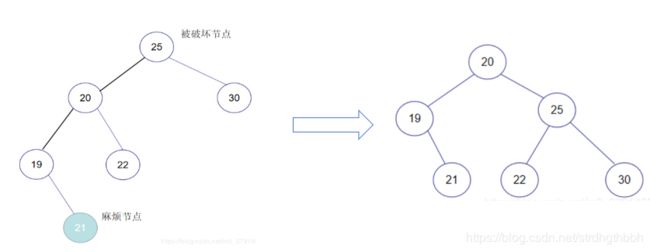
  根据插入节点的位置相对于最小不平衡子树的位置，调整为平衡树的情况可分为四类：LL(左孩子的左子树插入)、RR(右孩子的右子树插入)、LR(左孩子的右子树插入)、RL(右孩子的左子树插入) => 具体调整方案文字叙述比较枯燥，实际上看图就能明白
  以下多数内容参考自：数据结构之——平衡二叉树（内容详解）
• LL型
  调整方案 => 右旋：
  

示例：

代码：

```cpp
在这里插入代码片
```

• RR型
  解决方案 => 左旋：
  
  示例：
  
  代码：

  在这里插入代码片
  

• LR型
  解决方案 => 先对最小不平衡子树的左子树上的节点右旋，再对最小不平衡子树进行左旋
  示例：
  
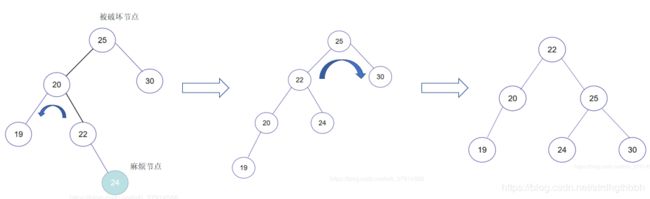
  代码：

  在这里插入代码片
  

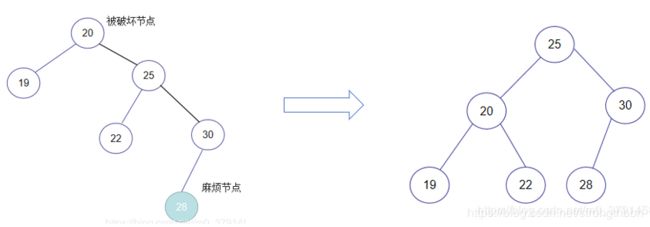
• RL型
  解决方案 => 先对最小不平衡子树的右子树上的节点进行左旋，然后对最小不平衡子树进行右旋
  示例：
  
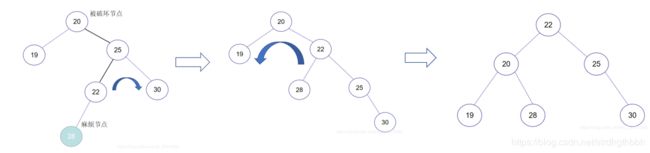
  代码：

  在这里插入代码片
  

4.3图

图的遍历

本质上就是在树的先根遍历、层序遍历的基础上增加visited数组!

• DFS
  代码：

  bool visited[MAX_VERTEX_NUM];
  void DFSTraverse(Graph  G){
  	for(v=0; v<G.vexnum; v++)      //初始化visited数组
  		visited[v]=false;
  	for(v=0; v<G.vexnum; v++)     //这个循环保证能遍历完非连通图！！！
  		if(!visited[v]) DFS(G,v);
  }
  void DFS(Graph G, int v){
  	visit(v);
  	visited[v]=true;             //设置已访问
  	for(w=FirstNeighbor(G,v); w>=0; w=NextBeighbor(G,v,w))
  		if(!visited[w]) DFS(G,w);   //w是v尚未访问的邻接点
  }
  

  分析：
  1.空间复杂度：O(n) => 递归，需要借助递归工作栈
  2.时间复杂度：邻接表：O(|V|+|E|) <=>邻接矩阵O(|V^2|)
  3.对于同一个图，由于邻接表可能不同，因此DFS遍历序列可能不同(矩阵则同)

• BFS
  代码： 借助队列，略…
  分析：
  1.空间复杂度：O(n) => 需要使用队列
  2.时间复杂度：邻接表：O(|V|+|E|) <=>邻接矩阵O(|V^2|)
  3.对于同一个图，由于邻接表可能不同，因此BFS遍历序列可能不同(矩阵则同)
  4.BFS可用于求解非带权图的单元最短路径

拓扑排序

• 思路：每次选取DAG中没有前驱的节点即可。这个过程其实就是在遍历图，因此可分为DFS解法和BFS解法，下面以DFS为例(BFS只需将栈改为队列即可)
• 代码(DFS)=> 此为非递归写法，也可写为递归

  TopologicalSort(Graph G){
  	InitStack(S);
  	for(injt i=0;i<G.vexnum;i++)
  		if(indegree[i]==0)                   //所有入度为0的顶点入栈
  			Push(S,i);
  	int cnt=0;                               //记录当前已经输出的顶点数
  	while(!IsEmpty(S)){
  		Pop(S,i);
  		print(i);                            //输出顶点i
  		cnt++;
  		for(p=G.vertices[i].firstarc;p=p->nextarc){
  			v=p->adjvec;
  			if(!(--indegree[v]))           //去掉顶点i后，与i相邻的入度为0的顶点入栈
  				Push(S,v);
  		}
  	}
  	if(cnt<G.vexnum) return false;          //有回路
  	return true;
  	
  }
  

  若是邻接表；则时间O(|V|+|E|) ； 若是邻接矩阵，则时间O(|V|^2)
  空间O(|V|)
  为什么此处遍历图没有使用visited[]数组？ => 因为这是有向无环图(DAG)，不可能回到已经遍历过的节点
  例题：210. 课程表 II => 拓扑排序
  双重拓扑排序：1203. 项目管理
  

二分图

• 概念
  如果我们能将一个图的节点集合分割成两个独立的子集A和B，并使图中的每一条边的两个节点一个来自A集合，一个来自B集合，我们就将这个图称为二分图。
• 二分图的判断
  染色法：如果给定的无向图连通，那么我们就可以任选一个节点开始，给它染成红色。随后我们对整个图进行遍历，将该节点直接相连的所有节点染成绿色，表示这些节点不能与起始节点属于同一个集合。我们再将这些绿色节点直接相连的所有节点染成红色，以此类推，直到无向图中的每个节点均被染色。 => 因此关键就是图的遍历问题，空间复杂度O(|V|)，时间复杂度根据图的存储结构为O(|V|+|E|)或者O(|V|^2)
  并查集：我们知道如果是二分图的话，那么图中每个顶点的所有邻接点都应该属于同一集合，且不与顶点处于同一集合。因此我们可以使用并查集来解决这个问题，我们遍历图中每个顶点，将当前顶点的所有邻接点进行合并，并判断这些邻接点中是否存在某一邻接点已经和当前顶点处于同一个集合中了，若是，则说明不是二分图。
  相关题目：785. 判断二分图
• 二分图匹配

4.4位运算

位运算常用技巧

位运算进行整数加法

	int add(int x, int y){
		int answer; int carry;
		while(y){
			answer=x^y;               // x^y的结果是不考虑进位的和
			carry=(x&y) << 1;         // (x&y)产生进位,(x&y)<<1是进位的值(进位补偿)
			x=answer; y=carry;       //由上面注释：x+y=x^y + (x&y)<<1 => 由于不使用加法，此处通过循环继续迭代下去完成x^y 和 (x&y)<<1的求和
		}
		return x;
	}

4.5排序

二路归并

• 自顶向下
  采用递归方式(可转换为用栈)
  代码参考：二路归并排序
  时间复杂度：每一轮归并所有数字都会被遍历到O(n)，共log2n轮 => O(nlog2n)
  空间复杂度：需要一个数组来暂存中间元素,O(n)； 递归栈的空间复杂度O(log2n)
• 自底向上
  采用迭代方式
  代码参考归并排序-自底向上的二路归并
  时间复杂度：每轮归并所有元素都被遍历到O(n)，共log2n轮 => O(nlog2n)
  空间复杂度：需要一个数组暂存O(n)，但是不需要栈空间!!
• 空间复杂度O(1)的二路归并
  当要排序的是链表时，只需要修改指针，不用暂存元素；此时若使用自底向上的二路归并，也不需使用栈，故时间复杂度O(1) => 148. 排序链表
• k路归并排序
  使用小根堆/优先队列辅助排序更方便 =>

4.6随机算法

蓄水池抽样算法

• 目的
  在大数据场景中，如果想从数据量很大的n个数中以相等的概率随机选取k个数(假设总数为n，则每个数被选中的概率都应该是$k/n$)。其中n未知或者很大，无法把所有数据直接加载到内存，从而不能对数据进行随机读取，我们需要在对数据的一次遍历中完成等概率抽取k个数的任务
• 算法
  1.先读取k个数作为蓄水池
  2.从$i=k+1$开始，以$k/i$的概率选取第$i$个数；若选取了第$i$个数，则用它随机替换掉蓄水池中原来的某个数
  3.重复2的步骤，直到对所有数据完成一次遍历，最终蓄水池中的数据就是随机抽样的结果
• 证明
  $P1(第i个数最终在蓄水池中)=P2(第i个数被选进蓄水池)\ast P3(第i个数没有被后面的数字从蓄水池中替换出来)$
  其中，$P2=\frac{k}{i}$
  $P3=P(后面的元素没有被选择)+P(后面的元素被选择但是替换出来的不是第i个数)$
  => $P3=[(\frac{i+1-k}{i+1}+\frac{k}{i+1}(1-\frac{1}{k}))\times (\frac{i+2-k}{i+2}+\frac{k}{i+2}(1-\frac{1}{k}))...(\frac{n-k}{n}+\frac{k}{n}(1-\frac{1}{k}))]=\frac{i}{n}$
  综上：$P1=p2\times P3=\frac{k}{n}$，即每个数字最终被抽到的概率都是相同的
• 代码

  choice = file[1:k]
  i = k+1
  while file[i] != None
      r = random(1,k);
      with probability k/i:
          choice[r] = choice[i] 
      i++
  print choice
  

• 特例
  当k=1时的特殊情况，见：382. 链表随机节点

洗牌算法

拒绝抽样

做题领会 => 478. 在圆内随机生成点

470. 用 Rand7() 实现 Rand10()

4.7计算几何

极角排序

• 概念
  
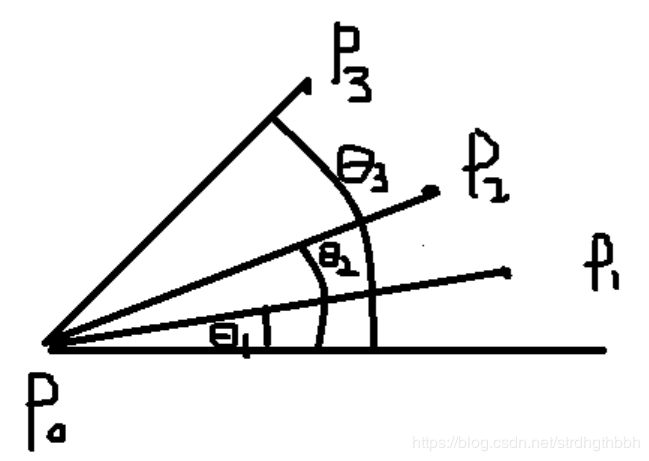
  极角排序就是对于某个给定点(P0)，根据其他点相对于给定点的角度大小(θ1、θ2、θ3)，对其他点进行排序(排序结果为P1、P2、P3)
  常用方法有：atan2、叉积法等，下文仅讲解叉积法原理
• 叉积法
  
  注：不用纠结象限问题，不管所有点处于哪个象限，上述算法都是正确的

   // 以p为基准,根据返回值的正负判断q 、r的大小
   int orientation(Point p, Point q, Point r) {
   	//返回叉积结果
      return (q.y - p.y) * (r.x - q.x) - (q.x - p.x) * (r.y - q.y);
  }
  

凸包问题

• 问题描述
  给定一堆(二维)坐标点，找出能包围所有点的最小凸多边形(对应的点)
• 极边法
  思路：对于两点连成的线段，如果是凸多边形的边，则其余所有点都在该线段的一侧 => 遍历所有线段O(n^2)，判断是否为凸多边形的边O(n)，总时间复杂度为O(n ^3)； 类似的还有极点法等
• Jarvis 算法
  1.先找到一个极点(通常取x坐标最小的点 => 方便逆时针找点)
  2.以此极点p为基准，遍历所有点，找到一个极角最小的点q，则q必定是极点
  3.将p更新为q，重复步骤2，直到p回到步骤1选取的点
  注意：实现算法时需要处理三个点在同一条线上的特殊情况
  复杂度：时间O(n*m)，n是点总数，m是极点个数
  代码参考：587. 安装栅栏
• Graham扫描算法
  参考：587. 安装栅栏

扫描线算法

不是一种具体的算法，而是一种思想

• 相关题目
  218.天际线问题

4.x记忆化搜索

=> 记忆化搜索与动态规划比较类似，都是存储了中间计算结果，只是记忆化很多时候使用了递归/深度优先搜索!!!
动态规划要求按照拓扑顺序解决子问题。对于很多问题，拓扑顺序与自然秩序一致。而对于那些并非如此的问题，需要首先执行拓扑排序。因此,对于复杂拓扑问题（如329），使用记忆化搜索通常是更容易更好的选择。

4.x卡特兰数