图像频率域分析之傅里叶变换
文章目录
- 傅里叶变换基础
- 傅里叶级数
- 傅里叶积分
- 傅里叶变换
- 一维连续傅里叶变换
- 一维离散傅里叶变换
- 二维离散傅里叶变换
- 正变换
- 反变换
- 卷积
- 卷积定理
- 数字图像DFT
- 空间域和频域
- 图像频域滤波
- 基本步骤
- 图像频率特性分析
- 图像滤波实践
- Python分析
- C++分析
- 源代码
- 参考资料
傅里叶变换基础
傅里叶级数
法国数学家傅里叶发现,任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示(选择正弦函数与余弦函数作为基函数是因为它们是正交的),即 任何周期信号都可以表示成一系列正弦信号的叠加
- 三角形式
f ( t ) = a 0 2 + ∑ k = 1 + ∞ [ a k c o s ( n ω t ) + b k s i n ( n ω t ) ] , a 0 2 = 1 T ∫ − T 2 T 2 f ( t ) d t f(t) = \frac{a_0}{2} + \sum_{k=1}^{+\infty} \big[ a_k cos (n \omega t) + b_k sin (n \omega t) \big], \quad \frac{a_0}{2} = \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) dt f(t)=2a0+k=1∑+∞[akcos(nωt)+bksin(nωt)],2a0=T1∫−2T2Tf(t)dt
- 复指数形式
f ( t ) = 1 T ∑ n = − ∞ + ∞ [ ∫ − T 2 T 2 f ( τ ) e − j ω n τ d τ ] e j ω n t f(t) = \frac{1}{T} \sum_{n=-\infty}^{+\infty} [ \int_{-\frac{T}{2}}^{\frac{T}{2}} f(\tau)e^{-j\omega_n\tau} d\tau ] e^{j\omega_nt} f(t)=T1n=−∞∑+∞[∫−2T2Tf(τ)e−jωnτdτ]ejωnt
基波角频率 ω = 2 π T \omega = \frac{2\pi}{T} ω=T2π , T T T 为 f ( t ) f(t) f(t) 的周期, j j j 为虚数单位
傅里叶积分
复指数形式
f ( t ) = 1 2 π ∫ − ∞ + ∞ [ ∫ − ∞ + ∞ f ( τ ) e − j ω τ d τ ] e j ω t d ω f(t) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} [ \int_{-\infty}^{+\infty} f(\tau)e^{-j\omega\tau} d\tau ] e^{j\omega t} d\omega f(t)=2π1∫−∞+∞[∫−∞+∞f(τ)e−jωτdτ]ejωtdω
傅里叶变换
一维连续傅里叶变换
正变换 为
F ( ω ) = ∫ − ∞ + ∞ f ( t ) e − j ω t d t F(\omega) = \int_{-\infty}^{+\infty} f(t) e^{-j\omega t} dt F(ω)=∫−∞+∞f(t)e−jωtdt
逆变换 为
f ( t ) = 1 2 π ∫ − ∞ + ∞ F ( ω ) e j ω t d ω f(t) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} F(\omega) e^{j\omega t} d\omega f(t)=2π1∫−∞+∞F(ω)ejωtdω
一维离散傅里叶变换
正变换 为
F ( u ) = ∑ x = 0 M − 1 f ( x ) e − j 2 π u x M F(u) = \sum_{x=0}^{M-1} f(x) e^{-j2\pi \frac{ux}{M}} F(u)=x=0∑M−1f(x)e−j2πMux
则
F ( 0 ) = ∑ x = 0 M − 1 f ( x ) F(0) = \sum_{x=0}^{M-1} f(x) F(0)=x=0∑M−1f(x)
反变换 为
f ( x ) = 1 M ∑ u = 0 M − 1 F ( u ) e j 2 π u x M f(x) = \frac{1}{M} \sum_{u=0}^{M-1} F(u) e^{j2\pi \frac{ux}{M}} f(x)=M1u=0∑M−1F(u)ej2πMux
对于反变换式前的系数 1 M \frac{1}{M} M1 ,也可放在正变换中,只要保证正变换与反变换之前的系数乘积为 1 M \frac{1}{M} M1 即可。
二维离散傅里叶变换
正变换
二维离散傅里叶变换:
F [ f ( x , y ) ] = F ( u , v ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) e − j 2 π ( u x M + v y N ) F[f(x,y)] = F(u,v) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x,y) e^{-j2\pi(\frac{ux}{M}+\frac{vy}{N})} F[f(x,y)]=F(u,v)=x=0∑M−1y=0∑N−1f(x,y)e−j2π(Mux+Nvy)
当 ( u , v ) (u,v) (u,v) 等于 ( 0 , 0 ) (0,0) (0,0) 时,直流分量 为:
F ( 0 , 0 ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) F(0,0) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x,y) F(0,0)=x=0∑M−1y=0∑N−1f(x,y)
幅度谱 为:
A ( u , v ) = ∣ F ( u , v ) ∣ = R e a l ( u , v ) 2 + I m a g e ( u , u ) 2 A(u,v) = |F(u,v)| = \sqrt{Real(u,v)^2 + Image(u,u)^2} A(u,v)=∣F(u,v)∣=Real(u,v)2+Image(u,u)2
功率谱 为:
P ( u , v ) = ∣ F ( u , v ) ∣ 2 = R e a l ( u , v ) 2 + I m a g e ( u , u ) 2 P(u,v) = |F(u,v)|^{2} = Real(u,v)^2 + Image(u,u)^2 P(u,v)=∣F(u,v)∣2=Real(u,v)2+Image(u,u)2
相位谱 为:
ϕ ( u , v ) = a r c t a n I m a g e ( u , v ) R e a l ( u , v ) \phi(u,v) = arctan \frac{Image(u,v)}{Real(u,v)} ϕ(u,v)=arctanReal(u,v)Image(u,v)
通过 幅度谱 和 相位谱,我们也能合成 其傅里叶变换(频谱):
F ( u , v ) = A ( u , v ) e j ϕ ( u , v ) = A ( c o s ϕ + j s i n ϕ ) (省略(u,v),应用 欧拉公式) = A c o s ϕ + j A s i n ϕ \begin{aligned} F(u,v) &= A(u,v)e^{j\phi(u,v)} \\ &= A( cos \phi + jsin \phi ) \quad \text{(省略(u,v),应用 欧拉公式)}\\ &= Acos\phi + jAsin\phi \end{aligned} F(u,v)=A(u,v)ejϕ(u,v)=A(cosϕ+jsinϕ)(省略(u,v),应用 欧拉公式)=Acosϕ+jAsinϕ
注意:
- 上面式子中的 j j j 为 虚数单位
- R e a l ( u , v ) Real(u,v) Real(u,v) 为 复数的 实部
- I m a g e ( u , v ) Image(u,v) Image(u,v) 为 复数的 虚部
反变换
f ( x , y ) = F − 1 ( u , v ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 F ( u , v ) e j 2 π ( u x M + v y N ) f(x,y) = F^{-1}(u,v) = \frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F(u,v) e^{j2\pi(\frac{ux}{M}+\frac{vy}{N})} f(x,y)=F−1(u,v)=MN1u=0∑M−1v=0∑N−1F(u,v)ej2π(Mux+Nvy)
卷积
∫ − ∞ + ∞ f 1 ( τ ) f 2 ( t − τ ) d τ = f 1 ( t ) ∗ f 2 ( t ) \int_{-\infty}^{+\infty} f_1(\tau)f_2(t-\tau) d\tau = f_1(t) * f_2(t) ∫−∞+∞f1(τ)f2(t−τ)dτ=f1(t)∗f2(t)
卷积定理
函数卷积的傅立叶变换是函数傅立叶变换的乘积
- 时域卷积定理:时域内的卷积对应频域内的乘积
F [ f 1 ( t ) ∗ f 2 ( t ) ] = F 1 ( ω ) ⋅ F 2 ( ω ) F[f_1(t) * f_2(t)] = F_1(\omega) \cdot F_2(\omega) F[f1(t)∗f2(t)]=F1(ω)⋅F2(ω)
- 频域卷积定理:频域内的卷积对应时域内的乘积
F [ f 1 ( t ) ⋅ f 2 ( t ) ] = 1 2 π F 1 ( ω ) ∗ F 2 ( ω ) F[f_1(t) \cdot f_2(t)] = \frac{1}{2\pi} F_1(\omega) * F_2(\omega) F[f1(t)⋅f2(t)]=2π1F1(ω)∗F2(ω)
数字图像DFT
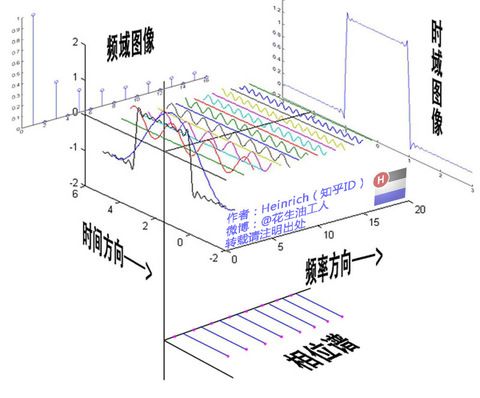
借用知乎大神Heinrich的一张图,来个感性认识:
空间域和频域
- 空间域:在图像处理中,时域可以理解为 空间域 或者 图像空间,处理对象为图像像元;
- 频域:以 空间频率 为自变量描述图像的特征,可以将一幅图像像元值在空间上的变化分解为具有不同振幅、空间频率和相位的简振函数的线性叠加,图像中各种空间频率成分的组成和分布称为 图像频谱
空间域与频域可互相转换,对图像施行 二维离散傅立叶变换 或 小波变换 ,可以将图像由空间域转换到频域;通过 对应的反变换 又可转换回空间域图像,即人可以直接识别的图像。
图像频域滤波
二维数字图像的滤波主要分为 空间域滤波 和 频域滤波:
-
空间域滤波: 用各种模板直接与图像进行 卷积运算,实现对图像的处理,这种方法直接对图像空间操作,操作简单
-
频域滤波: 在实现某些图像处理的时候,频域的处理比空间域更简单;对于在空间域上的数字图像,根据 卷积定理 可以通过 傅立叶变换 将 空域卷积滤波 变换为 频域滤波,然后再将频域滤波处理后的图像 反变换 回空间域
基本步骤
图像频域滤波步骤为(频谱图中心化):
- 计算 原始图像 f ( x , y ) f(x,y) f(x,y) 的DFT,得到 频谱 F ( u , v ) F(u,v) F(u,v)
- 中心化:将频谱 F ( u , v ) F(u,v) F(u,v) 的零频点移动到频谱图的中心位置
- 计算 滤波器函数 H ( u , v ) H(u,v) H(u,v) 与 F ( u , v ) F(u,v) F(u,v) 的乘积 G ( u , v ) = F ( u , v ) ⋅ H ( u , v ) G(u,v) = F(u,v) \cdot H(u,v) G(u,v)=F(u,v)⋅H(u,v)
- 反中心化:将频谱 G ( u , v ) G(u,v) G(u,v) 的零频点移回到频谱图的左上角位置
- 计算上一步计算结果的 傅里叶反变换 g ( x , y ) g(x,y) g(x,y)
- 取 g ( x , y ) g(x,y) g(x,y) 的 实部 作为最终滤波后的结果图像
上面步骤是对 图像频谱 进行 中心变换;我们也可以先对 原始图像 进行 中心变换,再计算其 频谱图,滤波步骤如下(原始图中心化):
- 原始图像 f ( x , y ) f(x,y) f(x,y) 中心变换: f ( x , y ) ⋅ ( − 1 ) ( x + y ) f(x,y) \cdot (-1)^{(x+y)} f(x,y)⋅(−1)(x+y)
- 计算上一步计算结果的DFT,得到其 频谱 F ( u , v ) F(u,v) F(u,v)
- 计算 滤波器函数 H ( u , v ) H(u,v) H(u,v) 与 F ( u , v ) F(u,v) F(u,v) 的乘积 G ( u , v ) = F ( u , v ) ⋅ H ( u , v ) G(u,v) = F(u,v) \cdot H(u,v) G(u,v)=F(u,v)⋅H(u,v)
- 计算 G ( u , v ) G(u,v) G(u,v) 的 傅里叶反变换 g ( x , y ) g(x,y) g(x,y)
- 取 g ( x , y ) g(x,y) g(x,y) 的 实部
- 上一步计算结果 乘以 ( − 1 ) ( x + y ) (-1)^{(x+y)} (−1)(x+y) 作为最终滤波后的结果图像
滤波能否取得理想结果的关键取决于上面的 滤波器函数 H ( u , v ) H(u,v) H(u,v) 。
这时让我想到了《自动控制理论》中的 传递函数 G ( s ) G(s) G(s),定义为:初始条件为零的线性定常系统输出的拉普拉斯变换与输入的拉普拉斯变换之比。
下面以 控制论的思想 给出图像频域滤波的示意框图:
![]()
图像频率特性分析
频谱图上的每一个像素点都代表一个频率值,幅值由像素点亮度变码而得。对于一幅图像,图像信号的 频率特性 如下:
- 直流分量 表示预想的平均灰度
- 低频分量 代表了大面积背景区域和缓慢变化部分
- 高频分量 代表了它的边缘、细节、跳跃部分以及颗粒噪声
- 振幅 描述了图像灰度的亮度
- 相位 决定了图像是什么样子
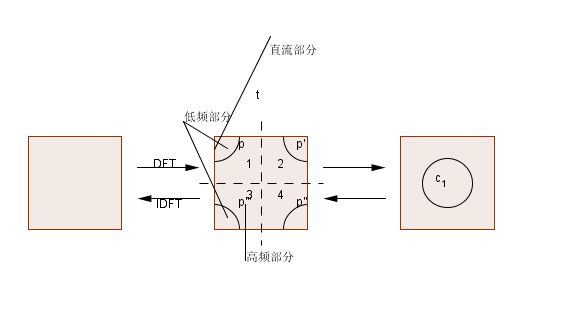
数字图像的二维离散傅立叶变换所得的结果的频域成分如下图所示,左上角是直流成分,变换结果四个角周围对应于低频成分,中央部分对应于高频部分
为了便于观察,常常采取 换位 方法使直流成分出现在窗口的中央(中心化),变换后中心为低频,向外是高频。
在频域,可以很方便的实现 图像的锐化和模糊:
- 截取频率的低频分量,对其作傅立叶反变换,得到的就是模糊后的图像,即 低通滤波
- 截取频率的高频分量,对其作傅立叶反变换,得到的就是锐化后的图像,即 高通滤波
图像滤波实践
下面,我们以 lena.bmp(点此下载) 图像进行滤波实践。
Python分析
(1)加载图像,并转换为 灰度图 为
![]()
(2)对其 快速傅里叶变换,并经过 中心变换,得到 频率谱 和 相位谱
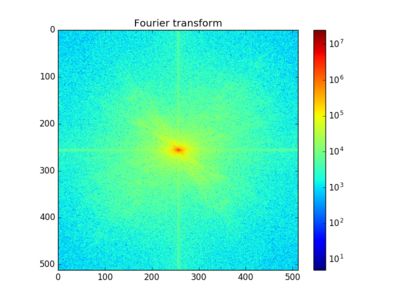
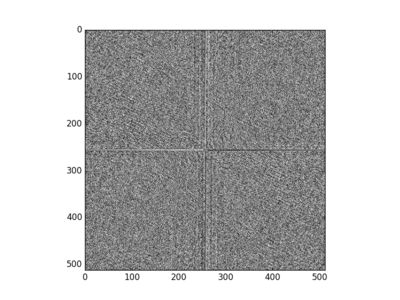
(3)分别截取 频谱图 的 低频部分(中间部分) 和 高频分量(四周部分)
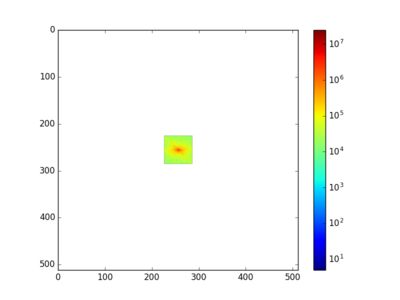
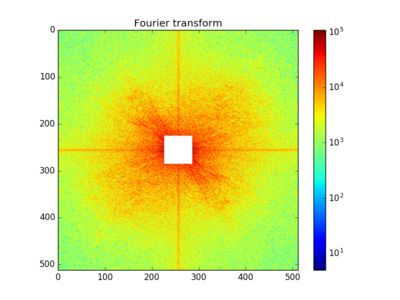
(4)对以上处理过的频谱图分别进行 反中心化、傅里叶反变换、取实部,得到 低通滤波 和 高通滤波 后的图像
![]()

C++分析
使用 CImg 和 FFTW库 对 lena图像进行傅里叶变换(源代码见文末),结果如下
![]()
源代码
以上所有代码均存储在我的Github仓库:
- Python Code: cggos/cgocv_app/cv_py
- C++ Code: cggos/cgocv_app/image_process/fftw_demos
参考资料
- 傅里叶分析之掐死教程
- Fourier Transforms (scipy.fftpack)
- Python下opencv使用笔记(十)(图像频域滤波与傅里叶变换)
- Fourier Transform (OpenCV-Python Tutorials)
- SIGNAL PROCESSING WITH NUMPY II - IMAGE FOURIER TRANSFORM : FFT & DFT
- 《数字图像处理与计算机视觉——Visual C++与MATLAB实现》
- 《积分变换》