Java8 - ArrayBlockingQueue源码

一、概述

ArrayBlockingQueue 是一个基于循环数组的有界阻塞队列，一旦创建了队列，那么其容量就不能再改变了，它不允许 null 值的插入。它是通过使用 ReentrantLock 来保证线程安全。

ArrayBlockingQueue 支持对生产者线程和消费者线程进行公平的调度，默认情况下是不保证公平性的。公平性通常会降低吞吐量，但是可以减少了可变性和避免了线程饥饿。

二、循环数组

PS：接触过循环数组这种数据结构的，可以直接跳过这一小节。

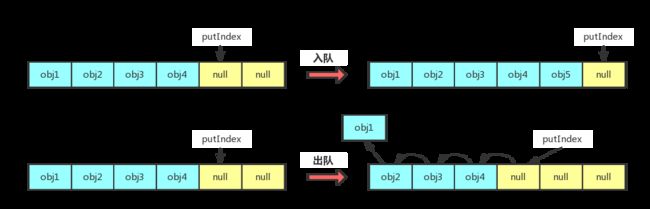
通常，队列的实现方式有数组和链表两种方式。对于数组这种实现方式来说，我们可以通过维护一个队尾指针，使得在入队的时候可以在O(1)的时间内完成；但是对于出队操作，在删除队头元素之后，必须将数组中的所有元素都往前移动一个位置，这个操作的复杂度达到了O(n)，效果并不是很好。如下图所示：

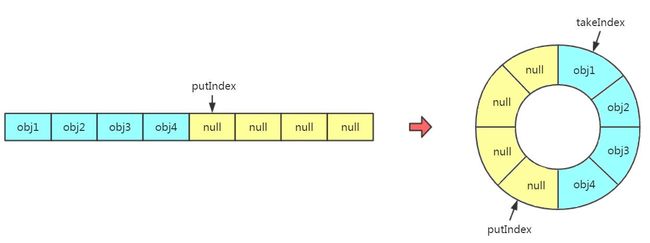
为了解决这个问题，我们可以使用另外一种逻辑结构来处理数组中各个位置之间的关系。假设现在我们有一个数组A[1…n]，我们可以把它想象成一个环型结构，即A[n]之后是A[1]，如下图所示：那么我们便可以使用两个指针，分别维护队头和队尾两个位置，使入队和出队操作都可以在O(1)的时间内完成，如下图所示。当然，这个环形结构只是逻辑上的结构，实际的物理结构还是一个普通的数据。

到此，我们对 ArrayBlockingQueue 使用的数据结构有了一定的了解，那么接下来我们就来看看它是怎么实现的。

三、属性

//队列的底层结构
final Object[] items;

//队头指针
int takeIndex;

//队尾指针
int putIndex;

//队列中的元素个数
int count;

final ReentrantLock lock;

//并发时的两种状态
private final Condition notEmpty;
private final Condition notFull;

四、方法

1、基本方法

下面的代码是入队和出队操作的实现，我们可以看到，putIndex 指向的是下一个插入的位置，而 takeIndex 指向的是队头元素的位置，如下图，通过这两个指针，我们就可以在 O(1) 的时间内完成入队和出队操作。

//入队
private void enqueue(E x) {
    // assert lock.getHoldCount() == 1;
    // assert items[putIndex] == null;
    final Object[] items = this.items;
    items[putIndex] = x;
    if (++putIndex == items.length)
        putIndex = 0;
    count++;
    //唤醒
    notEmpty.signal();
}

//出队
private E dequeue() {
    // assert lock.getHoldCount() == 1;
    // assert items[takeIndex] != null;
    final Object[] items = this.items;
    @SuppressWarnings("unchecked")
    E x = (E) items[takeIndex];
    items[takeIndex] = null;
    if (++takeIndex == items.length)
        takeIndex = 0;
    count--;
    if (itrs != null)
        itrs.elementDequeued();
    //唤醒
    notFull.signal();
    return x;
}

除了入队和出队操作之外，基本操作中还包含删除指定下标元素的操作，从代码中我们可以看到，删除指定下标的元素之后，必须把后面的元素都往前移动，所以这个操作的代价是非常高的。

//删除指定下标的元素
void removeAt(final int removeIndex) {
    // assert lock.getHoldCount() == 1;
    // assert items[removeIndex] != null;
    // assert removeIndex >= 0 && removeIndex < items.length;
    final Object[] items = this.items;
    if (removeIndex == takeIndex) {
        // removing front item; just advance
        items[takeIndex] = null;
        if (++takeIndex == items.length)
            takeIndex = 0;
        count--;
        if (itrs != null)
            itrs.elementDequeued();
    } else {
        // an "interior" remove

        // slide over all others up through putIndex.
        final int putIndex = this.putIndex;
        for (int i = removeIndex;;) {
            int next = i + 1;
            if (next == items.length)
                next = 0;
            if (next != putIndex) {
                items[i] = items[next];
                i = next;
            } else {
                items[i] = null;
                this.putIndex = i;
                break;
            }
        }
        count--;
        if (itrs != null)
            itrs.removedAt(removeIndex);
    }
    notFull.signal();
}

---

2、入队操作

ArrayBlockingQueue 提供了多种入队操作的实现来满足不同情况下的需求，入队操作有如下几种：

public boolean add(E e);
public void put(E e) throws InterruptedException;
public boolean offer(E e);
public boolean offer(E e, long timeout, TimeUnit unit) throws InterruptedException;

下面是几种入队操作的具体实现，从源码中我们可以发现，这几种入队操作都直接或间接地调用了enqueue方法，所以只要搞清楚了enqueue方法，就已经没有什么难点了。这几种入队操作的区别如下：

• add(E e)：入队成功返回true，入队失败抛出 IllegalStateException 异常。
• put(E e)：如果队列满了，会一直等待，直到成功入队。
• offer(E e)：入队成功返回true，入队失败返回false。
• offer(E e, long timeout, TimeUnit unit)：在指定的时间内一直尝试入队，入队成功返回true，超时返回false。

public boolean add(E e) {
    return super.add(e);
}

//super.add(e)
public boolean add(E e) {
    if (offer(e))
        return true;
    else
        throw new IllegalStateException("Queue full");
}

public boolean offer(E e) {
    checkNotNull(e);
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        if (count == items.length)
            return false;
        else {
            enqueue(e);
            return true;
        }
    } finally {
        lock.unlock();
    }
}

public void put(E e) throws InterruptedException {
    checkNotNull(e);
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    try {
        //如果队列满了，则进行等待并释放锁，等待入队操作来唤醒
        while (count == items.length)
            notFull.await();
        enqueue(e);
    } finally {
        lock.unlock();
    }
}

public boolean offer(E e, long timeout, TimeUnit unit) throws InterruptedException {

    checkNotNull(e);
    long nanos = unit.toNanos(timeout);
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    try {
        while (count == items.length) {
            if (nanos <= 0)
                return false;
            nanos = notFull.awaitNanos(nanos);
        }
        enqueue(e);
        return true;
    } finally {
        lock.unlock();
    }
}

---

3、出队操作

同时，ArrayBlockingQueue 也提供了多种出队操作的实现来满足不同情况下的需求，如下：

public E poll();
public E poll(long timeout, TimeUnit unit) throws InterruptedException;
public E take() throws InterruptedException;

下面是几种出队操作的具体实现，与入队操作类似，这几种出队操作都直接或间接地调用了dequeue方法，所以如果搞清楚了前面的dequeue方法，就已经没有什么难点了。这几种出队操作的区别如下：

• take()：如果队列为空，就一直等待，直到出队成功，并返回队头元素。
• poll()：如果队列不为空，则出队并返回队头元素，否则返回null。
• poll(long timeout, TimeUnit unit)：在指定的时间内一直尝试出队，出队成功返回队头元素，否则返回null。

public E poll() {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        return (count == 0) ? null : dequeue();
    } finally {
        lock.unlock();
    }
}

public E take() throws InterruptedException {
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    try {
        //如果队列为空，则进行等待并释放锁，等待出队操作来唤醒
        while (count == 0)
            notEmpty.await();
        return dequeue();
    } finally {
        lock.unlock();
    }
}

public E poll(long timeout, TimeUnit unit) throws InterruptedException {
    long nanos = unit.toNanos(timeout);
    final ReentrantLock lock = this.lock;
    lock.lockInterruptibly();
    try {
        while (count == 0) {
            if (nanos <= 0)
                return null;
            nanos = notEmpty.awaitNanos(nanos);
        }
        return dequeue();
    } finally {
        lock.unlock();
    }
}

---

4、其他方法

//只获取队头元素，不出队
public E peek() {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        //直接通过队头的下标获取队头元素
        return itemAt(takeIndex); // null when queue is empty
    } finally {
        lock.unlock();
    }
}

final E itemAt(int i) {
    return (E) items[i];
}

//获取队列中元素的个数
public int size() {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        return count;
    } finally {
        lock.unlock();
    }
}

//获取队列中剩余的存储空间
public int remainingCapacity() {
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        //数组长度 - 队列中元素个数
        return items.length - count;
    } finally {
        lock.unlock();
    }
}

//从队列中删除指定的对象
//删除操作会遍历整个数组，所以复杂度为O(n)
public boolean remove(Object o) {
    if (o == null) return false;
    final Object[] items = this.items;
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        if (count > 0) {
            final int putIndex = this.putIndex;
            int i = takeIndex;
            do {
                if (o.equals(items[i])) {
                    removeAt(i);
                    return true;
                }
                if (++i == items.length)
                    i = 0;
            } while (i != putIndex);
        }
        return false;
    } finally {
        lock.unlock();
    }
}

//判断队列中是否存在该元素
//该操作会遍历整个数组，所以复杂度为O(n)
public boolean contains(Object o) {
    if (o == null) return false;
    final Object[] items = this.items;
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        if (count > 0) {
            final int putIndex = this.putIndex;
            int i = takeIndex;
            do {
                if (o.equals(items[i]))
                    return true;
                if (++i == items.length)
                    i = 0;
            } while (i != putIndex);
        }
        return false;
    } finally {
        lock.unlock();
    }
}

//清空队列中的元素
//复杂度为O(n)
public void clear() {
    final Object[] items = this.items;
    final ReentrantLock lock = this.lock;
    lock.lock();
    try {
        int k = count;
        if (k > 0) {
            final int putIndex = this.putIndex;
            int i = takeIndex;
            do {
                items[i] = null;
                if (++i == items.length)
                    i = 0;
            } while (i != putIndex);
            takeIndex = putIndex;
            count = 0;
            if (itrs != null)
                itrs.queueIsEmpty();
            for (; k > 0 && lock.hasWaiters(notFull); k--)
                notFull.signal();
        }
    } finally {
        lock.unlock();
    }
}