Kaggle房价预测数据观察和处理入门学习

 https://www.kaggle.com/pmarcelino/comprehensive-data-exploration-with-python

 

COMPREHENSIVE DATA EXPLORATION WITH PYTHON

来自于Kaggle本房价预测比赛最高赞的kernel,介绍富有代码，简单生动，可以作为数据预处理的学习入门体会读物，并仿照代码来一通。

 

Pedro的大致过程如下：

1.    Understand the problem. 分析每个变量与输出房价的关系，它们的重要性，甚至靠自己的第六感和生活经验，这可以是自己熟悉这些数据，尤其在买房房价这种我们平时常常接触的事物上，生活经验和第六感往往对我们后面分析和避坑有巨大帮助。

Pedro列出需要关注的几个点：变量名 类型 含义 变量可用值   期望 重要性经验估 自己对变量的评论

 

最后作者猜想了如面积等具有重要因素可能的自变量。

 

 

2.    Univariable study. 直接对房价这个因变量进行讨论，类似第一步。

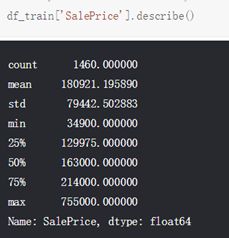
因变量理解，

 

直接将数据情况列出理解

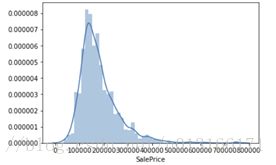
sns.distplot(df_train['SalePrice']);

并作出分布图

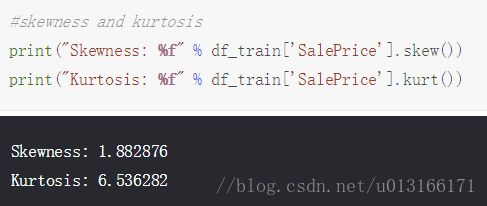
看出类似正太但有偏值

3.    Multivariate study. 分析自变量和因变量的关系

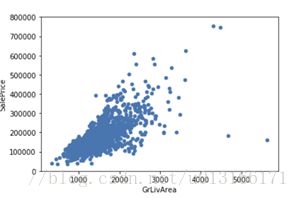
对于之前猜测有重要可能的变量，通过图可直接大概判断其中对应关系，需要做散点图。

var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));

尤其是线性关系。

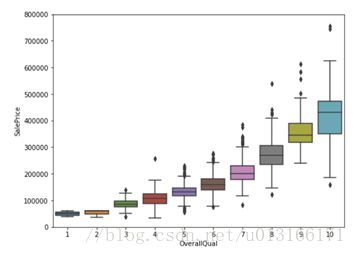
而对于离散分类自变量，也可以用类似方法进行分析。如作者猜测的有重要关系的整体质量。

var = 'OverallQual'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);

 

如果没时间对所有变量都细致分析，那至少把自己提取的重要先解决。而对于如地下室的面积这样存在大量0值而又和房价有线性关系的变量。要想办法用trick将其进行处理后使用。

 

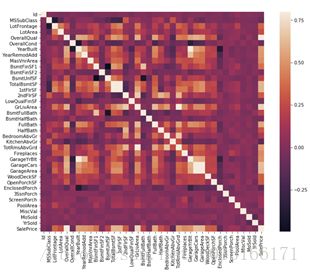
另外一个需要关注的就是自变量间的相关，以免使用相关性过高的变量造成重复使用等问题，通过热图可以快速把握。

#correlation matrix
corrmat = df_train.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);

加入数值看得更清晰，提取重要的因素：

#saleprice correlation matrix
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(df_train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size':10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()

 

 

 

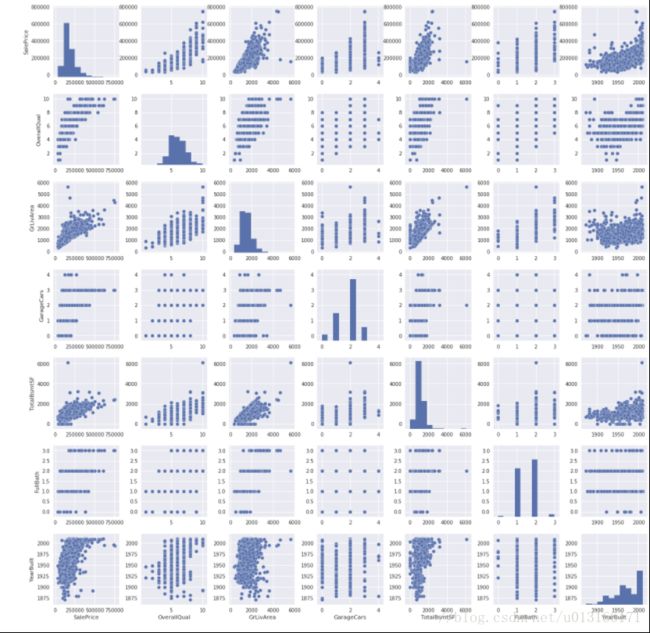
从而可以发现许多强相关变量，如'TotalBsmtSF' and'1stFloor'，在后边使用时只应该使用一个。还有一种更为清楚的相关图矩阵。

#scatterplot
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath','YearBuilt']
sns.pairplot(df_train[cols], size = 2.5)
plt.show();

 

 

 

4.    Basic cleaning. 让数据更适合符合处理的要求，包括缺失值异常值的处理，这里的处理Pedro处理比较简单些。

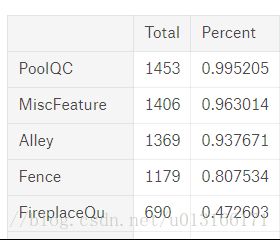
对于缺失值，需要观察有多少值缺失，丢失是否有规律，可以用方法弥补或者忽略，在数据量和数据有效性中找到平衡。

#missing data
total = df_train.isnull().sum().sort_values(ascending=False)
percent = (df_train.isnull().sum()/df_train.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)

 

 

 

Pedro直接考虑删除缺失超过15%时直接丢弃该自变量和缺失值存在且本身不重要的变量，极少量的丢失可以删除该样例。

 

异常值，作者使用将数据以期望和方差阀值来设定一个幅度的异常值幅度。并考虑去除无法解释的异常值以保证泛化能力和后面处理能力。

#standardizing data
saleprice_scaled = StandardScaler().fit_transform(df_train['SalePrice'][:,np.newaxis]);
low_range = saleprice_scaled[saleprice_scaled[:,0].argsort()][:10]
high_range= saleprice_scaled[saleprice_scaled[:,0].argsort()][-10:]
print('outer range (low) of the distribution:')
print(low_range)
print('\nouter range (high) of the distribution:')
print(high_range)

 

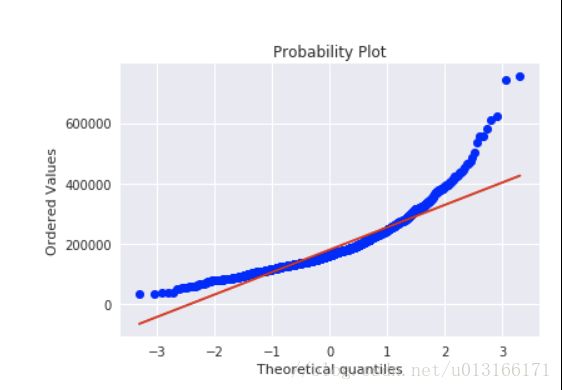
5.    Test assumptions. 最后一个非常重要，现有的统计知识与通用的计算方式常常需要数据本身符合理论的特定假设，否则不符合假设的数据难以使用特定方法求解。

根据Hair，应该测试这些变量：正态性  方差齐性“不太理解“  线性   没有相关错误。

 

 

sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

 

 

 

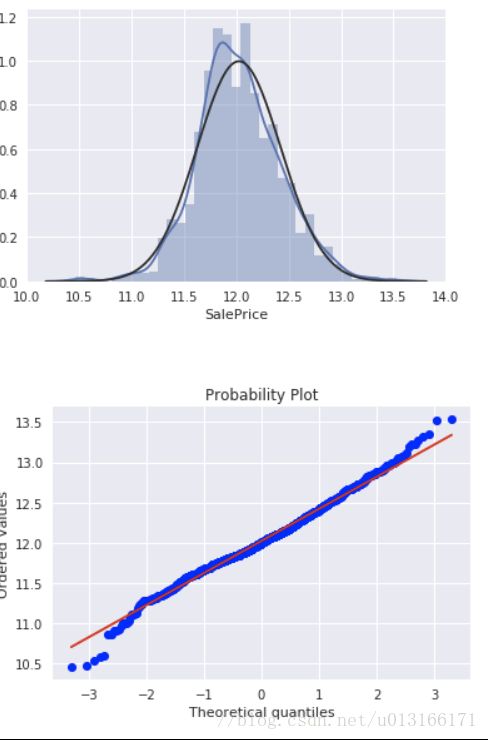
如销售价格就没有符合正态性,它显示'尖峰'，正偏斜，并不遵循对角线,可以使用log变化使其具备类似正态性。

 

df_train['SalePrice'] = np.log(df_train['SalePrice'])

 

 

sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)