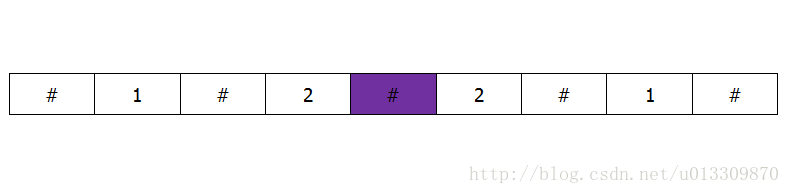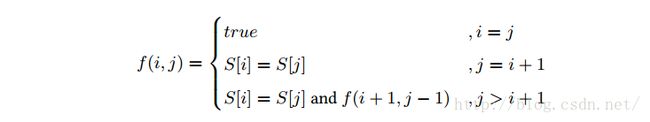笔试面试算法经典--最长回文子串
回文的定义
正读和反读都相同的字符序列为“回文”,如“abba”、“abccba”是“回文”,“abcde”和“ababab”则不是“回文”。字符串的最长回文子串,是指一个字符串中包含的最长的回文子串。例如“1212134”的最长回文子串是“12121”。下面给出了三种求最长子串的方法。
解法1(中心扩展法)
时间复杂度O(n^2),空间复杂度为O(1)。中心扩展法的思路是,遍历到数组的某一个元素时,以这个元素为中心,向两边进行扩展,如果两边的元素相同则继续扩展,否则停止扩展。如下图:当遍历到3时
![]()
但是中心扩展法有一个问题,如下图:
1,2,2,1是一个回文串,然而找不到对称中心,这样以一个元素为中心向两边扩展就不好用了,这里有一种比较方便的处理方式,就是对1,2,2,1进行填充,比如说用#进行填充如下:
如下图这样填充之后就又成了一个中心对称的回文串,因此对于一个串进行处理时,先进行扩充,这样可以使中心扩展时比较方便,不用对非中心对称的子串进行特殊处理。假设填充前的子串长度为 len 那么扩充或的长度为:2 * len+1,由这个关系也可以很方便的得到扩充前回文串的长度。
代码
public void palindrome(String str)
{
if(str==null||str.length()==0)
return ;
//如果str为null 或长度为0直接返回。
StringBuffer sb=new StringBuffer(str);
for(int i=0;i<str.length();i++)
{
sb.append("#");
sb.append(str.charAt(i));
}
//对给出的串进行填充。
sb.append("#");
char chs[]=sb.toString().toCharArray();
int max_len=0;
for(int i=0;i//遍历到位置i时,对i进行中心扩展
max_len=Math.max(subpalidromelen(chs,i), max_len);
//subpalidromelen(chs,i),以i为中心进行中心扩展,max_len 保存最长回文子串的长度。
}
System.out.println(max_len);
}
//中心扩展函数
public int subpalidromelen(char []chs,int i)
{
int len=0;
for(int k=0;k<=i&&k<(chs.length-i);k++)
{
if(chs[i-k]==chs[i+k])
{
len++;
}
else {
break;
}
}
return len-1;
//因为是填充之后的串,填充之前的回文子串值为len-1。
} 上面代码做两点说明:
①palindrome()对给出的字符串填充后进行遍历,对遍历的每一个元素调用中心扩展函数获得回文子串的值,并保存最长回文子串的值。
②subpalidromelen()中心扩展函数,返回回文子串的长度。
解法2(动态规划)
时间复杂度O(n^2),空间复杂度O(n^2),如果用f[i][j] 保存子串从i 到j是否是回文子串,那么在求f[i][j] 的时候如果j-i>=2时,如果 f[i][j] 为回文,那么f[i+1][j-1],也一定为回文。否则f[i][j]不为回文。如下图:
因此可得到动态规划的递归方程:
public void palindrome1(String str)
{
if(str==null||str.length()==0)
return ;
char chs[]=str.toCharArray();
int max_len=0;
boolean f[i][j]=new boolean[chs.length][chs.length];
for(int j=0;j<str.length();j++)
{
int i=0;
f[j][j]=true;
//一个元素肯定是回文串。
for(;i2||j>0&&f[i+1][j-1]));
//如果chs[j]==chs[i]当串的长度小于等于2时,肯定是回文子串,如 1,1,就是回文串。
//如果长度大于2时,则需要判断f[i+1][j-1]是不是回文。
if(f[i][j])
{
max_len=Math.max(max_len, j-i+1);
}
//max_len保存最大回文子串的长度。
}
}
System.out.println(max_len);
} 两点说明:
①当子串的长度为1时肯定为回文子串,对应上面的 f[j][j] = true 。当子串的长度为 2 且 里面的两个元素相同时,则也是回文子串。对应上面的 f[i][j]= chs[i]&&(j-i<2).
②当串的长度大于2时,如串为121时,要判断chs[j]==chs[i]&&f[i+1][j-1]),依赖子串。
Manacher
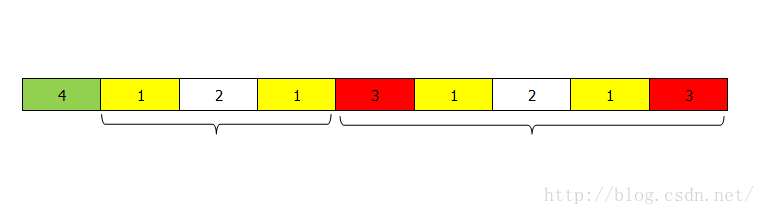
时间复杂度O(n),空间复杂度O(n)观察上面的中心扩展法,发现遍历到每一个元素的时候都要进行一次中心扩展,完全没有利用前面回文子串的信息,Manacher算法的核心思想,就是利用前面遍历的时候产生的回文子串,如下图:
上图中已经求出了红色部分3的回文子串,现在如何求3右边的1,2,1的回文子串呢,利用回文子串的对称性,如下图:

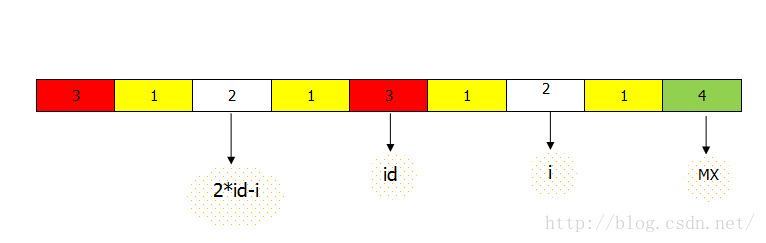
①2*id-i,id , i表示的是数组的下标,2*id-i 与 i 关于 id对称,如果用p[i],表示i位置的最长回文子串,则在上图的这种情况下p[i]=p[2*id-i],由于 p[2*id-i] 在3的左边已经求出来了,因此p[i]很快就可以得到,然而当要求右边2的最长回文的时候如下图:
②发现右边2的回文子串并不等于左边2的回文子串,而且比左边的要长,还有下面的这种情况:
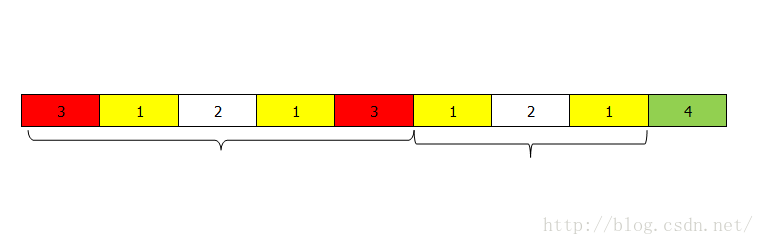
③左边2的回文怎么比右边2的回文长。
综合上面三种情况:其实可以的到下面的公式
由于manacher算法与上面中心扩展法有一样的问题,所以先向字符串中插入#,如下图:

在上面的基础上:
引入一个辅助变量MaxRight,表示当前访问到的所有回文子串,所能触及的最右一个字符的位置。另外还要记录下MaxRight对应的回文串的对称轴所在的位置,记为pos,它们的位置关系如下。
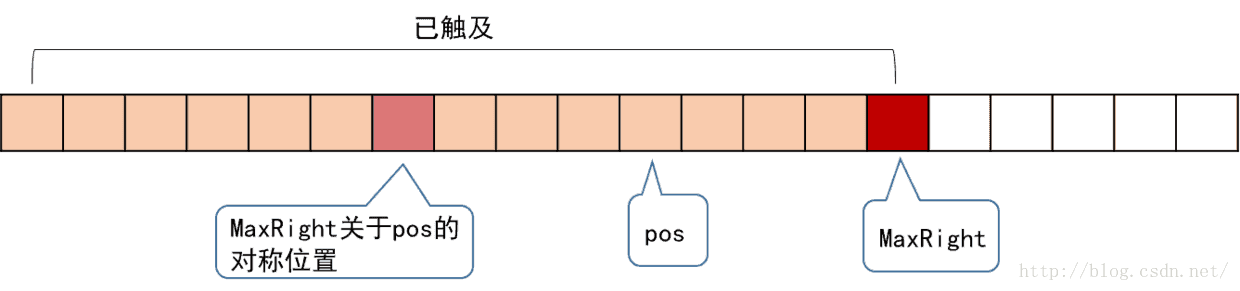
我们从左往右地访问字符串来求RL,假设当前访问到的位置为i,即要求RL[i],在对应上图,i必然是在po右边的(obviously)。但我们更关注的是,i是在MaxRight的左边还是右边。我们分情况来讨论。
1)当i在MaxRight的左边
情况1)可以用下图来刻画:
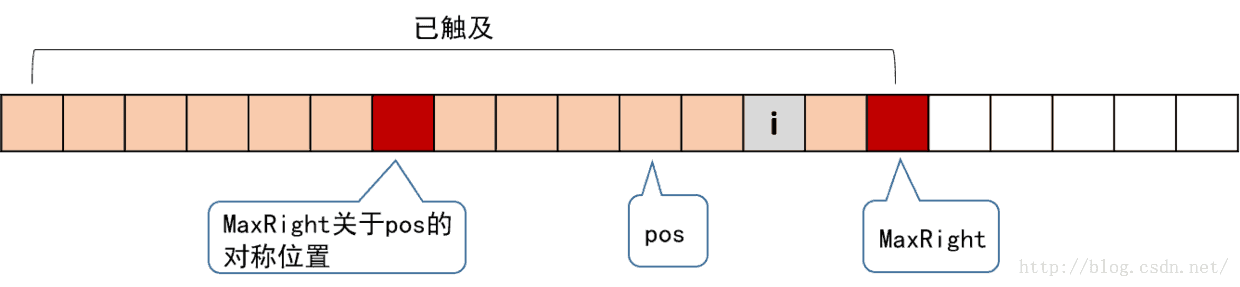
我们知道,图中两个红色块之间(包括红色块)的串是回文的;并且以i为对称轴的回文串,是与红色块间的回文串有所重叠的。我们找到i关于pos的对称位置j,这个j对应的RL[j]我们是已经算过的。根据回文串的对称性,以i为对称轴的回文串和以j为对称轴的回文串,有一部分是相同的。这里又有两种细分的情况。
以j为对称轴的回文串比较短,短到像下图这样。

这时我们知道RL[i]至少不会小于RL[j],并且已经知道了部分的以i为中心的回文串,于是可以令RL[i]=RL[j]。但是以i为对称轴的回文串可能实际上更长,因此我们试着以i为对称轴,继续往左右两边扩展,直到左右两边字符不同,或者到达边界。
遇到这种情况,说明以i为对称轴的回文串还没有任何一个部分被访问过,于是只能从i的左右两边开始尝试扩展了,当左右两边字符不同,或者到达字符串边界时停止。然后更新MaxRight和pos。
代码:
public void manacher(String str)
{
if(str==null||str.length()==0)
{
return;
}
int len=str.length();
StringBuffer sb=new StringBuffer(str);
for(int i=0;i"#");
sb.append(str.charAt(i));
}
sb.append("#");
//先往串中插入#后不用再区分两种情况了。
int id=0,i=0,mx=0;
int n=sb.length();
int p[]=new int[n];
int max_len=0;
char chs[]=sb.toString().toCharArray();
for(i=1;iif(mx>i)
p[i]=Math.min(p[2*id-i], mx-i);
//如果i在最大回文子串的中间,就可以利用上面的分析p[i]表示i的最长回文子串的长度
else {
p[i]=1;
//否则p[i]=1,
}
for(;(i-p[i]>=0&&i+p[i]//在上面的基础上进行扩展。
if(i+p[i]>mx)
{
mx=p[i]+i;
id=i;
}
//如果i+p[i]>mx,就更新mx。
max_len=Math.max(max_len, p[i]-1);
}
System.out.println(max_len);
} 参考文献:https://segmentfault.com/a/1190000003914228