哈希表
根据设定的哈希函数 H(key)和所选中的处理冲突的方法,将一组关键字映射到一个有限的、地址连续的地址集 (区间) 上,并以关键字在地址集中的“映像”作为相应记录在表中的存储位置,如此构造所得的查找表称之为“哈希表”。
构造哈希函数的方法
1. 直接定址法(数组)
哈希函数为关键字的线性函数H(key) = key 或者 H(key) = a*key + b
此法仅适合于:地址集合的大小 == 关键字集合的大小
2. 数字分析法
假设关键字集合中的每个关键字都是由 s 位数字组成 (u1, u2, …, us),分析关键字集中的全体, 并从中提取分布均匀的若干位或它们的组合作为地址。
此方法仅适合于:能预先估计出全体关键字的每一位上各种数字出现的频度。
3. 平方取中法
以关键字的平方值的中间几位作为存储地址。求“关键字的平方值”的目的是“扩大差别” ,同时平方值的中间各位又能受到整个关键字中各位的影响。
此方法适合于:关键字中的每一位都有某些数字重复出现频度很高的现象。
4. 折叠法
将关键字分割成若干部分,然后取它们的叠加和为哈希地址。有两种叠加处理的方法:移位叠加和间界叠加。
此方法适合于:关键字的数字位数特别多;
5. 除留余数法
设定哈希函数为:{H(key) = key % p | 其中,p≤m(表长)并且p 应为不大于 m 的素数或是不含 20 以下的质因子}
为什么要对 p 加限制?
例如:给定一组关键字为:12, 39, 18, 24, 33,21,若取 p=9, 则他们对应的哈希函数值将为:3, 3, 0, 6, 6, 3;
可见,若 p 中含质因子 3, 则所有含质因子 3 的关键字均映射到“3 的倍数”的地址上,从而增加了“冲突”的可能。
6. 随机数法
设定哈希函数为:H(key) = Random(key)其中,Random 为伪随机函数;
通常,此方法用于对长度不等的关键字构造哈希函数。
(如果关键字并不是数字, 则还需先对其进行数字化处理。)
实际造表时,采用何种构造哈希函数的方法取决于建表的关键字集合的情况(包括关键字的范围和形态),总的原则是使产生冲突的可能性降到尽可能地小(下面我们将以除留余数法构造哈希函数)。
处理冲突的方法
“处理冲突” 的实际含义是:为产生冲突的地址寻找下一个哈希地址。
1. 开放定址法
为产生冲突的地址 H(key) 求得一个地址序列:{ H0, H1, …, Hs|1≤ s≤m-1}
其中: H0 = H(key)
Hi = ( H(key) + di ) % m {i=1, 2, …, s}
对增量 di 有三种取法:
1) 线性探测再散列
di = c * i 最简单的情况 c=1
2) 平方探测再散列
di = 1^2, -1^2, 2^2, -2^2, …,
3) 随机探测再散列
di 是一组伪随机数列或者di=i×H2(key) (又称双散列函数探测)
注意:增量 di 应具有“完备性”,即:产生的 Hi 均不相同,且所产生的s(m-1)个 Hi 值能覆盖哈希表中所有地址。则要求:
※ 平方探测时的表长 m 必为形如 4j+3 的素数(如: 7, 11, 19, 23, … 等);
※ 随机探测时的 m 和 di 没有公因子。
2. 链地址法(又称拉链法)
将所有哈希地址相同的记录都链接在同一链表中(我们将采用的方法)。
哈希表的设计与实现
//哈希表设计
template
class HashTable
{
public:
typedef typename vector::size_type size_type;
public:
explicit HashTable(int tableSize = 101)
: theList(tableSize), currentSize(0) {}
~HashTable()
{
makeEmpty();
}
//判断元素x是否存在于哈希表中
bool contains(const HashedObj &x) const;
void makeEmpty();
bool insert(const HashedObj &x);
bool remove(const HashedObj &x);
private:
vector< list > theList;
size_type currentSize;
void rehash();
int myHash(const HashedObj &x) const;
}; 哈希函数
//如果关键字并不是数字, 则需先对其进行数字化处理
template
int hash(Type key)
{
return key;
}
template<>
int hash(const string &key)
{
int hashVal = 0;
for (size_t i = 0; i < key.length(); ++i)
{
hashVal = 37 * hashVal * key[i];
}
return hashVal;
}
//哈希函数
template
int HashTable::myHash(const HashedObj &x) const
{
//首先对key进行数字化处理
int hashVal = hash(x);
//计算哈希下标
hashVal = hashVal % theList.size();
if (hashVal < 0)
hashVal += theList.size();
return hashVal;
} 哈希表的插入
//插入
template
bool HashTable::insert(const HashedObj &x)
{
//首先找到应该插入的桶(链表)
list &whichList = theList[ myHash(x) ];
//哈希表中已经存在该值了
if (find(whichList.begin(), whichList.end(), x) != whichList.end())
return false;
//插入桶中
whichList.push_back(x);
//如果此时哈希表已经"满"了(所存储的元素个数 = 哈希表的槽数)
//装载因子 == 1, 为了获取更好的性能, 再哈希
if (++ currentSize > theList.size())
rehash();
return true;
} 再哈希
//判断是否是素数
bool is_prime(size_t n)
{
if (n == 1 || !n)
return 0;
for (size_t i = 2; i*i <= n; i++)
if (!(n%i))
return 0;
return 1;
}
//寻找下一个素数
size_t nextPrime(size_t n)
{
for (size_t i = n; ; ++i)
{
if (is_prime(i))
return i;
}
return -1;
}//再哈希
template
void HashTable::rehash()
{
vector< list > oldList = theList;
//以一个大于原表两倍的第一个素数重新设定哈希桶数
theList.resize( nextPrime(2*theList.size()) );
//将原表清空
for (typename vector< list >::iterator iter = theList.begin();
iter != theList.end();
++ iter)
iter -> clear();
//将原表的数据插入到新表中
for (size_type i = 0; i < oldList.size(); ++i)
{
typename list::iterator iter = oldList[i].begin();
while (iter != oldList[i].end())
{
insert(*iter ++);
}
}
} 哈希表的查找
查找过程和造表过程一致。假设采用开放定址处理冲突,则查找过程为:对于给定值 K, 计算哈希地址 i = H(K),若 r[i] = NULL 则查找不成功,若 r[i].key = K 则查找成功否则 “求下一地址 Hi” ,直至 r[Hi] = NULL (查找不成功)或r[Hi].key = K (查找成功) 为止。
而我们采用比较简单的链地址法(也称拉链法的查找实现):
//查找:判断哈希表中是否存在该元素
template
bool HashTable::contains(const HashedObj &x) const
{
const list &whichList = theList[ myHash(x) ];
if (find(whichList.begin(), whichList.end(), x) != whichList.end())
return true;
return false;
} 哈希表查找的分析:
从查找过程得知,哈希表查找的平均查找长度实际上并不等于零。决定哈希表查找的ASL的因素
1)选用的哈希函数;
2)选用的处理冲突的方法;
3)哈希表饱和的程度,装载因子 α=n/m 值的大小(n:记录数,m:表的长度)
一般情况下,可以认为选用的哈希函数是“均匀”的,则在讨论ASL时,可以不考虑它的因素。
因此,哈希表的ASL是处理冲突方法和装载因子的函数。可以证明,查找成功时有下列结果
线性探测再散列:
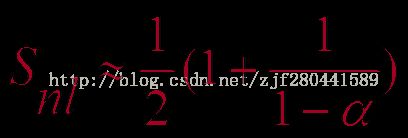
随机探测再散列:
链地址法
从以上结果可见:哈希表的平均查找长度是装载因子的函数,而不是 n 的函数;这说明,用哈希表构造查找表时,可以选择一个适当的装填因子,使得平均查找长度限定在某个范围内(这是哈希表所特有的特点).
哈希表的删除操作
//删除
template
bool HashTable::remove(const HashedObj &x)
{
list &whichList = theList[ myHash(x) ];
typename list::iterator iter = find(whichList.begin(), whichList.end(), x);
//没有找到该元素
if (iter == whichList.end())
return false;
whichList.erase(iter);
-- currentSize;
return true;
} 清空哈希表
//清空哈希表
template
void HashTable::makeEmpty()
{
for (typename vector< list >::iterator iter = theList.begin();
iter != theList.end();
++ iter)
{
iter -> clear();
}
} 附1-测试代码
int main()
{
HashTable iTable;
// 1 2 3 4 5 6 7 8 9 10
for (int i = 0; i < 10; ++i)
iTable.insert(i+1);
for (int i = 0; i < 10; ++i)
if (iTable.contains(i+1))
cout << i << ": contains..." << endl;
else
cout << i << ": not contains" << endl;
cout << endl;
//1 2
for (int i = 0; i < 10; ++i)
iTable.remove(i+3);
for (int i = 0; i < 10; ++i)
if (iTable.contains(i))
cout << i << ": contains..." << endl;
else
cout << i << ": not contains" << endl;
cout << endl;
// 6 8
iTable.makeEmpty();
iTable.insert(6);
iTable.insert(8);
for (int i = 0; i < 10; ++i)
if (iTable.contains(i))
cout << i << ": contains..." << endl;
else
cout << i << ": not contains" << endl;
return 0;
} 附2-各类算法复杂度的比较


