LeetCode刷题——第二周（动态规划系列）

887. 鸡蛋掉落

题目表述：题目表述
太难了，理解过程，掌握思想即可。数学思维强烈。动态规划列表的行表示楼层数列表示蛋蛋的数量。
当K = 2时，即蛋的数量为2。

蛋\层	1	2	3	4	5	6
1	max(dp(0,0), dp(1,5))	max(dp(0,1), dp(1,4))	max(dp(0,2), dp(1,3))	max(dp(0,3), dp(1,2))	max(dp(0,4), dp(1,1))	max(dp(0,5), dp(1,0))
2	max(dp(1,0), dp(2,5))	max(dp(1,1), dp(2,4))	max(dp(1,2),dp(2,3))	max(dp(1,3),dp(dp(2,2)))	max(dp(1,4),dp(2,1))	max(dp(1,5),dp(2,0))

其中dp(K,N)表示剩余的完整蛋蛋的数量为K，待测试的楼层数为N。在鸡蛋数量多于1个时，总是可以归结为这两种情况：
1.在测试的第i层上测试的蛋蛋碎了，则手中的蛋蛋数量少了一个即K-1,而待测试的楼层为第i层往下的楼层数即为i-1;
2.在测试的第i层上测试的蛋蛋没碎了，则手中的蛋蛋数量不变即K,而待测试的楼层数为第i层往上的层数即为N-i；
在不确定F的值时要确定最小的测试步数，必须要取每一种情况的最大值，即max(dp(K-1, i-1), dp(K, N-i))。
为了求出最小的测试步数，就只能取全表的最小值。即$$min(max(dp(0,0),dp(1,5)),max(dp(0,1),dp(1,4)),max(dp(0,2),dp(1,3)),max(dp(0,3),dp(1,2)),max(dp(0,4),dp(1,1)),max(dp(0,5),dp(1,0)),max(dp(1,0),dp(2,5))|max(dp(1,1),dp(2,4)),max(dp(1,2),dp(2,3)),max(dp(1,3),dp(dp(2,2))),max(dp(1,4),dp(2,1)),max(dp(1,5),dp(2,0)))$$
太抽象了，之前的动态规划列表都是可以计算出数值的，但是这个的结果却还是依赖动态规划方程。
最终的状态转移方程如下：
$dp(K,N)=\underset{X=1...N}{\min }(max(dp(K-1,X-1),dp(K,N-X)))+1$
实现优化：
将X作为连续自变量可以得到dp(K,N)的关于X的函数如下所示：

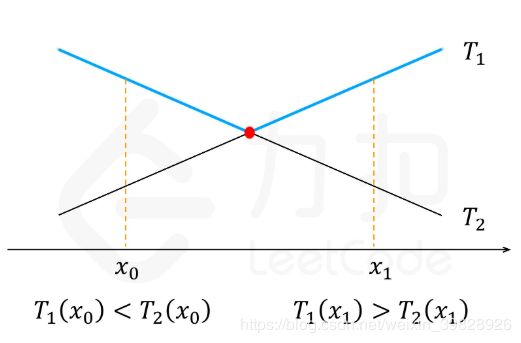
所以实现min的优化办法就是二分法，伪代码如下：

lower = 1, higher = N;
while(lower < higher){
	mid = (lower + higher)/2;
	if dp(K-1,mid-1) < dp(K, N - mid) lower 右移动;
	else if(dp(K-1,mid-1) > dp(K, N - mid)) higher 左移动;
}

代码实现如下：

class Solution {
public:
    int superEggDrop(int K, int N) {
        return dp(K, N);
    }

private:
unordered_map<int, int> memory;
    int dp(int K, int N)
    {
        if(K == 1){
            return N;
        }
        if(N == 0){
            return 0;
        }
        int low = 1, high = N;
        if(memory.find(100*N + K) == memory.end()){
        //while 的作用就是求min的实现
            while(low + 1  < high){
                int mid = (low + high) >> 1;
                int down = dp(K, N - mid);
                int raise = dp(K-1, mid - 1);
                if(down < raise){
                    high = mid;
                }else if(down > raise){
                    low = mid;
                }else{
                    low = high = mid;
                }
            }
            memory[100*N + K] = min(max(dp(K, N - low), dp(K-1, low - 1)), max(dp(K, N - high), dp(K - 1, high - 1))) + 1;
        }
        return memory[100*N + K];
    }
};

这道题有太多值得体会的地方：
1.数学思维–抽象动态规划列表
2.复杂状态转移方程的生成
2.复杂状态转移方程的优化与实现

354. 俄罗斯套娃信封问题

题目描述： 题目描述
这是一个最长上升子序列问题的升级。可以这样理解：envelopes的第一维数组即envelopes[0…N][0]从小到大排序后再求envelopes[0…N][1]的最长上升子序列.
最长上述子序列问题的求解思路见第一周总结ID300
实现相对简单，需要介绍lower_bound函数的功能：

ForwardIt lower_bound( ForwardIt first, ForwardIt last, const T& value );
ForwardIt lower_bound( ForwardIt first, ForwardIt last, const T& value, Compare comp );
返回指向范围 [first, last) 中首个不小于（即大于或等于） value 的元素的迭代器，或若找不到这种元素则返回 last 。
范围 [first, last) 必须已相对于表达式 element < value 或 comp(element, value) 划分，即所有令该表达式为 true 的元素必须前趋所有令该表达式为 false 的元素。完全排序的范围满足此判别标准。

实现如下：

   int maxEnvelopes(vector<vector<int>>& envelopes) {
        if(envelopes.size() == 0){
            return 0;
        }
        if(envelopes.size() == 1){
            return 1;
        }
        vector<int> dp;

        sort(envelopes.begin(), envelopes.end(),[](auto & a, auto &b){
            return a[0] < b[0] || (a[0] == b[0] && a[1] > b[1]);
        });

        for(auto &en : envelopes){
            int idx = lower_bound(dp.begin(), dp.end(), en[1]) - dp.begin();
            if(idx >= dp.size()){
                dp.emplace_back(en[1]);
            }else{
                dp[idx] = en[1];  //贪心的思想：
            }
        }

        return dp.size();
    }

152. 乘积最大子数组

问题描述：问题描述
对[2,3,-2,4,-1]做动态规划表如下,行为选择的当前元素，列为元素的下标。

	2	3	-2	4	-1
0	2
1		6
2			-12\6
3				-48\24
3					-24\48

最终结果为48。
找出状态转移方程
由于负数×负数也有可能是最大值，所以，dp[i]（以下标i结尾的最大乘积）所有可能的获得途径有：

1. $max(dp[i-1{]}_{max}\ast num[i],dp[i-1{]}_{min}\ast num[i],num[i])$
   所以每一个dp[i]都需要求出max和min，故状态转移方程如下：
   $dp[i{]}_{max}=max(dp[i-1{]}_{max}\ast num[i],dp[i-1{]}_{min}\ast num[i],num[i])$
   $dp[i{]}_{min}=min(dp[i-1{]}_{max}\ast num[i],dp[i-1{]}_{min}\ast num[i],num[i])$
   最后取最大值即可。
   优化空间
   显然，dp[i]的获得至于dp[i-1]有关，所以，可以使用简单变量代替即可。
   代码实现

   int maxProduct(vector<int>& nums) {
        int length = nums.size();
        if(length == 0){
            return 0;
        }

        int max_ele = nums[0];
        int min_ele = nums[0];
        int ans = max_ele;
        for(int i = 1; i < length; ++i){
            int tmp_max_ele = max(max(max_ele*nums[i], min_ele*nums[i]),nums[i]);  //code 1
            int tmp_min_ele = min(min(max_ele*nums[i], min_ele*nums[i]),nums[i]);  //code 2
            max_ele = tmp_max_ele;
            min_ele = tmp_min_ele;
            ans = max(max_ele, ans);
        }

        return ans;
    }

实现这块值得说的就是==为什么要使用tmp_max_ele 接收 max(max(max_elenums[i], min_elenums[i]),nums[i]);的值，而不是直接max_ele = max(max(max_elenums[i], min_elenums[i]),nums[i]);==因为code 2需要max_ele保持不变。

198. 打家劫舍

问题描述：问题

动态规划表
示例[1,2,3,1]，行表示元素值，列表示对应元素下标

	1	2	3	1
0	1
1		2
2			4
3				4

最大值为4

状态转移方程
$dp[i]=max(dp[i-2]+num[i],dp[i-1])$

空间优化
dp[i]的值只与dp[i-2]和dp[i-1]有关，可以使用两个简单变量替代数组。

代码实现

    int rob(vector<int>& nums) {
        int length = nums.size();
        if(length == 0)
            return 0;
        if(length == 1)
            return nums[0];

        int first = nums[0], second = max(nums[1],nums[0]);

        for(int i = 2; i < length; ++i){
            first = max(first+nums[i], second);
            //整型变量的两值交换办法
            first ^= second;  
            second ^= first;  
            first ^= second;  
        }
        return second;
    }

213. 打家劫舍 II

问题描述：问题
问题分析：不论房子多少都可以分两种情况，一是劫取第一个房子不劫取最后一个，二是劫取最后一个不劫取第一个房子。
然后在取两个情况的最大值。显然这一上一个问题的变形。
状态转移方程
$dp[i]=max(dp[i-2]+num[i],dp[i-1])$
代码实现

    int rob(vector<int>& nums) {

        int length = nums.size();

        if(length == 0){
            return 0;
        }
        if(length == 1){
            return nums[0];
        }
        if(length == 2){
            return max(nums[1],nums[0]);
        }

        int first = nums[0], second = max(nums[0],nums[1]);
//劫取第一个房子不劫取最后一个
        for(int i = 2; i < length-1; ++i){
            first = max(first+nums[i], second);
            first ^= second;
            second ^= first;
            first ^= second;
        }

        int ans = second;

        first = nums[1];
        second = max(nums[2],nums[1]);
   //劫取最后一个不劫取第一个房子
        for(int i = 3; i < length; ++i){
            first = max(first+nums[i], second);
            first ^= second;
            second ^= first;
            first ^= second;           
        }

        return ans > second? ans : second;
    }