希尔伯特黄变换(Hilbert-Huang)原理、HHT求时频谱、边际谱，及MATLAB（2018rb）实现

希尔伯特黄变换(Hilbert-Huang)包括两部分工作，分别是经验模态分解（EMD）和希尔伯特变换（HT）。

 

经验模态分解：

1. 找到信号x(t)的极大值和极小值，通过三次样条拟合得到上、下包络线，计算其均值得m1(t).
2. 得到第一个分量 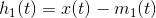  , 检擦其是否满足模态分量的条件： ①   得极大值点与过0点数量相差不超过1个；②  的上、下包络线均值恒为0。如不满足，重复操作1、2直至得到满足模态函数(IMF)条件的模态分量 .
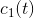3. 原始信号减去第一个模态分量，得到信号 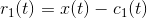 , 将  当成新的“原始信号”，重复以上操作，直至筛选条件 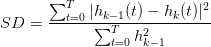             小于预设值时，经验模态分解结束。这样原始信号便分成若干经验模态分量和一个残余信号：   

 

希尔伯特变换：

对每个IMF ci(t)求其Hilbert变换： ; 根据和

可以求得相应IMF的瞬时频率和瞬时幅值，可将原始信号表示成      ,在经过n次EMD分解后，残余信号为常熟或单调函数，对信号提取没有实质影响，故舍去。

 

方法缺陷：

信号的端点不可能同时处于极大值或极小值，因此，上、下包络在数据序列两端会发散，且这种发散会随着运算的进行而逐渐向内，从而使得整个数据序列受到影响。EMD分解存在的端点效应，目前有端点镜像方法、多项式拟合法、极值延拓法、平行延拓法等进行改善。

 

MATLAB(2018rb版本)实现和探讨

clc
clear


%% 输入数据
fs = 1000;   % 取样频率设置为1000；对应ts的间隔为0.001；
ts = 0:0.001:0.3;
x = cos(2*pi*20*ts) + 2*cos(2*pi*200*ts);
N = length(x);

%% EMD和HT
figure()
% 画出每个IMF分量图
emd(x);
% 得到每个分量的数据
[imf,residual,info]=emd(x,'Interpolation','pchip','Display',0);

figure()

% 画出时频图
hht(imf,fs);
% 横轴表示时间、纵轴表示频率，颜色表示能量

[hs, f, t, imfinsf, imfinse] = hht(imf,fs);
% hs——信号的希尔伯特谱（Hilbert Spectrum ）   ###这里的出来的hs是乱序的
% f——信号的频率向量（Frequency vector of signal）
% t——信号的时间向量（Time vector of signal）
% imfinsf——每个imf的瞬时频率（instantaneous frequency of each imf）
% imfinse——每个imf的瞬时能量（instantaneous energy of each imf）

emd(x)得到的imf分量分布：

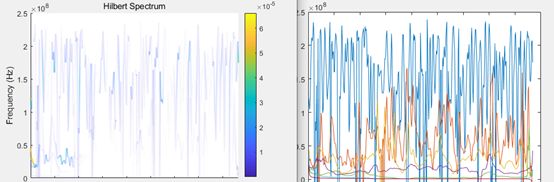
这是hht(x,fs)得到的频谱图：

 

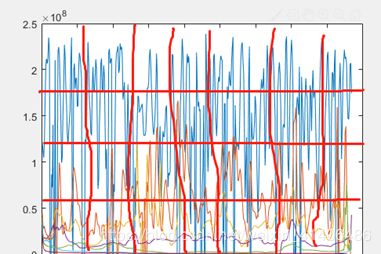
##其实对比时频谱图和imf分量图就可以发现，时频谱图是imf图加上能量分布而已，如下：

 

 

##边际谱

时频谱图已经出来，下面可根据边际谱求解公式求解边际谱。如下：

       这个公式是固定ω不变，对t积分。定积分在离散中可以近似分解为多个长方形的面积和。在离散信号中，H(ω,t)是时频谱矩阵H(ω,k)，长方形的长为第k个数据对应的H(ω,k),宽为时间间隔，即（采样频率的倒数），因此积分公式可改为如下公式：

因此，边际谱本来可以用一行代码搞定：

bjp = sum(hs,2)*1/fs

但问题来了，由自带函数HHT得到hs的数据顺序是错的。时频谱矩阵相当于把时频谱行方向用频率切割，列方向用时刻切割，得出多个小方块，每一个方块对应的频率用中心频率表示，对应的时刻则记录数据的时刻，小方块里的数据则表示该时刻，该频率的能量值（振幅的平方）。

 

hs是个稀疏矩阵，只记录非零的位置，和该位置对应的能量。但在这里，两者的顺序不同，hs记录的位置按以下方向记录：

 

然而对应的能量数据，是按得到的imfinse矩阵的顺序排列，两者不相匹配。因此，得到的hs矩阵是一个错误的时频谱矩阵，不能直接用来计算边际谱。

那么，接下来的工作只能根据得到的imf分量每一时刻的瞬时频率和瞬时能量来获得时频谱矩阵。

其实关键步骤是把每一个瞬时频率对应的小方格确定就可以了，然后把每一个小方格内的所有分量的能量累加即可：

时频矩阵大小和hs一样，最大频率为采样频率的一半。

[m,n] = size(hs);

中心频率向量确定：

spp_f = (1:m)/m*fs/2;

则每一个瞬时频率所在的小方格为:

k = round(imfinsf*m*2/fs);

然后把k<=0的剔除，再累加，就可以得到时频谱矩阵，然后计算得到边际谱。

 

详细代码可点此链接下载：

https://download.csdn.net/download/weixin_41406486/12239082