萌新改代码系列（一）--VINS+GPS

VINS与GPS组合

距离上次写博客过去了快一年了，这一年来我一直忙于与SLAM方向几乎没有关系的科研工作，说来惭愧，最终也没研究出个啥。最近得空，就把我之前开源的代码整理了一下，把与GPS的组合部分调好，并且利用实测数据进行了测试，应该是没什么问题的，然后就又开源了，希望感兴趣的同学们帮着挑挑毛病，然后别忘了关注、点赞、评论，最好在github上给个***小星星***。

闲话少说，github代码地址：VINS-GPS

在这个代码基础上我把轮速计也加上了，等整理一下，就开源。

很多同学问我我这个算紧组合吗，当然不算，我利用的是GPS的定位结果，又不是原始观测值（载波相位、伪距）；但是又和VINS-Fusion的松组合有着明显的不同。如果要区分，借用滤波算法的名词，我觉得我的方法是闭环松组合，VINS-Fusion是开环松组合。

本篇博客主要就是介绍我代码里的一些改动，以及我的一些理解。

代码改动主要分为两个部分，分别为初始化部分的坐标系对齐，以及滑动窗口优化部分的GPS因子的构建，包括残差和雅克比的定义。主要的代码对应为两个文件Coosys.h 和 gps_factor.h。下面分别对其进行介绍。

坐标系对齐

我们都知道，VINS的初始化部分还是蛮复杂的，先SFM，然后和IMU预积分的值对齐，优化重力、尺度等一系列操作，最后得到的导航坐标系是一个水平系–即重力方向竖直向下。但是其航向与真实的地理坐标系（东北天/北东地）相差一个角度，并且尺度和重力因子也并不一定是准确的，因此，要想融合，第一步先要把坐标系统一到地理坐标系下。

针对不同的GPS频率，我的程序中有两种不同的坐标系对齐方式，最常见的GPS频率是1HZ的，VINS默认的一个滑动窗口为11帧图像，最多也就两个GPS点来参与坐标系对齐，因此，这个时候只能认为VINS自己的初始化得到的重力方向是准确的，坐标系转换参数减少成4个-即 航向角、二维的水平位移以及尺度因子。这部分的代码非常简单，参考程序中的Coosys.h文件下的getRTWC2函数。而对于高频的GPS数据，只要滑窗内的GPS数量达到3个，就可以进行空间坐标系的对齐了–即7个参数的估计，在这里我用的优化的方法进行参数求解，具体的代码参考Coosys.h剩余代码。值得注意的是旋转有三个自由度，但是代码中用四元数表示旋转，因此需要重新定义其参数的广义加法。

#ifndef VINS_C00SYS_H
#define VINS_C00SYS_H

#include 
#include 
#include 
#include 

using namespace std;
using namespace Eigen;

class myPoseLocalParameterization : public ceres::LocalParameterization
{
    virtual bool Plus(const double *x, const double *delta, double *x_plus_delta) const
    {
        Eigen::Map<const Eigen::Vector3d> _p(x+1);
        Eigen::Map<const Eigen::Quaterniond> _q(x+4);
        
        Eigen::Map<const Eigen::Vector3d> dp(delta+1);

        Eigen::Quaterniond dq = Utility::deltaQ(Eigen::Map<const Eigen::Vector3d>(delta + 4));

        Eigen::Map<Eigen::Vector3d> p(x_plus_delta + 1);
        Eigen::Map<Eigen::Quaterniond> q(x_plus_delta + 4);

        x_plus_delta[0]=x[0]+delta[0];
        p = _p + dp;
        q = (_q * dq).normalized();

        return true;
    };
    virtual bool ComputeJacobian(const double *x, double *jacobian) const
    {
        Eigen::Map<Eigen::Matrix<double, 8, 7, Eigen::RowMajor>> j(jacobian);

        j.topRows<7>().setIdentity();
        j.bottomRows<1>().setZero();

        return true;
    };
    virtual int GlobalSize() const { return 8; };
    virtual int LocalSize() const { return 7; };
};

class MyScalarCostFunctor {
public:
    MyScalarCostFunctor(Vector3d pw,Vector3d pc): pw_(pw), pc_(pc) {}
    template <typename T>
    bool operator()(const T* const par , T* residuals) const {

        Matrix<T, 3, 1>  pww,pcc;
        pww[0]=T(pw_[0]);
        pww[1]=T(pw_[1]);
        pww[2]=T(pw_[2]);
        pcc[0]=T(pc_[0]);
        pcc[1]=T(pc_[1]);
        pcc[2]=T(pc_[2]);
        T s=par[0];
        Matrix<T, 3, 1> tt(par[1],par[2],par[3]);
        Quaternion<T> qq(par[7],par[4],par[5],par[6]);
        Matrix<T, 3, 1> pre=pww-(s*(qq*pcc)+tt);
        residuals[0] = pre[0];
        residuals[1] = pre[1];
        residuals[2] = pre[2];
        return true;
    }

    static ceres::CostFunction* Create(const Vector3d pww, const Vector3d pcc){
        return (new ceres::AutoDiffCostFunction<MyScalarCostFunctor,3,8>(
                new MyScalarCostFunctor(pww,pcc)));
    }

private:
    Vector3d pw_;
    Vector3d pc_;
};

inline int getRTWC(const vector<Vector3d> &pws, const vector<Vector3d> &pcs, Matrix3d &RWC , Vector3d &TWC ,double &SWC ) {

    double par[8]={1,0,0,0,0,0,0,1};
    ceres::Problem problem;
    ceres::LossFunction* loss_function = new ceres::HuberLoss(1.0);
    
    ceres::LocalParameterization *local_parameterization = new myPoseLocalParameterization();
    problem.AddParameterBlock(par, 8, local_parameterization);

    for(size_t i=0;i<pws.size();i++)
    {
        ceres::CostFunction* cost_function=MyScalarCostFunctor::Create(pws[i],pcs[i]);
        problem.AddResidualBlock(cost_function, loss_function, par);
    }

    ceres::Solver::Options options;

    options.linear_solver_type = ceres::DENSE_SCHUR;
    options.num_threads = 8;
    options.trust_region_strategy_type = ceres::LEVENBERG_MARQUARDT;
    options.max_num_iterations=100;
    ceres::Solver::Summary summary;
    ceres::Solve(options, &problem, &summary);
    Quaterniond q(par[7],par[4],par[5],par[6]);
    RWC=q.toRotationMatrix();
    TWC[0]=par[1];
    TWC[1]=par[2];
    TWC[2]=par[3];
    SWC=par[0];
    
    double sum=0;
    int num=pws.size();

    for(size_t i=0;i<pws.size();i++)
    {
        Vector3d pww=SWC*(RWC*pcs[i])+TWC;
        Vector3d dis=pws[i]-pww;
        cout<<"********"<<dis.transpose()<<endl;
        double dd=sqrt(dis[0]*dis[0]+dis[1]*dis[1]+dis[2]*dis[2]);
        sum+=dd;
    }
    if(sum/num > 0.05)
        return 0;
    return 1;
}

inline int getRTWC2(const vector<Vector3d> &pws, const vector<Vector3d> &pcs, Matrix3d &RWC , Vector3d &TWC ,double &SWC ) 
{
    Vector2d pw0(pws[0][0],pws[0][1]);
    Vector2d pw1(pws[1][0],pws[1][1]);
    Vector2d pc0(pcs[0][0],pcs[0][1]);
    Vector2d pc1(pcs[1][0],pcs[1][1]);
    Vector2d vw=pw1-pw0;
    Vector2d vc=pc1-pc0;
    double yaw1=atan2(vw[1],vw[0]);
    double yaw2=atan2(vc[1],vc[0]);
    double yaw=yaw1-yaw2;
    double s=vw.norm()/vc.norm();
    Matrix2d R;
    R<<cos(yaw),-sin(yaw),
       sin(yaw), cos(yaw);
    Vector2d Pc0=R*pc0*s;
    Vector2d Pc1=R*pc1*s;
    Vector2d a=pw1-Pc1;
    Vector2d b=pw0-Pc0;
    cout<<"*****"<<a.transpose()<<endl;
    cout<<"*****"<<b.transpose()<<endl;
    
    SWC=s;
    TWC[0]=(a[0]+b[0])/2.0;
    TWC[1]=(a[1]+b[1])/2.0;
    TWC[2]=0.0;
    RWC<< cos(yaw),-sin(yaw),0.0,
          sin(yaw), cos(yaw),0.0,
          0.0        , 0.0  ,1.0;

    double sum=0;
    int num=pws.size();
    double kkk=0.0;
    for(size_t i=0;i<pws.size();i++)
    {
        Vector3d pww=SWC*(RWC*pcs[i])+TWC;
        Vector3d dis=pws[i]-pww;
        kkk+=dis[2];
        cout<<"********"<<dis.transpose()<<endl;
        double dd=sqrt(dis[0]*dis[0]+dis[1]*dis[1]);
        sum+=dd;
    }
    TWC[2]=kkk/num;
    if(sum/num > 0.05)
        return 0;
    return 1;
   
}
#endif

gps_factor

仿照 IMU_factor,写了gps_factor，一个因子最主要的部分其实是残差和雅克比，其实对于这种松组合的残差定义非常简单，唯一需要注意的是，GPS定位的坐标和IMU并不是严格在一起的，中间存在着杆臂（平移），当然我没有在线估计杆臂，我的程序认为杆臂是一个准确的值。

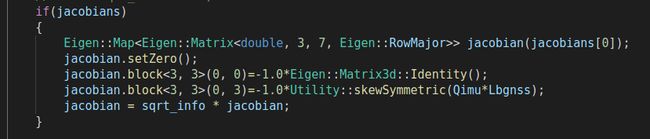
相应的雅克比矩阵可以手写，也很简单，也可以用ceres的自动求导，我的代码两种方法都有实现，但是为了保证和vins自己的各个factor的一致性，程序最后选择了手写雅克比。

其他改动

去掉了边缘化部分，我觉得GPS如果不参与边缘化可能会导致系统的不一致（可能也不对），但是GPS参与边缘化确实比较麻烦，鉴于我当前还有其他科研任务，索性直接删了。

double2vector函数则是不再每次固定优化起点了（表述可能有点问题，能看懂的自然懂），但是刚才大佬告诉我，如果GPS缺失，会引发较大的问题，后面我会思考看这里有没有什么比较好的处理方法。

本着越省事越好的原则，我粗略改了个VINS+GPS的代码，并不完善，还有很多问题需要解决，只是希望能对大家有所启发，帮助。

另外，我的代码验证数据是我们自己采集的，暂时并不方便公布出来，当然后面可能会发布，敬请期待。

小星星 走起来 技术网红之路还得靠大家了，笔芯