推荐系统快速开发--豆瓣电影推荐系统的快速实战开发(二)

在我的上一篇博客中我简单解释了如何快速开发推荐系统的一些步骤,比如前期的数据分析,数据清洗过程,和后期的如何构建一个用户和物品的评分矩阵,如何利用计算皮尔森相关系数来寻找最相似的电影,这些过程和步骤可以让大家对推荐系统开发有一个初步的认识，在本文中我将对上一篇博客中的步骤和方法进一步细化,让大家能更详细的了解其中的一些细节。先来介绍一下基于用户的系统过滤过滤和基于物品协同过滤的一些差异。

基于用户协同过滤

                        

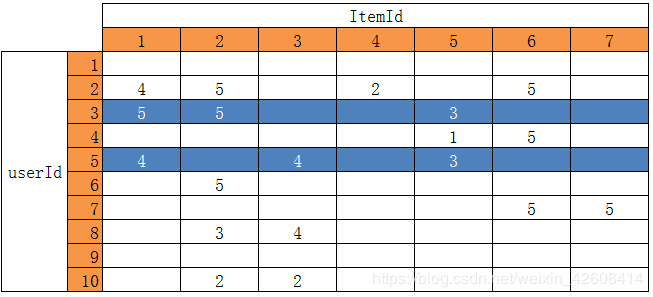
如果计算userId为3和5的两位用户之间的相似度,就是这计算两个用户的向量在多维空间中的距离

u3=[5,5,0,0,3,0,0],     u5=[4,0,4,0,3,0,0]

Similarity(u3,u5)=distance(u3,u5)

计算距离(distance)的公式包含欧氏距离、余弦距离,曼哈顿距离等多种,这里不一一展开说明，其中欧氏和余弦较为常用。

基于物品的协同过滤

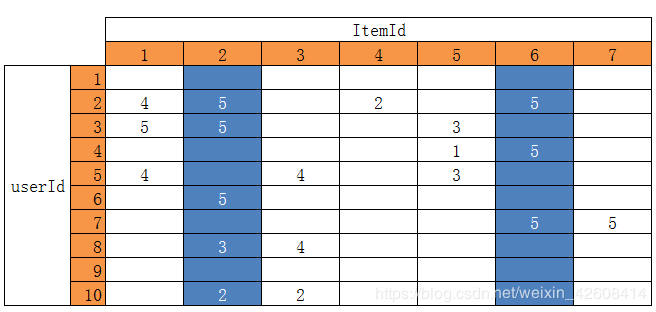
如果计算itemId为2和6的两个物品之间的相似度,就是计算这两个物品的向量在多维空间中的距离

I2=[0,5,5,0,0,5,0,3,0,2]   I6=[0,5,0,5,0,0,5,0,0,0]

Similarity(I2,I6)=distance(I2,I6)

distance的计算和上面描述的一样。

目前的协同过滤推荐算法主要分为两大类:1.基于计算相似度的KNN算法。2.基于矩阵分解的SVD算法。先来看看KNN算法

使用KNN算法的协同过滤

KNN的意思就是寻找K个距离最近的邻居(k-Nearest Neighbor)，以上面的列子为例,假设要寻找与itemId为2的物品最相近的3个物品，那么就要将I2向量逐一与剩下的9个物品的向量分别计算他们之间的距离，从而找出其中距离最近的3个物品。

from sklearn.metrics.pairwise import euclidean_distances
import numpy as np
I2=np.array([[0,5,5,0,0,5,0,3,0,2]])
I1=np.array([[0,4,5,0,4,0,0,0,0,0]])
dist=euclidean_distances(I2,I1)
print('distance between I2 and I1:',dist)

       

接着计算物品I2与剩下所有物品的距离就可以得到

最后我就可以找到I2与I1，I4，I5距离最近,它们也就是与I2最相似物品.接下来言归正传，开始我们的推荐系统开发！

数据

我们的数据来自于豆瓣电影网的用户点评数据,你可以在这里下载,用户点评数据包含了3个表,movies,ratings, links,我们只会用到其中的两个表,movies和ratings,首先我们查看一下数据

import pandas as pd
import numpy as np
from scipy.sparse import csr_matrix
from sklearn.neighbors import NearestNeighbors
import matplotlib.pyplot as plt
%matplotlib inline

movies = pd.read_csv( './data/douban/movies.csv')
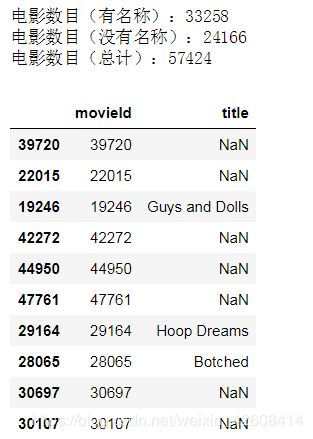
print('电影数目（有名称）：%d' % movies[~pd.isnull(movies.title)].shape[0])
print('电影数目（没有名称）：%d' % movies[pd.isnull(movies.title)].shape[0])
print('电影数目（总计）：%d' % movies.shape[0])
movies.sample(10)

ratings = pd.read_csv('./data/douban/ratings.csv')
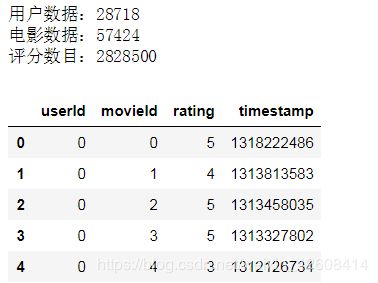
print('用户数据：%d' % ratings.userId.unique().shape[0])
print('电影数据：%d' % ratings.movieId.unique().shape[0])
print('评分数目：%d' % ratings.shape[0])
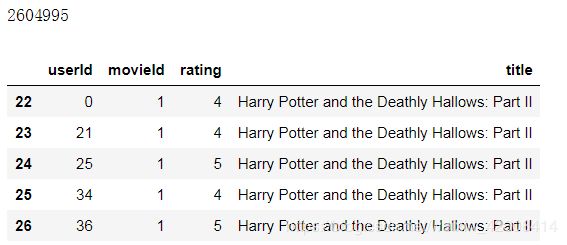
ratings.head()

 

 由于评分数据较多,我们将所有的数据都喂给我们的推荐算法，这样会导致内存溢出,会出现"内存错误"的问题，因此我们只要关注公众关注度比较高的电影,也就是那些评价次数多和评分也高的电影,因为那些评价差和评价次数少的电影也没有必要去推荐。

为了找出哪些电影的公众关注度比较高，我们需要整合一下movies表和rating表

combine_movie_rating= pd.merge(ratings,movies,on='movieId')
combine_movie_rating=combine_movie_rating.drop(['timestamp'],axis = 1)
print(len(combine_movie_rating))
combine_movie_rating.head()

 我们发现有大量的电影名称title为空的记录,所以我们要先过滤掉这些没有电影title的记录

combine_movie_rating = combine_movie_rating.dropna(axis = 0 ,subset=['title'])
print(len(combine_movie_rating))
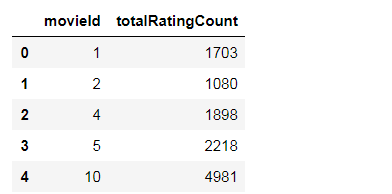
combine_movie_rating.head()

接下来我要统计一下每部电影总共的评价次数:

movie_rating_count=pd.DataFrame(combine_movie_rating.
                    groupby(['movieId'])['rating'].
                    count().
                    reset_index().
                    rename(columns={'rating':'totalRatingCount'})                   
                   )
movie_rating_count.head()

有了每部电影的总共评价次数以后,我们就可以想办法找出最受关注的电影,最流行的电影了，首先我们先查看一下总评价次数的分布情况

pd.set_option('display.float_format', lambda x: '%.3f' % x)
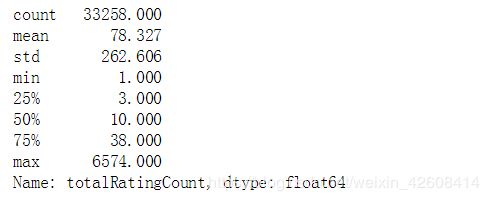
print(movie_rating_count['totalRatingCount'].describe())

我们可以看到电影总数是33258，其中有50%的电影评价次数小于10次，那说明还有另外50%的电影评价次数高于50%，还记得我上一篇博客中所使用的筛选流行电影的标准就是就是评价次数超过10次就是来源于这里。但是如果一部电影的评价次数只有10次左右的化，那还谈不上是部受关注的电影,所以它不应该被推荐，更不应该被"喂"给推荐算法参加计算。因为推荐算法在执行的时候会消耗大量系统资源,没有价值的数据不应该参与运算,否则会造成系统内存溢出,出现"内存错误"的问题。接下来我们还要查看分位数表中顶层的那10%的数据:

print(movie_rating_count['totalRatingCount'].quantile(np.arange(.9,1,.01)))

 我们可以看到有90%的电影评价次数少于158次，那也就是说还有另外10%的电影的评价次数超过了158次。还有9%的电影它们的评价次数超过了184次，还有8%的电影评价次数超过了211次，还有7%的电影评价次数超过了253次。我觉得如果一部电影的评价次数超过了158次的化，那应该是一部受关注的电影了把。那我们就暂时把158次作为识别流行电影的指标吧。(可能你有不同的想法,可以尝试其他指标)，目前电影总数有33258，那10%的话也应该有3325部电影，那我们就决定推荐这3325部电影。

#有10%的电影评价次数大于158次
popular_threshold=158
rating_popular_movies= rating_with_totalRatingCount.query('totalRatingCount>=@popular_threshold')
rating_popular_movies.head()

实现KNN算法

我们现在要构造一个用户对电影的评分矩阵,该矩阵每一行代表一个movie，每一列代表一个user，矩阵中的每一个值代表某位用户对某部电影的评分。如果用户对某部电影没有评价那就置为0。然后，我们将矩阵dataframe的值(rating)转换为稀疏矩阵，以便可以进行更有效的计算。

from scipy.sparse import csr_matrix
ratings_pivot = rating_popular_movies.pivot(index='movieId', columns='userId',values='rating').fillna(0)
ratings_pivot_sparse = csr_matrix(ratings_pivot.values)

然后我们使用sklearn.neighbors算法。并指定参数(metric='cosine', algorithm='brute')以便算法计算rating向量之间的余弦相似度。 最后，拟合我们的模型

model_nn_binary = NearestNeighbors(metric='cosine', algorithm='brute')
model_nn_binary.fit(ratings_pivot_sparse)

测试和推荐

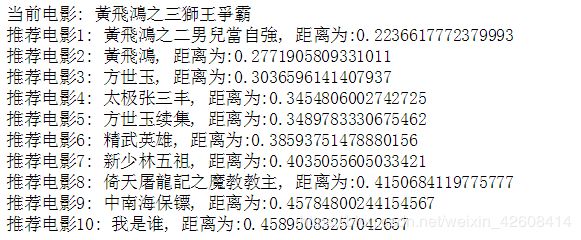
在这一步中，KNN算法开始计算当电影和其他所有电影的距离,并从中找出与当前电影距离最近的K个电影,我们还是那movieId=2550这部电影来做测试吧：

movieId=2550
distances, indices = model_nn_binary.kneighbors(ratings_pivot.query('movieId == 2550').values, n_neighbors = 11)

for i in range(0, len(distances.flatten())):
    likelymovieId=ratings_pivot.index[indices.flatten()[i]]
    if i == 0:
        print('当前电影:',movies[movies.movieId==movieId]['title'].values[0])
    else:
        print('推荐电影{0}: {1}, 距离为:{2}'.format(i, movies[movies.movieId==likelymovieId]['title'].values[0], 
                                                    distances.flatten()[i]))

看来效果还是非常不错的。

使用基于矩阵分解(SVD)算法的协同过滤 

奇异值分解(Singular Value Decomposition，以下简称SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。这里我们将通过sklearn的TruncatedSVD方法对原本巨大的用户对物品的评分矩阵进行分解和降维。将原来的矩阵的维度从(3329, 27895)降到(3329, 10)，我们只从原来矩阵中提取其中主要的10个特征,然后再此基础上再进行推荐,好了，废话少说,让我们撸起袖子干起来吧！

首先我们先生成一个用户-电影的评分矩阵，然后将其转换成一个稀疏矩阵(这样可以大大节省存储空间):

ratings_pivot2 = rating_popular_movies.pivot(index='userId', columns='movieId',values='rating').fillna(0)
ratings_pivot2_sparse = csr_matrix(ratings_pivot2.values)
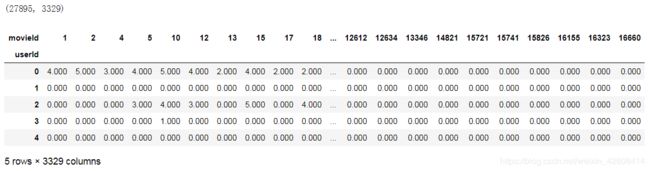
print(ratings_pivot2.shape)
ratings_pivot2.head()

该矩阵的维度是(27895,3329),矩阵的行代表userId,列代表movieId,然后我们再将它转置:

之所以要将矩阵转置,是因为我们做的是基于物品的协同过滤，我们必须要保留所有的movieId,然后从userId里面去抽取主要的特征,下面我们开始运用SVD算法，抽取主要特征,此处暂定抽取10个主要特征。

from sklearn.decomposition import TruncatedSVD
svd=TruncatedSVD(n_components=10,random_state=17)
matrix=svd.fit_transform(X)
matrix.shape

这时候我会看到矩阵原来的维度由(3329,27895)降到了(3329,10),我们保留了所有的movieId信息。接下来我们用经过降维的矩阵来计算一个相关系数矩阵:

import warnings
warnings.filterwarnings("ignore",category=RuntimeWarning)
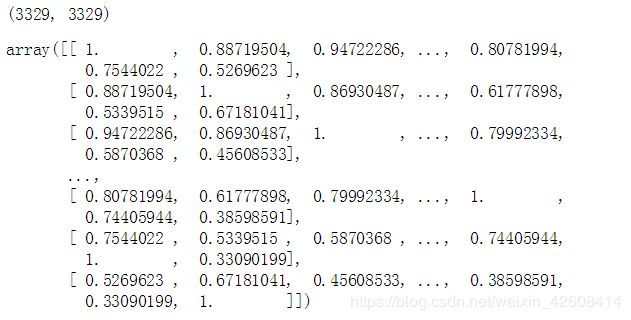
corr=np.corrcoef(matrix)
print(corr.shape)
corr

这个相关系统矩阵的维度为(3329,3329),其中的元素值表示任意两部电影它们的相关系数,相关系数取值范围为[-1,1],并且矩阵的主对角线元素值为1，表示每部电影自己与自己是完全相关的。

接下来我们还是找movieId为2550这部李连杰主要的黄飞鸿系列电影来测试一下推荐效果,首先我们要从相关系数矩阵中找出2250这部电影所在行的行向量,该行向量包含了2250这部电影与其他所有电影的相关系数,然后我们将该行向量进行降序排列,并抽取前11个相关系数最大的电影,并输出它们的movieId和相关系数值。

movieIds=ratings_pivot2.columns 
movieIds_list = list(movieIds)
movieId_index = movieIds_list.index(example_movieId)

movieId_vec=corr[movieId_index]
argsort_idx =np.argsort(-movieId_vec)[:11]
coff=movieId_vec[argsort_idx]
similar_movie_Ids=movieIds[argsort_idx]
print(similar_movie_Ids.values)
print('--------------------------------------------------------------')
print(coff)

最后我们将movieId转换成电影名称,看看推荐效果如何吧

for idx,mId in enumerate(similar_movie_Ids):
    name = movies[movies.movieId==mId]['title'].values[0]
    if idx==0:
        print('当前电影:',name)
    else:
         print('推荐电影{0}: {1}, 相关系数:{2}'.format(idx,name, coff[idx]))

 大家觉得这个推荐效果怎么样呢？

总结

今天我们学习了如何运用分位数统计的方法,来确定流行电影的阈值,科学的分析和清洗数据能提高推荐算法的执行效率,我们还学会了如何利用pivot方法来构造一个交叉表，以及运用sklearn的NearestNeighbors方法来计算电影之间的相似度(距离),并通过kneighbors方法来提取最相似的电影，最后我们使用TruncatedSVD方法从原来的超大矩阵中提取出10个主要特征，并通过这10个主要特征来计算它们的相关系数,并运用相关系数来推荐电影。

 

完整代码可以在此下载