LeetCode -- 查找问题
题目来源:
来源:力扣(LeetCode)
链接:https
文章目录
- 二分查找---神奇模板
- 一、二分查找
- 1.x 的平方根(Easy,题号:69)
- 2.寻找比目标字母大的最小字母(Easy)
- 3.有序数组中的单一元素(Meduim,题号:540)
- 4.第一个错误的版本(Easy,题号:278)
- 5.寻找旋转排序数组中的最小值(Medium,题号:153)
- 6. 在排序数组中查找元素的第一个和最后一个位置(Medium,题号:34)
- 7. 搜索旋转排序数组(Medium,题号:33)
- 8.Pow(x, n)求平方值(Medium,题号:50)
- 10.搜索二维矩阵(Medium,题号:74)
- 11.搜索旋转排序数组 II(Medium,题号:81)
- 12.寻找峰值(Medium,题号:81)
- 二、查找问题
- 1.两个数组的交集(Easy,题号:349)
- 2.两个数组的交集 II(Easy,题号:350)
- 3.有效的字母异位词(Easy,题号:242)
- 4.快乐数(Easy,题号:202)
- 5.单词规律(Easy,题号:290)
- 6.同构字符串(Easy,题号:205)
- 7.两数之和(Easy,题号:1)
- 8.三数之和(Medium,题号:15)
二分查找—神奇模板
链接:二分查找—神奇模板
一、二分查找
1.x 的平方根(Easy,题号:69)
第0次
题目链接:x 的平方根
题目描述:
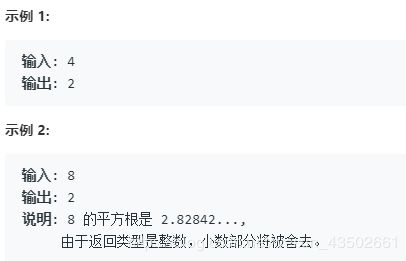
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
解题思路:利用二分查找,当x <= 1时,直接返回x,当x > 1时,令l = 1 , h = x,然后求l和h的中间值,然后令sqrt = x/m,比较sqrt和m的大小来调整l和h。回头再想想我的垃圾代码
代码:
参考代码(使用模板):
public int mySqrt(int x) {
if(x == 0)
return 0;
int l = 1;
int h = x;
while(l < h){
int m = (l + h + 1) >>> 1;
if(m > x/m)
h = m - 1;
else
l = m;
}
return l;
}
我的问题代码:
class Solution {
public int mySqrt(int x) {
if(x == 0 || x ==1)
return x;
int l = 1;
int h = x;
while(l <= h){
int m = l + (h-l)/2;
if(m*m == x){
return m;
}
else if(m*m < x){
l = m + 1;
}
else {
h = m - 1 ;
}
}
return h;
}
}
2.寻找比目标字母大的最小字母(Easy)
第1次
题目链接:寻找比目标字母大的最小字母
题目描述:
给定一个只包含小写字母的有序数组letters 和一个目标字母 target,寻找有序数组里面比目标字母大的最小字母。
数组里字母的顺序是循环的。举个例子,如果目标字母target = ‘z’ 并且有序数组为 letters = [‘a’, ‘b’],则答案返回 ‘a’。

解题思路:
代码:
参考代码:
public char nextGreatestLetter(char[] letters, char target) {
int n = letters.length;
int l = 0, h = n - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (letters[m] <= target) {
l = m + 1;
} else {
h = m - 1;
}
}
return l < n ? letters[l] : letters[0];
}
我的冗余代码:
public char nextGreatestLetter(char[] letters, char target) {
int l = 0;
int h = letters.length - 1;
int t = (int)target;
if(target >= letters[h]){
target = (char)((int)target - 26);
}
while(l <= h){
int mid = l + (h-l)/2;
if(letters[mid] == target){
while(mid < letters.length - 1 && letters[mid] == target){
mid++;
}
return letters[mid];
}
else if(letters[mid] > target){
h = mid -1;
}
else {
l = mid +1;
}
}
return letters[h+1];
}
3.有序数组中的单一元素(Meduim,题号:540)
第1次
题目链接:有序数组中的单一元素
题目描述:
给定一个只包含整数的有序数组,每个元素都会出现两次,唯有一个数只会出现一次,找出这个数。

解题思路:
我的思路:中规中矩地按照二分进行查找,根据中间数nums[m]与前一个数以及后一个数的比较,得出单个数的前后位置,考虑了所有情况;
参考思路:比较高级,保证中间数的左边和右边都为偶数个数,这时,只要中位数与左边相邻的数相等时,则单个数在中位数左边,中位数与右边相邻的数相等时,则单个数在中位数右边。
代码:
我的代码:
public int singleNonDuplicate(int[] nums) {
int l = 0;
int h = nums.length - 1;
while(l < h){
int m = l + (h-l)/2;
if(nums[m]!= nums[m-1] && nums[m] != nums[m+1])
return nums[m];
else if(nums[m] == nums[m-1] && m%2 == 0)
h = m;
else if(nums[m] == nums[m+1] && m%2 == 0)
l = m;
else if(nums[m] == nums[m-1] && m%2 == 1)
l = m +1;
else if(nums[m] == nums[m+1] && m%2 == 1)
h = m-1;
}
return nums[h];
}
参考代码:
public int singleNonDuplicate(int[] nums) {
int l = 0, h = nums.length - 1;
while (l < h) {
int m = l + (h - l) / 2;
if (m % 2 == 1) {
m--; // 保证 l/h/m 都在偶数位,使得查找区间大小一直都是奇数
}
if (nums[m] == nums[m + 1]) {
l = m + 2;
} else {
h = m;
}
}
return nums[l];
}
4.第一个错误的版本(Easy,题号:278)
第1次
题目链接:第一个错误的版本
题目描述:
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

解题思路:
代码:
我的垃圾代码:
public int firstBadVersion(int n) {
int l = 1;
int h = n;
while(l < h-1){
int m = l + (h-l)/2;
if(isBadVersion(m) == true)
h = m;
else if(isBadVersion(m) == false)
l = m;
}
if(isBadVersion(l) == true)
return l;
else
return h;
}
参考代码:
public int firstBadVersion(int n) {
int l = 1, h = n;
while (l < h) {
int mid = l + (h - l) / 2;
if (isBadVersion(mid)) {
h = mid;
} else {
l = mid + 1;
}
}
return l;
}
5.寻找旋转排序数组中的最小值(Medium,题号:153)
第2次
题目链接:寻找旋转排序数组中的最小值
题目描述:
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
请找出其中最小的元素。
你可以假设数组中不存在重复元素。

解题思路:
代码:
参考模板思路:
public int findMin(int[] nums) {
int l = 0;
int h = nums.length-1;
while(l < h){
int m = l + (h-l)/2;
if(nums[m] < nums[h])
h = m;
else
l = m + 1;
}
return nums[l];
}
6. 在排序数组中查找元素的第一个和最后一个位置(Medium,题号:34)
第1次
题目链接:在排序数组中查找元素的第一个和最后一个位置
代码:
class Solution {
public int[] searchRange(int[] nums, int target) {
if(nums.length == 0)
return new int[]{-1,-1};
int l = 0;
int h = nums.length-1;
while(l < h){
int m = l + (h-l)/2;
if(nums[m] < target){
l = m + 1;
}
else if(nums[m] > target){
h = m-1;
}
else {
l = m;
h = m;
}
}
while(l-1 >=0 && nums[l-1] == target){
l--;
}
while(h+1 < nums.length && nums[h+1] == target){
h++;
}
return nums[l] == target ? new int[]{l,h} : new int[]{-1,-1};
}
}
7. 搜索旋转排序数组(Medium,题号:33)
第1次
题目链接:搜索旋转排序数组
题目描述:
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。

解题思路:二分查找,通过判断中间数nums[m]与nums[h]的大小,来判定中间数的左边有序还是右边有序,判断要查找的数在不在有序的一半数组中,从而丢弃一半,实现二分查找。
代码:
class Solution {
public int search(int[] nums, int target) {
if(nums.length == 0)
return -1;
int l = 0;
int h = nums.length-1;
while(l < h){
int m = l + (h-l)/2;
if(nums[m] > nums[h]){ //数组左边有序
if(target >= nums[l] && target <= nums[m]){
h = m;
}
else {
l = m + 1;
}
}
else{ //数组右边有序
if(target > nums[m] && target <= nums[h]){
l = m+1;
}
else {
h = m;
}
}
}
return nums[l] == target ? l : -1;
}
}
8.Pow(x, n)求平方值(Medium,题号:50)
第0次
题目链接:Pow(x, n)求平方值
题目描述:
实现 pow(x, n) ,即计算 x 的 n 次幂函数。

解题思路:
通过折半计算的方式,减少了计算次数,降低了时间复杂度。
代码:
class Solution {
public double myPow(double x, int n) {
double res = 1.0;
for(int i = n; i != 0; i /= 2){
if(i % 2 != 0){
res *= x;
}
x *= x;
}
return n < 0 ? 1 / res : res;
}
}
10.搜索二维矩阵(Medium,题号:74)
第1次
题目链接:搜索二维矩阵
题目描述:
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

解题思路:使用两次二分法
代码:
public boolean searchMatrix(int[][] matrix, int target) {
if(matrix.length == 0 || matrix[0].length == 0)
return false;
int l = 0;
int h = matrix.length - 1;
int l1 = 0;
int h1 = matrix[0].length - 1;
while(l < h){
int m = (l + h) >>> 1;
if(matrix[m][h1] < target)
l = m + 1;
else
h = m;
}
while(l1 < h1){
int m = (l1 + h1) >>> 1;
if(matrix[l][m] < target)
l1 = m + 1;
else
h1 = m;
}
if(matrix[l][l1] == target)
return true;
else
return false;
}
11.搜索旋转排序数组 II(Medium,题号:81)
第1次
题目链接:搜索旋转排序数组 II
题目描述:
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,0,1,2,2,5,6] 可能变为 [2,5,6,0,0,1,2] )。
编写一个函数来判断给定的目标值是否存在于数组中。若存在返回 true,否则返回 false。

解题思路:先用两个while循环去掉与nums[l]和nums[h]相邻的重复元素,然后再分三种情况,一:中位数直接等于target,二:中位数左边有序(nums[m] >= nums[l],右边不一定有序),三:中位数右边有序(nums[m] < nums[l],左边不一定有序)。最后判断剩下的数nums[h](这里最后剩下的nums[h]一定的不变的,由于两个while循环,nums[l]可能已经越界)是否等于target。
代码:
public boolean search(int[] nums, int target) {
if(nums.length == 0)
return false;
int l = 0;
int h = nums.length - 1;
while(l < h){
while(l < h && nums[l] == nums[l+1]) l++;
while(l < h && nums[h] == nums[h-1]) h--;
int m = (l + h) >>> 1;
if(nums[m] == target){
l = m;
h = m;
}
else if(nums[m] >= nums[l]){
if(target > nums[m] || target < nums[l])
l = m + 1;
else
h = m;
}
else {
if(target > nums[m] && target <= nums[h])
l = m + 1;
else
h = m;
}
}
if(nums[h] == target)
return true;
else
return false;
}
12.寻找峰值(Medium,题号:81)
第1次
题目链接:寻找峰值
题目描述:
峰值元素是指其值大于左右相邻值的元素。
给定一个输入数组 nums,其中 nums[i] ≠ nums[i+1],找到峰值元素并返回其索引。
数组可能包含多个峰值,在这种情况下,返回任何一个峰值所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞。

解题思路:
O(N)解法:不符合要求,从l=0往后遍历,寻找一个下降点;
O(logN)解法:符合要求,二分法,若中位数nums[m]为即将下降的点,则中位数左边必然存在峰值点(若从nums[l]开始就一直递减,那么nums[l]算是峰值点,因为nums[-1] = 负无穷),否则,中位数右边一定存在峰值点(因为nums[h] = 负无穷,若nums[m]之后一直递增,那么至少最后一个元素算是峰值点)。
代码:
O(N)解法:
public int findPeakElement(int[] nums) {
if(nums.length == 0)
return 0;
int l = 0;
int h = nums.length - 1;
while(l < h){
if(nums[l] < nums[l+1]){
l++;
}
else
h = l;
}
return l;
}
O(logN)解法:
public int findPeakElement(int[] nums) { //优秀的代码
if(nums.length == 0)
return 0;
int l = 0;
int h = nums.length - 1;
while(l < h){
int m = (l + h) >>>1;
if(nums[m] > nums[m+1]){
h = m;
}
else {
l = m + 1;
}
}
return l;
}
二、查找问题
1.两个数组的交集(Easy,题号:349)
第1次
题目链接:两个数组的交集
题目描述:
给定两个数组,编写一个函数来计算它们的交集。

解题思路:
使用Set:使用两个Set集合,set和set1,先将数组nums1中的元素都放到set里,然后遍历nums2,看看set中是否包含nums2中的元素,包含则将该元素加到set1中,最后再遍历set1,将其中的元素都转化为数组。
代码:
使用Set:
public int[] intersection(int[] nums1, int[] nums2) {
Set<Integer> set = new HashSet<Integer>();
for(int i=0; i < nums1.length; i++){
set.add(nums1[i]);
}
Set<Integer> set1 = new HashSet<Integer>();
for(int x : nums2){
if(set.contains(x)){
set1.add(x);
}
}
int index = 0;
int[] nums = new int[set1.size()];
for(int e : set1) {
nums[index++] = e;
}
return nums;
}
2.两个数组的交集 II(Easy,题号:350)
第1次
题目链接:两个数组的交集 II
题目描述:
给定两个数组,编写一个函数来计算它们的交集。

解题思路:
使用Map:使用一个Map,先将nums1中的元素作为键Key放到map中,值Value为频次(通过获取上一个Value值+1的方式来得到),遍历nums2中元素,看是否在map中,如果在,则将其存入list中,最后将list转化为数组。
代码:
使用Map:
public int[] intersect(int[] nums1, int[] nums2) {
Map<Integer,Integer> map = new HashMap<Integer,Integer>();
for(int i=0; i < nums1.length; i++){
if(map.containsKey(nums1[i])){
map.put(nums1[i],map.get(nums1[i]) + 1);
}
else {
map.put(nums1[i],1);
}
}
List<Integer> list = new ArrayList<Integer>();
for(int i=0; i < nums2.length; i++){
if(map.containsKey(nums2[i])&& map.get(nums2[i]) > 0){
list.add(nums2[i]);
map.put(nums2[i],map.get(nums2[i])-1);
}
}
int[] array = new int[list.size()];
for(int i=0; i < array.length; i++){
array[i] = list.get(i);
}
return array;
}
3.有效的字母异位词(Easy,题号:242)
第1次
题目链接:有效的字母异位词
题目描述:
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。

解题思路:通过map,先将一个字符串以字符的方式放入map中,然后再遍历遍历另一个字符串,若map中包含对应字符串,则将其value-1,最后将value值为0的键值对删除。
代码:
public boolean isAnagram(String s, String t) {
Map<Character,Integer> map = new HashMap<Character,Integer>();
for(int i=0; i < s.length(); i++){
if(map.containsKey(s.charAt(i)))
map.put(s.charAt(i),map.get(s.charAt(i))+1);
else
map.put(s.charAt(i),1);
}
for(int i=0; i < t.length(); i++){
if(map.containsKey(t.charAt(i))){
map.put(t.charAt(i),map.get(t.charAt(i))-1);
}
else
return false;
if(map.get(t.charAt(i)) == 0)
**加粗样式** map.remove(t.charAt(i));
}
return map.isEmpty();
}
4.快乐数(Easy,题号:202)
第1次
题目链接:快乐数
题目描述:
编写一个算法来判断一个数是不是“快乐数”。
一个“快乐数”定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是无限循环但始终变不到 1。如果可以变为 1,那么这个数就是快乐数。

解题思路:使用Set,将数字拆分求和使用递归。
代码:
public boolean isHappy(int n) {
Set<Integer> set = new HashSet<Integer>();
while(!set.contains(n)){
set.add(n);
n = fun(n);
if(n == 1)
return true;
}
return false;
}
public int fun(int n){
if(n == 0)
return 0;
int a = n%10;
return a*a + fun(n/10);
}
class Solution {
public boolean isHappy(int n) {
Set<Integer> set = new HashSet<Integer>();
int x = pow(n);
while(!set.contains(x)){
set.add(x);
x = pow(x);
if(x == 1)
return true;
}
return false;
}
public int pow(int n){
if(n/10 == 0)
return n*n;
int res = 0;
while(n/10 > 0){
res = res + (n%10)*(n%10);
n = n/10;
}
res = res + n*n;
return res;
}
}
5.单词规律(Easy,题号:290)
第2次
题目链接:单词规律
题目描述:
给定一种规律 pattern 和一个字符串 str ,判断 str 是否遵循相同的规律。
这里的 遵循 指完全匹配,例如, pattern 里的每个字母和字符串 str 中的每个非空单词之间存在着双向连接的对应规律。

解题思路:使用map,同时将str字符串使用split函数以正则表达式方式分割成字符串数组,然后使用一次for循环遍历。
代码:
public boolean wordPattern(String pattern, String str) {
if(pattern == null || str == null){
return false;
}
Map<Character,String> map = new HashMap<Character,String>();
String[] arr_s = str.split(" ");
if(pattern.length() != arr_s.length)
return false;
for(int i=0; i < pattern.length(); i++){
if(map.containsKey(pattern.charAt(i))){
if(!arr_s[i].equals(map.get(pattern.charAt(i))))
return false;
}
else {
if (map.containsValue(arr_s[i]))
return false;
else
map.put(pattern.charAt(i),arr_s[i]);
}
}
return true;
}
6.同构字符串(Easy,题号:205)
第1次
题目链接:同构字符串
题目描述:
给定两个字符串 s 和 t,判断它们是否是同构的。
如果 s 中的字符可以被替换得到 t ,那么这两个字符串是同构的。
所有出现的字符都必须用另一个字符替换,同时保留字符的顺序。两个字符不能映射到同一个字符上,但字符可以映射自己本身。

解题思路:使用map集合,遍历到一对s.charAt(i)和t.charAt(i),看看以s.charAt(i)为Key的map中有没有,若有,判断其Value是否为t.charAt(i),不是则返回false;若没有,判断map中是否有以t.charAt(i)为Value的值,若有,判断其Key是否为s.charAt(i),不是则返回false。
代码:
public boolean isIsomorphic(String s, String t) {
if(s.length() == 0 && t.length() == 0)
return true;
Map<Character,Character> map = new HashMap<Character,Character>();
for(int i=0; i < s.length(); i++){
if(map.containsKey(s.charAt(i))){
if(map.get(s.charAt(i)) != t.charAt(i)){
return false;
}
}
else {
if(map.containsValue(t.charAt(i)))
return false;
map.put(s.charAt(i),t.charAt(i));
}
}
return true;
}
7.两数之和(Easy,题号:1)
第1次
题目链接:两数之和
题目描述:
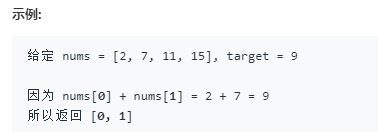
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
解题思路:
O(N^2):暴力解法,使用双层for循环进行遍历;
O(N):使用Map数据结构,nums[i]作为键,索引i作为值,判断Map里有没有target-nums[i],若有,直接返回,若没有,将nums[i]添加到Map中。
代码:
O(N^2):
public int[] twoSum(int[] nums, int target) {
int[] arr = new int[2];
for(int i=0; i < nums.length; i++){
for(int j = i + 1; j < nums.length ; j++){
if(target - nums[i] == nums[j]){
arr[0] = i;
arr[1] = j;
}
}
}
return arr;
}
O(N):
public int[] twoSum(int[] nums, int target) {
int[] arr = new int[2];
Map<Integer,Integer> map = new HashMap<Integer,Integer>();
for(int i=0; i < nums.length; i++){
if(map.containsKey(target-nums[i])){
arr[0] = map.get(target-nums[i]);
arr[1] = i;
return arr;
}
else
map.put(nums[i],i);
}
return arr;
}
8.三数之和(Medium,题号:15)
第1次
题目链接:三数之和
题目描述:
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。

解题思路:
代码:
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> lists = new ArrayList<List<Integer>>();
Set<List<Integer>> set = new HashSet<List<Integer>>();
for(int i=0; i < nums.length; i++){
Set<Integer> s1 = new HashSet<Integer>();
int target = 0-nums[i];
for(int j=i+1; j < nums.length; j++){
if(!s1.contains(target-nums[j])){
s1.add(nums[j]);
}
else{
List<Integer> list = new ArrayList<Integer>();
int min = Math.min(Math.min(nums[i],target-nums[j]),nums[j]);
int max = Math.max(Math.max(nums[i],target-nums[j]),nums[j]);
list.add(min);
list.add(0-min-max);
list.add(max);
set.add(list);
}
}
}
for(List<Integer> x : set){
lists.add(x);
}
return lists;
}
}