计算机视觉学习（九）：基于KNN分类法的手势识别

KNN算法原理：

KNN（k-nearest neighbor）是一个简单而经典的机器学习分类算法，通过度量”待分类数据”和”类别已知的样本”的距离（通常是欧氏距离）对样本进行分类。 
这话说得有些绕口，且来分解一番： 
（1）分类问题都是监督（supervised）问题，也就是说一定数量的样本类别是已知的。 
（2）既然我们已经有了一批分好类的样本，那么接下来的工作自然应该是通过已知样本训练分类器（通过调节分类器的参数，使分类器能够正确对训练样本分类），把分类器训练好以后用于对未知样本的分类（或类别预测）。 
看上去就是这么回事，问题的关键在于分类器的训练。 
但对于KNN分类器来说，事情并不是这个样子的。其实KNN并没有这么复杂。因为KNN并没有什么参数要调，换句话说，KNN其实并不需要训练！ 
作为最简单也最好理解的分类器，KNN只是假设数据都分布在欧式的特征空间内（以特征值为坐标区分不同样本的空间），然后我们恰好又知道全部数据在这个空间中的位置以及其中一部分数据的类别。那么现在我们怎么判断剩余那些数据的类别呢？ 
为了让分类进行下去，这里其实我们假设：空间中距离越近的点属于一类的可能性越大。 
有了这条“公理”，那事情就好办多了。我们只需要计算每个待分类数据到全部已知类别数据的距离就好了。如图： 

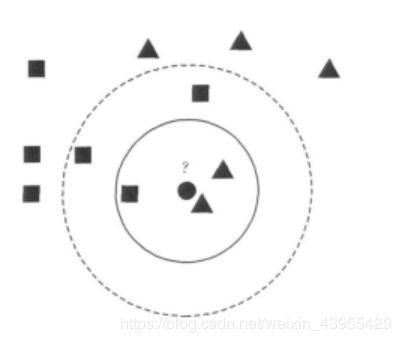
有正方形和三角形两个已知类，假如中间的圆形我们不知道它到底是三角形还是正方形。按照上面说的，我们可以正儿八经计算一下它到其他所有点的距离。在这里为了简便，我们目测一下发现它离旁边的三角形最近，好嘞，那么我们就把它归为三角形一类的。 
注意这里我们把未知点和离它最近的那一个点归为一类。这样的分类器，准确来说叫最近邻分类器（nearest-neighbor，NN）。这是KNN的特殊情况，是K=1的情况。 
那么K近邻，顾名思义，就是要一个未知点参考离它最近的前k个一直类别的点，看在这k个点里面，属于哪个类别的点最多，就认为未知点属于哪一类。还是上面的图，以圆形未知点为圆心，在实线画出的圆中，相当于k=3，也就是选了前三个离得最近的点，其中三角形2个，方形1个，所以未知点归到三角形一类。但是当考虑虚线范围内时，也就是k=5时，我们发现方形3个，三角形2个，所以这个时候未知点归到方形一类了。 
所以我们可以发现，不同的最近邻个数往往会导致不同的分类结果，一般来说，我们在实际应用中要根据实际情况和经验确定k的取值。

原理部分参考自博文：https://blog.csdn.net/weixin_41988628/article/details/80369850

使用KNN分类器实现分类一个简单的二维例子

创建二维点集的代码部分如下：

通过随机生成的方式，创建两个不同的二维点集class1和class2，每个点集有两类，分别是正态分布和绕环状分布，正态分布的范围主要通过代码中参数的调节实现，该参数越大，数据点范围越大，就更分散.

   绕环分布的范围，半径r决定了外圈数据集的集中程度，当r越大时，数据范围越大，就越分散

# -*- coding: utf-8 -*-
#生成点的过程
from numpy.random import randn
import pickle
from pylab import *

# create sample data of 2D points
# 打印两百个点
n = 200
# two normal distributions
# 两百个二维的点并通过*0.6限制他们的范围
class_1 = 0.8 * randn(n,2)
class_2 = 1.0 * randn(n,2) + array([5,1])
# 给他们分标签
labels = hstack((ones(n),-ones(n)))
# save with Pickle
#with open('points_normal.pkl', 'w') as f:
# 把他们存进
with open('points_normal_test.pkl', 'wb') as f:
    pickle.dump(class_1,f)
    pickle.dump(class_2,f)
    pickle.dump(labels,f)
# normal distribution and ring around it
print ("save OK!")
# 环状的数据
class_1 = 0.3 * randn(n,2)
r = 0.5 * randn(n,1) + 5
angle = 2*pi * randn(n,1)
class_2 = hstack((r*cos(angle),r*sin(angle)))
labels = hstack((ones(n),-ones(n)))
# save with Pickle
#with open('points_ring.pkl', 'w') as f:
with open('points_ring_test.pkl', 'wb') as f:
    pickle.dump(class_1,f)
    pickle.dump(class_2,f)
    pickle.dump(labels,f)
    
print ("save OK!")

使用KNN分类器对上面随机生成的点集分类代码部分如下：

为可视化所有测试数据点的分类，并展示分类器如何将两个不同的类分开，需要创建一个辅助函数classify(x,y,model=model)，以获取x和y二维坐标数组和分类器，并且返回一个预测的类标记数组array。然后把函数classify作为参数传递给实际的绘图函数plot_2D_boundary。

这个绘图函数需要一个分类器，并且用meshgrid()函数在一个网格上进行预测，网格的精度为0.1，每隔0.1采集一个点。分类器的等值线可以显示边界的位置，默认边界为零等值线。对于每一个类，用*画出分类正确的类，用O画出分类不正确的点

# -*- coding: utf-8 -*-
import pickle
from pylab import *
from PCV.classifiers import knn
from PCV.tools import imtools

pklist=['points_normal.pkl','points_ring.pkl']

figure()

# load 2D points using Pickle
# 枚举前面的两个元素
for i, pklfile in enumerate(pklist):
    with open(pklfile, 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)
    # load test data using Pickle
    with open(pklfile[:-4]+'_test.pkl', 'rb') as f:
        class_1 = pickle.load(f)
        class_2 = pickle.load(f)
        labels = pickle.load(f)

#knn分类器
    model = knn.KnnClassifier(labels,vstack((class_1,class_2)))
    # test on the first point
    print (model.classify(class_1[0]))

    #define function for plotting
    def classify(x,y,model=model):
        return array([model.classify([xx,yy]) for (xx,yy) in zip(x,y)])

    # lot the classification boundary
    subplot(1,2,i+1)
    # 画分界线
    imtools.plot_2D_boundary([-6,6,-6,6],[class_1,class_2],classify,[1,-1])
    titlename=pklfile[:-4]
    title(titlename)
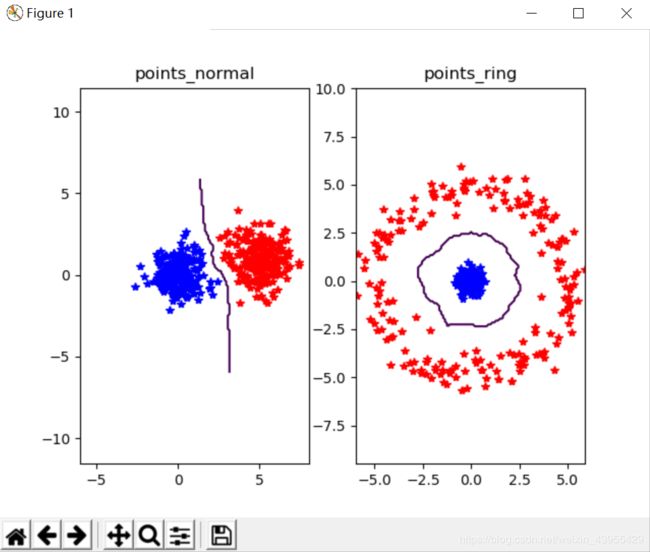
show()

使用以上代码运行出来的结果图如下，分类的结果较好，数据集密集分布但没有出现错分的情况

 

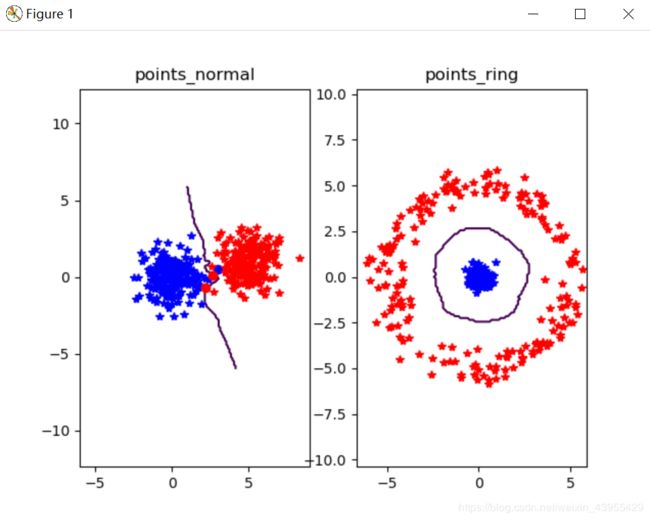
   下面将正态分布的范围调的更密集一些，把正态分布点集范围代码修改为如下形式

class_1 = 0.8 * randn(n,2)
class_2 = 1.0 * randn(n,2) + array([5,1])

发现分类结果有错分的情况，错分的点用圆圈表示。

图像稠密（dense）sift特征的实现

代码如下：

# -*- coding: utf-8 -*-
from PCV.localdescriptors import sift, dsift
from pylab import  *
from PIL import Image

dsift.process_image_dsift('gesture/wenwen.jpg','wenwen.dsift',90,40,True)
#读取dsif文件
l,d = sift.read_features_from_file('wenwen.dsift')
im = array(Image.open('gesture/wenwen.jpg'))
sift.plot_features(im,l,True)
title('dense SIFT')
show()

运行的结果图如下：

上述代码dsift.process_image_dsift('gesture/wenwen.jpg','wenwen.dsift',90,40,True)中90表示圈的大小，40表示步长，当保持圈的大小不变，将步长变大成80时的结果图如下：

上述结果表明在圆圈大小不变的情况下，随着步长的增大圆圈中心点之间的距离越大

图像分类--手势识别的实现

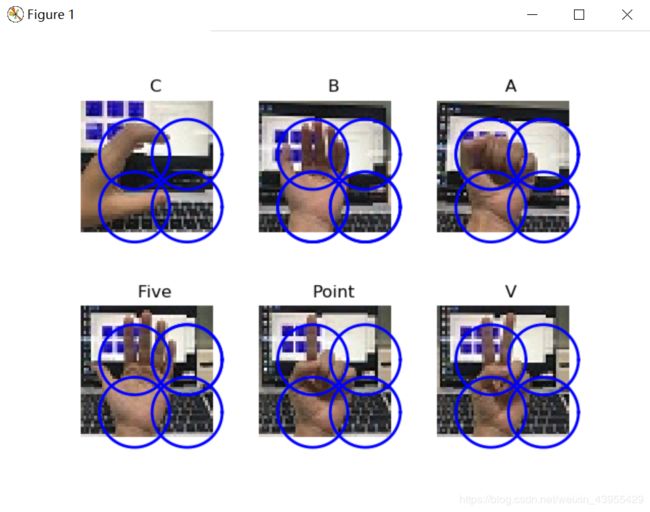
可视化带有描述子的手势图像代码如下：

用上面测试的稠密SIFT描述子来表示这些手势图像，并将测试数据集记录进数据库。代码会对指定的图像创建一个后缀为.dsift的特征文件

# -*- coding: utf-8 -*-
import os
from PCV.localdescriptors import sift, dsift
from pylab import  *
from PIL import Image

imlist=['gesture/wen/C-uniform02.jpg','gesture/wen/B-uniform01.jpg',
        'gesture/wen/A-uniform01.jpg','gesture/wen/Five-uniform01.jpg',
        'gesture/wen/Point-uniform01.jpg','gesture/wen/V-uniform01.jpg']

figure()
for i, im in enumerate(imlist):
    print (im)
    dsift.process_image_dsift(im,im[:-3]+'dsift',40,20,True)
    l,d = sift.read_features_from_file(im[:-3]+'dsift')
    dirpath, filename=os.path.split(im)
    im = array(Image.open(im))
    #显示手势含义title
    titlename=filename[:-14]
    subplot(2,3,i+1)
    sift.plot_features(im,l,True)
    title(titlename)
show()

运行的结果如下：

通过训练的数据识别出手势的代码如下：

运行完后结果会用显示正确率对于给定的测试集有多少图像是正确分类的，但是它并没有告诉我们哪些手势难以分类，或者犯哪些错误。这时，我们可以通过混淆矩阵来显示错误分类的情况。混淆矩阵是一个可以显示每类有多少个样本被分在每一类中的矩阵，它可以显示错误的分布情况，以及哪些类是经常相互“混淆”的

# -*- coding: utf-8 -*-
from PCV.localdescriptors import dsift
import os
from PCV.localdescriptors import sift
from pylab import *
from PCV.classifiers import knn

def get_imagelist(path):
    """    Returns a list of filenames for
        all jpg images in a directory. """
#获取图片的路径
    return [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.jpg')]

def read_gesture_features_labels(path):
    # create list of all files ending in .dsift
    featlist = [os.path.join(path,f) for f in os.listdir(path) if f.endswith('.dsift')]
    # read the features
    features = []
    for featfile in featlist:
        l,d = sift.read_features_from_file(featfile)
        features.append(d.flatten())
    features = array(features)
    # create labels
    labels = [featfile.split('/')[-1][0] for featfile in featlist]
    return features,array(labels)

def print_confusion(res,labels,classnames):
    n = len(classnames)
    # confusion matrix
    class_ind = dict([(classnames[i],i) for i in range(n)])
    confuse = zeros((n,n))
    for i in range(len(test_labels)):
        #是正确的类别就加一
        confuse[class_ind[res[i]],class_ind[test_labels[i]]] += 1
    print ('Confusion matrix for')
    print (classnames)
    print (confuse)

filelist_train = get_imagelist('gesture/train')
filelist_test = get_imagelist('gesture/test')
imlist=filelist_train+filelist_test

# process images at fixed size (50,50)
for filename in imlist:
    featfile = filename[:-3]+'dsift'
    dsift.process_image_dsift(filename,featfile,10,5,resize=(50,50))

features,labels = read_gesture_features_labels('gesture/train/')
test_features,test_labels = read_gesture_features_labels('gesture/test/')
classnames = unique(labels)

# test kNN
k = 1
knn_classifier = knn.KnnClassifier(labels,features)
res = array([knn_classifier.classify(test_features[i],k) for i in
range(len(test_labels))])
# accuracy
acc = sum(1.0*(res==test_labels)) / len(test_labels)
print ('Accuracy:', acc)

print_confusion(res,test_labels,classnames)
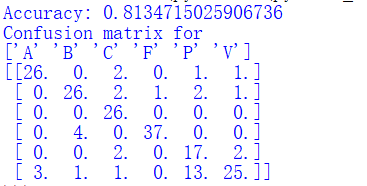
# 结果竖着看，其他数值表示错判的类别

运行的结果如下：

结果显示分类的正确率达到81.3%

混淆矩阵竖着看，比如A列，分类正确的有26，将A分错成V有三个

A、B、C、F、V的分类结果都比较好，错误率较低

而P类错分成V的概率很高