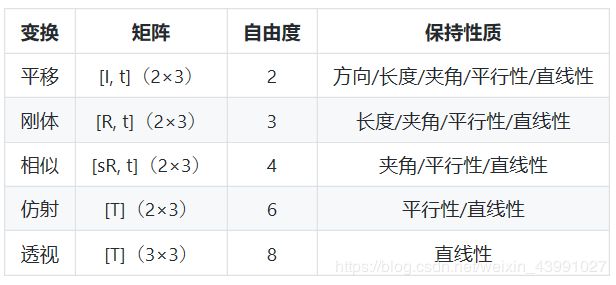
图像几何变换原理
图像变换原理

在三维中,通过光源照射下,不断变换光源,则在投影中得到不同的结果。
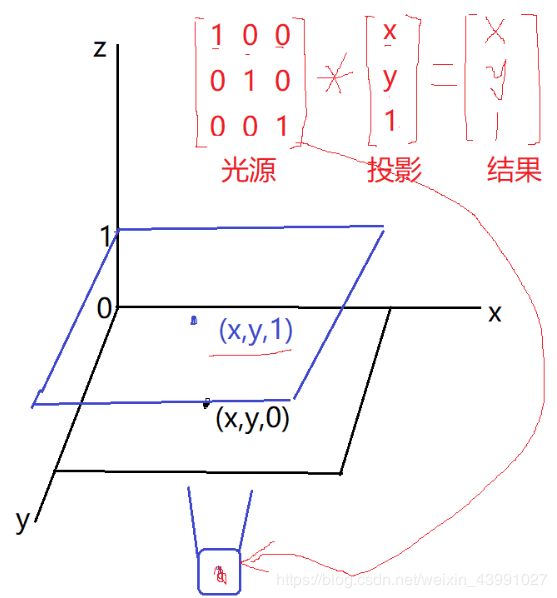
1. 缩放
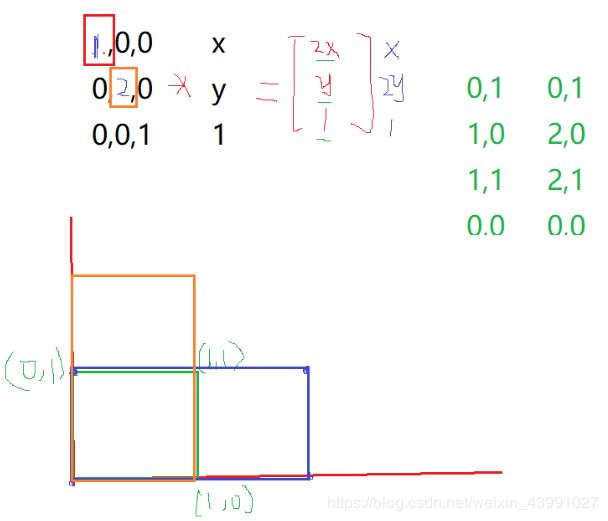
只变换矩阵的光源的位置,把光源拉近放远,则投影得到缩放的图像,达到调整图像大小的作用,下面示意图是按比例缩放的原理。
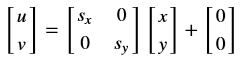
import cv2
img = cv2.imread('drawing.jpg')
# 按照指定的宽度、高度缩放图片
res = cv2.resize(img, (132, 150))
# 按照比例缩放,如x,y轴均放大一倍 interpolation:指定插值方式
res2 = cv2.resize(img, None, fx=2, fy=2, interpolation=cv2.INTER_LINEAR)
cv2.imshow('shrink', res), cv2.imshow('zoom', res2)
cv2.waitKey(0)2.平移
只变换矩阵的第三列的位置的数据,则投影得到平移的图像。

平移效果:

用仿射变换函数实现平移:
# 平移图片
import numpy as np
rows, cols = img.shape[:2]
# 定义平移矩阵,需要是numpy的float32类型
# x轴平移100,y轴平移50
M = np.float32([[1, 0, 100], [0, 1, 50]])
# 用仿射变换实现平移
dst = cv2.warpAffine(img, M, (cols, rows))
cv2.imshow('shift', dst)
cv2.waitKey(0)3.拉伸
4. 旋转
如果是以原点旋转,那么就直接套公式,计算旋转数据
如果是图片的中心或是中间的其他的点,作为旋转点,那么矩阵要做4步相乘,即先平移,再旋转,再平移。

旋转是坐标轴方向饶原点旋转一定的角度θ,自由度为1,不包含平移,如顺时针旋转可以表示为: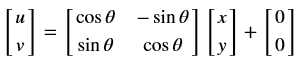
用仿射变换实现的,因此也需要定义一个变换矩阵。OpenCV直接提供了 cv2.getRotationMatrix2D()函数来生成这个矩阵,该函数有三个参数:
参数1:图片的旋转中心
参数2:旋转角度(正:逆时针,负:顺时针)
参数3:缩放比例,0.5表示缩小一半
# 45°旋转图片并缩小一半
M = cv2.getRotationMatrix2D((cols / 2, rows / 2), 45, 0.5)
dst = cv2.warpAffine(img, M, (cols, rows))
cv2.imshow('rotation', dst)
cv2.waitKey(0)5.仿射变换
基本的图像变换就是二维坐标的变换:从一种二维坐标(x,y)到另一种二维坐标(u,v)的线性变换:
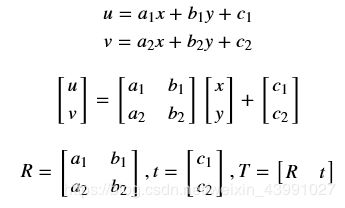
矩阵T(2×3)就称为仿射变换的变换矩阵,R为线性变换矩阵,t为平移矩阵,简单来说,仿射变换就是线性变换+平移。变换后直线依然是直线,平行线依然是平行线,直线间的相对位置关系不变,因此非共线的三个对应点便可确定唯一的一个仿射变换,线性变换4个自由度+平移2个自由度→仿射变换自由度为6。
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('drawing.jpg')
rows, cols = img.shape[:2]
# 变换前的三个点
pts1 = np.float32([[50, 65], [150, 65], [210, 210]])
# 变换后的三个点
pts2 = np.float32([[50, 100], [150, 65], [100, 250]])
# 生成变换矩阵
M = cv2.getAffineTransform(pts1, pts2)
dst = cv2.warpAffine(img, M, (cols, rows))
plt.subplot(121), plt.imshow(img), plt.title('input')
plt.subplot(122), plt.imshow(dst), plt.title('output')
plt.show()注: 三个点我已经在图中标记了出来
6.翻转
翻转是x或y某个方向或全部方向上取反,自由度为2,比如这里以垂直翻转为例: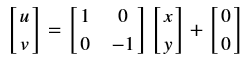
7.刚体变换
旋转+平移也称刚体变换(Rigid Transform),就是说如果图像变换前后两点间的距离仍然保持不变,那么这种变化就称为刚体变换。刚体变换包括了平移、旋转和翻转,自由度为3。变换矩阵可以表示为:

由于只是旋转和平移,刚体变换保持了直线间的长度不变,所以也称欧式变换(变化前后保持欧氏距离)。
8.相似变化
相似变换又称缩放旋转,相似变换包含了旋转、等比例缩放和平移等变换,自由度为4。在OpenCV中,旋转就是用相似变换实现的:
若缩放比例为scale,旋转角度为θ,旋转中心是$ (center_x,center_y) $,则仿射变换可以表示为:

相似变换相比刚体变换加了缩放,所以并不会保持欧氏距离不变,但直线间的夹角依然不变。
透视变化
前面仿射变换后依然是平行四边形,并不能做到任意的变换。
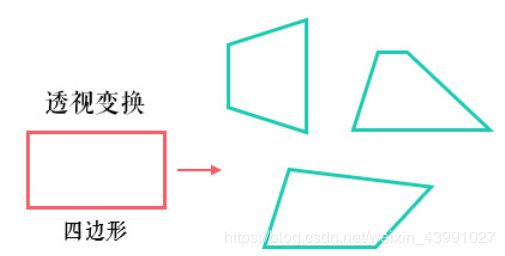
是将二维的图片投影到一个三维视平面上,然后再转换到二维坐标下,所以也称为投影映射(Projective Mapping)。简单来说就是二维→三维→二维的一个过程。
透视变换相比仿射变换更加灵活,变换后会产生一个新的四边形,但不一定是平行四边形,所以需要非共线的四个点才能唯一确定,原图中的直线变换后依然是直线。因为四边形包括了所有的平行四边形,所以透视变换包括了所有的仿射变换。
OpenCV中首先根据变换前后的四个点用cv2.getPerspectiveTransform()生成3×3的变换矩阵,然后再用cv2.warpPerspective()进行透视变换。
img = cv2.imread('card.jpg')
# 原图中卡片的四个角点
pts1 = np.float32([[148, 80], [437, 114], [94, 247], [423, 288]])
# 变换后分别在左上、右上、左下、右下四个点
pts2 = np.float32([[0, 0], [320, 0], [0, 178], [320, 178]])
# 生成透视变换矩阵
M = cv2.getPerspectiveTransform(pts1, pts2)
# 进行透视变换,参数3是目标图像大小
dst = cv2.warpPerspective(img, M, (320, 178))
plt.subplot(121), plt.imshow(img[:, :, ::-1]), plt.title('input')
plt.subplot(122), plt.imshow(dst[:, :, ::-1]), plt.title('output')
plt.show()变化自由度:
参考博客:https://www.jianshu.com/p/c4a969bc0106
https://github.com/ex2tron/OpenCV-Python-Tutorial/tree/master/番外篇05.%20仿射变换和透视变换原理