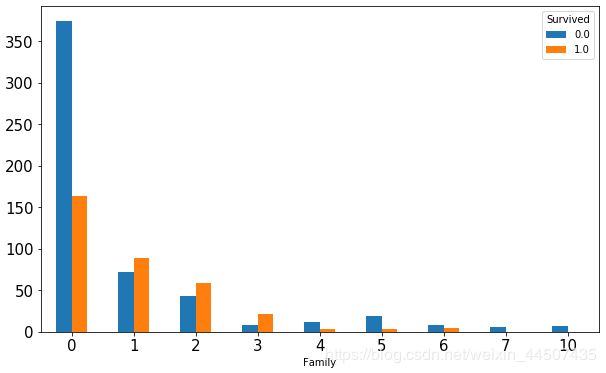Kaggle实战:Titanic生存预测(Top 8%)

准备入行数据分析领域,最近一直在学习数据分析的相关课程,刚刚将numpy以及pandas告一段落了,迫不及待的上Kaggle找个实战项目练练手,接下来将详细的过程记录如下。
文章目录
- 1.数据概览
- 2.缺失值处理
- Embarked缺失值填充
- Fare缺失值填充
- Age缺失值填充
- 3.数据分析
- Pclass对生存率的影响
- Name对生存率的影响
- Sex对生存率的影响
- 家庭规模对生存率的影响
- Age对生存率的影响
- Embarked对生存率的影响
- 4.模型建立
- 特征提取及哑变量编码
- random_state学习曲线
- max_depth学习曲线
- min_samples_split学习曲线
- min_samples_leaf学习曲线
- min_impurity_decrease学习曲线
- 预测结果输出
- 5.不足与展望
- 参考文献
1.数据概览
先导入数据分析需要的基本库:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
读入数据,数据分为train.csv(训练集)和test.csv(测试集)两部分,其中测试集数据不带有标签,这里将两部分数据一次性读入并合并,将PassengerId作为数据的索引:
train_data = pd.read_csv('data/train.csv',index_col = 'PassengerId')
test_data = pd.read_csv('data/test.csv',index_col = 'PassengerId')
data_all = pd.concat([train_data,test_data],axis=0)
看一下数据的基本概况:
data_all.tail()
#1~891训练集,891~1309测试集
data_all.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 1309 entries, 1 to 1309
Data columns (total 11 columns):
Age 1046 non-null float64
Cabin 295 non-null object
Embarked 1307 non-null object
Fare 1308 non-null float64
Name 1309 non-null object
Parch 1309 non-null int64
Pclass 1309 non-null int64
Sex 1309 non-null object
SibSp 1309 non-null int64
Survived 891 non-null float64
Ticket 1309 non-null object
dtypes: float64(3), int64(3), object(5)
memory usage: 122.7+ KB
各字段的含义如下:
'''
passengerId:乘客ID
survived:是否被救获
Pclass:乘客等级(舱位等级分为1/2/3等)
Name:乘客姓名
Sex:乘客性别
Age:乘客年龄
SibSp:siblings&spoused,该乘客在船上的堂兄弟妹/配偶人数
Parch:该乘客在船上的父母/孩子人数
Ticket:船票信息
Fare:票价
Cabin:客舱
Embarked:登船港口
出发地点:S=英国南安普顿Southampton
途径地点1:C=法国 瑟堡市Cherbourg
途径地点2:Q=爱尔兰 昆士敦Queenstown
'''
Cabin、Embarked、Age、Fare字段存在缺失值,Survived的缺失主要是由于我们将训练集与测试集整合在一起的缘故。接下来对缺失数据进行分析并填充。
2.缺失值处理
Cabin字段缺失数据1014条,缺失比例达77.5%,缺失比例过大,盲目填充可能会导致数据中的错误信息增加,本次分析将Cabin特征舍弃。接下来对Embarked、Fare、Age三个字段进行分别填充。
Embarked缺失值填充
原始数据中Embarked字段仅有两处缺失,将缺失的数据提取出来,看看其其他特征:
#查看Embarked缺失的两列情况
data_all.loc[data_all.loc[:,'Embarked'].isnull(),:]

缺失的两条数据ID分别为62和830,两个乘客的票号,舱位等级、票价及船舱号都相同,由此分析应该是一同上船的。现在以票价(Fare)和舱位等级(Pclass)作为突破口,假设同一处上船的票价相同。
#62号乘客和830号乘客的票价Fare都是80, Pclass都是1,那么先假设票价、客舱和等级相同的乘客是在同一个登船港口登船。
data_all.groupby(['Embarked','Pclass'])['Fare'].median()
Embarked Pclass
C 1 76.7292
2 15.3146
3 7.8958
Q 1 90.0000
2 12.3500
3 7.7500
S 1 52.0000
2 15.3750
3 8.0500
Name: Fare, dtype: float64
从上述分析可以看出,从C(法国 瑟堡市Cherbourg)登船的乘客票价的中位数与80最为接近,因此将Embarked的缺失字段用C填补。
#Embarked为C且Pclass为1的乘客的Fare中位数为80。因此可以将缺失的Embarked值设置为“C”
data_all['Embarked'].fillna('C',inplace = True)
Fare缺失值填充
Fare字段共缺失一条数据,看看缺失数据其他特征的情况:
#Fare值的缺失位置和相关信息
data_all.loc[data_all['Fare'].isnull(),:]

与之前的思路相同,查看从S(英国南安普顿Southampton)上船的3等舱的票价中位数:
data_all.groupby(['Embarked','Pclass'])['Fare'].median()
Embarked Pclass
C 1 78.2667
2 15.3146
3 7.8958
Q 1 90.0000
2 12.3500
3 7.7500
S 1 52.0000
2 15.3750
3 8.0500
Name: Fare, dtype: float64
从S港登船的乘客,票价的中位数为8.05,用该值填充缺失值:
#S登船港口上船且Pclass为3的乘客费用Fare的中位数为8.05,因此Fare的空缺值补充为8.05。
data_all['Fare'].fillna(8.05,inplace = True)
Age缺失值填充
先看一下未填充之前Age的分布情况:
#age原始数据的分布情况
data_all['Age'].hist(bins = 10,grid = False,density = True,figsize = (10,6))

此处,因为Age的缺失数据有263条,缺失比例为20.1%,如果全部简单的采用均值填补,会使得数据的分布发生较大的变化。因此,考虑使用随机森林对缺失值进行填补。这里选择Sex,Embarked,Fare,SibSp,Parch,Pclass作为缺失值填补的预测特征。首先对非数值型数据进行哑变量编码处理。
#age先考虑用随机森林填充
#选择的预测变量Sex,Embarked,Fare,SibSp,Parch,Pclass
from sklearn.preprocessing import OneHotEncoder
data_ = data_all.copy()
X_co = data_[['Sex','Embarked']]#需要编码的变量Sex,Embarked
enc = OneHotEncoder().fit(X_co)
result = OneHotEncoder().fit_transform(X_co).toarray()
enc.get_feature_names()
array(['x0_female', 'x0_male', 'x1_C', 'x1_Q', 'x1_S'], dtype=object)
创建预测需要的特征矩阵X:
#拼接填补缺失值用的特征矩阵
X = pd.concat([data_all.loc[:,['Fare','SibSp','Parch','Pclass']],pd.DataFrame(result,index = np.arange(1,1310),columns = ['female','male','C','Q','S'])],axis=1)
X.head()
#标签
Y = data_all['Age']
划分训练集,测试集(其中Age字段没有缺失的行的集合,为训练集;Age字段存在缺失的行的集合为测试集)
#划分测试集,训练集
Y_tr = Y[Y.notnull()]
Y_te = Y[Y.isnull()]
X_tr = X.loc[Y_tr.index,:]
X_te = X.loc[Y_te.index,:]
导入随机森林模型,训练并输出预测结果
#随机森林填补缺失值
from sklearn.ensemble import RandomForestRegressor
rfr = RandomForestRegressor(n_estimators=1000,random_state=0)#实例化
rfr.fit(X_tr,Y_tr)#训练模型
Y_te = rfr.predict(X_te)#预测结果输出
data_.loc[data_['Age'].isnull(),'Age'] = Y_te
看一下,缺失值填充前后数据分布的变化情况
plt.subplot(121)
data_all['Age'].hist(bins = 10,grid = False,density = True,figsize = (10,6))
plt.title('before fillna')
plt.subplot(122)
data_['Age'].hist(bins=10,grid = False,density = True,figsize = (10,6))
plt.title('after fillna')
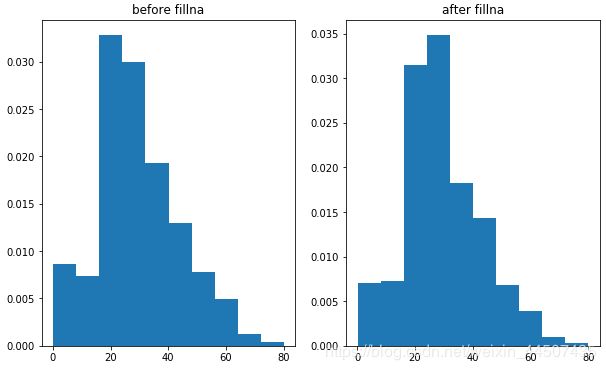
20~30年龄段的数据分布占比较填充前有明显变化,25 ~ 30岁的人数占比增多,其余年龄段的分布与之前基本相同。
3.数据分析
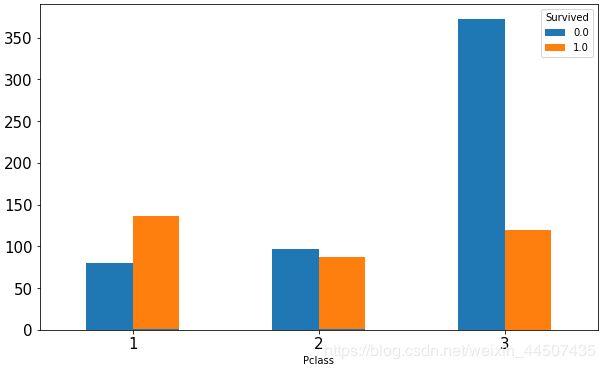
Pclass对生存率的影响
数据分组:
print(data_all.groupby(['Pclass','Survived'])['Survived'].count())
print(data_all.groupby(['Pclass'])['Survived'].mean())
Pclass Survived
1 0.0 80
1.0 136
2 0.0 97
1.0 87
3 0.0 372
1.0 119
Name: Survived, dtype: int64
Pclass
1 0.629630
2 0.472826
3 0.242363
Name: Survived, dtype: float64
分组数据可视化:
Pclass_count = data_all.groupby(['Pclass','Survived'])['Survived'].count()
Pclass_mean = data_all.groupby(['Pclass'])['Survived'].mean()
Pclass_count.unstack().plot(kind = 'bar',figsize = (10,6),fontsize = 15,rot = 0)#分组后的多重索引数据可通过unstack方法解除一重索引。
Pclass_mean.plot(kind = 'bar',figsize = (10,6),fontsize = 15,rot =0)
Pclass_mean.plot(kind = 'bar',figsize = (15,6),fontsize = 15,rot =0)

一等舱的生存率明显高于其他两个等级的舱。三等舱的生存率还不足30%。
Name对生存率的影响
Name字段是一个比较复杂的字段,在该数据量下,名字基本不会存在重复的现象,因此若不对字段加以处理就进行分析,会对分析结果造成较大影响。仔细观察Name字段的特点,名字中的称谓(Title)存在一定的重复性,且称谓可以一定程度上表示该乘客的社会地位或职业情况,因此本次分析中选取Title来代替Name作为新的特征。
先创建一个空列表,将原始数据中Name字段的Title分隔出来并存入新的列表中
title_list = []
for i in data_all['Name']:
title_list.append(i.split(',')[1].split('.')[0].strip())
pd.Series(title_list).value_counts()
Mr 757
Miss 260
Mrs 197
Master 61
Dr 8
Rev 8
Col 4
Major 2
Mlle 2
Ms 2
Don 1
the Countess 1
Mme 1
Dona 1
Sir 1
Jonkheer 1
Capt 1
Lady 1
dtype: int64
所有的Title共18种,我们将其做一个整合,并将提取出的Title做一个映射:
title_mapDict = {'Capt':'Officer'
,"Col":"Officer"
,"Major":"Officer"
,"Jonkheer":"Royalty"
,"Don":"Royalty"
,'Dona':'Royalty'
,"Sir":"Royalty"
,"Dr":"Officer"
,"Rev":"Officer"
,"the Countess":"Royalty"
,"Mme":"Mrs"
,"Mlle":"Miss"
,"Ms":"Mrs"
,"Mr":"Mr"
,"Mrs" :"Mrs"
,"Miss" :"Miss"
,"Master" :"Officer"
,"Lady" :"Royalty"
}
title_ = pd.Series(title_list).str.strip().map(title_mapDict)
#注意!提取出的Title中存在空格,一定要用strip()方法去除空格后在映射,否则会失败!
看一下各Title生存人数情况
data_all['Name'] = title_
Name_count = data_all.groupby(['Name','Survived'])['Survived'].count()
print(Name_count)
Name_count.unstack().plot(kind = 'bar',figsize = (10,6),fontsize = 15,rot =0,stacked = True)
Name Survived
Miss 0.0 116
1.0 68
Mr 0.0 317
1.0 200
Mrs 0.0 75
1.0 52
Officer 0.0 37
1.0 21
Royalty 0.0 4
1.0 1
Name: Survived, dtype: int64
Name_mean = data_all.groupby(['Name'])['Survived'].mean()
print(Name_mean)
Name_mean.plot(kind = 'bar',figsize = (10,6),fontsize = 15,rot =0)
Name
Miss 0.369565
Mr 0.386847
Mrs 0.409449
Officer 0.362069
Royalty 0.200000
Name: Survived, dtype: float64

女性的生存率相对来说高一些,而Royalty的生存率较低。接下来进一步探讨性别对生存概率的影响。
Sex对生存率的影响
生存人数情况
Sex_count = data_all.groupby(['Sex','Survived'])['Survived'].count()
print(Sex_count)
Sex_count.unstack().plot(kind = 'bar',figsize = (10,6),fontsize = 15,rot =0)
Sex Survived
female 0.0 81
1.0 233
male 0.0 468
1.0 109
Name: Survived, dtype: int64
Sex_mean = data_all.groupby(['Sex'])['Survived'].mean()
print(Sex_mean)
Sex_mean.plot(kind = 'bar',figsize = (10,6),fontsize = 15,rot =0)
Sex
female 0.742038
male 0.188908
Name: Survived, dtype: float64

这里就可以明显的看出,女性的生存率远高于男性。逃生的时候也是Women and Child First。
在看看不同舱位等级下男女生存概率:
#不等舱位等级,不同性别的生还概率
print('不同舱位等级的生还人数:\n',train_data.groupby(['Pclass','Sex','Survived'])['Survived'].count())
print('--------------------------')
print('不同舱位等级的生还概率:\n',train_data.groupby(['Pclass','Sex'])['Survived'].mean())
不同舱位等级的生还人数:
Pclass Sex Survived
1 female 0 3
1 91
male 0 77
1 45
2 female 0 6
1 70
male 0 91
1 17
3 female 0 72
1 72
male 0 300
1 47
Name: Survived, dtype: int64
--------------------------
不同舱位等级的生还概率:
Pclass Sex
1 female 0.968085
male 0.368852
2 female 0.921053
male 0.157407
3 female 0.500000
male 0.135447
Name: Survived, dtype: float64
train_data.groupby(['Pclass','Sex'])['Survived'].mean().unstack().plot(kind = 'bar',rot = 0,figsize = (10,6),fontsize = 15)
plt.xlabel('Pclass',fontdict = {'size' : 15})
plt.ylabel('Survived Rate',fontdict = {'size':15})
plt.legend(fontsize = 15)

可以看到一等舱的女性生存率高达96%,基本都存活下来了。而三等舱的男性只有13%的生还概率。(Rose获救,Jack牺牲,冥冥之中大数据看透了一切)
家庭规模对生存率的影响
原始数据中与家庭相关的字段有SibSp(该乘客在船上的堂兄弟妹/配偶人数)Parch(该乘客在船上的父母/孩子人数),我们将两个字段进行合并,创建一个新的Family字段,通过Family字段进行分析。
不同家庭规模的生存情况:
#家庭人口对生存的影响
data_all['Family'] = data_all['SibSp'] + data_all['Parch']
Family_count = data_all.groupby(['Family','Survived'])['Survived'].count()
print(Family_count)
Family_count.unstack().plot(kind = 'bar',figsize = (10,6),fontsize = 15,rot =0)
Family Survived
0 0.0 374
1.0 163
1 0.0 72
1.0 89
2 0.0 43
1.0 59
3 0.0 8
1.0 21
4 0.0 12
1.0 3
5 0.0 19
1.0 3
6 0.0 8
1.0 4
7 0.0 6
10 0.0 7
Name: Survived, dtype: int64
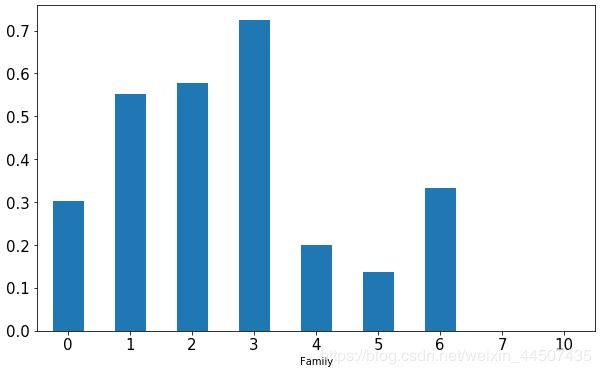
Family_mean = data_all.groupby(['Family'])['Survived'].mean()
print(Family_mean)
Family_mean.plot(kind = 'bar',figsize = (10,6),fontsize = 15,rot =0)
Family
0 0.303538
1 0.552795
2 0.578431
3 0.724138
4 0.200000
5 0.136364
6 0.333333
7 0.000000
10 0.000000
Name: Survived, dtype: float64
Age对生存率的影响
先看一下各年龄段的分布及生存概率情况:
#age对生存的影响
data_all.loc[data_all['Survived'] == 0,:]['Age'].hist(bins = 10,figsize = (10,6),label = 'Not Survived',grid = False)
data_all.loc[data_all['Survived'] == 1,:]['Age'].hist(bins = 10,figsize = (10,6),label = 'Survived',grid = False)
plt.legend()

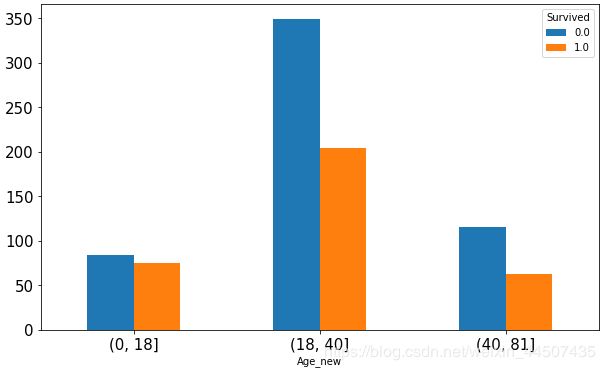
本次分析中考虑将年龄进行分箱处理,分为(0,18]、(18,40]、(40,81]三个区段,先看看每个年龄段存活人数的情况
#Age_new分箱
bins = [0,18,40,81]
Age_new = pd.cut(data_all['Age'],bins)
data_all['Age_new'] = Age_new
Age_count = data_all.groupby(['Age_new','Survived'])['Survived'].count()
print(Age_count)
Age_count.unstack().plot(kind = 'bar',figsize = (10,6),fontsize = 15,rot =0)
Age_new Survived
(0, 18] 0.0 84
1.0 75
(18, 40] 0.0 349
1.0 204
(40, 81] 0.0 116
1.0 63
Name: Survived, dtype: int64
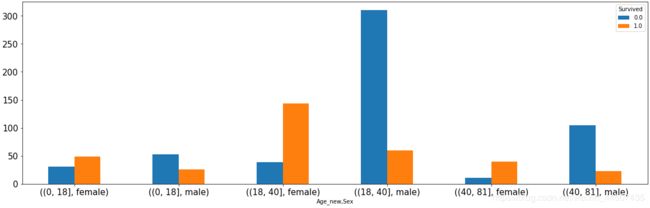
Age_new Sex Survived
(0, 18] female 0.0 31
1.0 49
male 0.0 53
1.0 26
(18, 40] female 0.0 39
1.0 144
male 0.0 310
1.0 60
(40, 81] female 0.0 11
1.0 40
male 0.0 105
1.0 23
Name: Survived, dtype: int64
Embarked对生存率的影响
存活人数情况
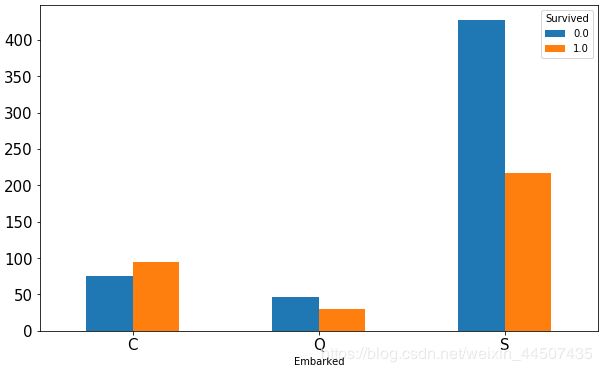
Embarked_count = data_all.groupby(['Embarked','Survived'])['Survived'].count()
print(Embarked_count)
Embarked_count.unstack().plot(kind = 'bar',figsize = (10,6),fontsize = 15,rot =0)
Embarked Survived
C 0.0 75
1.0 95
Q 0.0 47
1.0 30
S 0.0 427
1.0 217
Name: Survived, dtype: int64
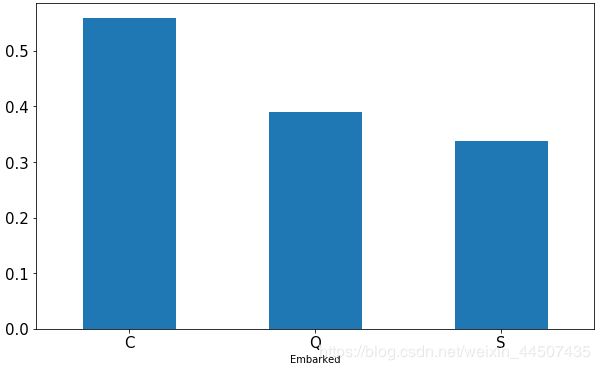
Embarked_mean = data_all.groupby(['Embarked'])['Survived'].mean()
print(Embarked_mean)
Embarked_mean.plot(kind = 'bar',figsize = (10,6),fontsize = 15,rot = 0)
4.模型建立
特征提取及哑变量编码
根据上述分析,我们选取Age_new、Embarked、Fare、Pclass、Sex、Family特征进行建模,其中Age_new、Embarked、Sex特征为非数值类型,需要先进行编码。
from sklearn.preprocessing import OneHotEncoder
X_code = data_all.loc[:,['Age_new','Embarked','Sex']]
ohe = OneHotEncoder().fit(X_code)
result_X_code = ohe.fit_transform(X_code).toarray()
ohe.get_feature_names()
array(['x0_(0, 18]', 'x0_(18, 40]', 'x0_(40, 81]', 'x1_C', 'x1_Q', 'x1_S',
'x2_female', 'x2_male'], dtype=object)
创建新的特征矩阵
new_col = ['(0, 18]','(18, 40]','(40, 81]','C','Q','S','female','male']
X = pd.concat([data_all.loc[:,['Fare','Pclass','Family']],pd.DataFrame(result_X_code,columns = new_col,index = np.arange(1,1310))],axis=1)
拆分训练集、测试集
Y_train = data_all.loc[1:891,'Survived']
Y_test = data_all.loc[892:1309,'Survived']
X_train = X.loc[1:891,:]
X_test = X.loc[892:1309,:]
导入建模需要的库
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score
from sklearn.tree import export_graphviz
import graphviz
random_state学习曲线
#random_state学习曲线
score = []
for i in range(1,300):
clf = DecisionTreeClassifier(random_state=i,criterion='entropy',max_depth=8)
score.append(cross_val_score(clf,X_train,Y_train,cv=10).mean())
print(max(score),score.index(max(score)))
plt.plot(np.arange(1,300),score)
0.8327840199750313 15
max_depth学习曲线
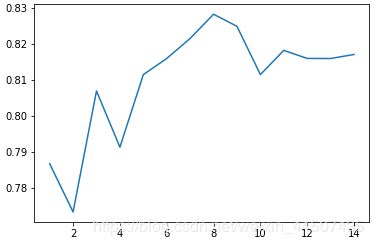
#max_depth学习曲线
score = []
for i in range(1,15):
clf = DecisionTreeClassifier(random_state=0,criterion='entropy',max_depth=i)
score.append(cross_val_score(clf,X_train,Y_train,cv=10).mean())
print(max(score),score.index(max(score)))
plt.plot(np.arange(1,15),score)
0.8282896379525594 7
min_samples_split学习曲线
#min_sample_split学习曲线
score = []
for i in range(1,15):
clf = DecisionTreeClassifier(random_state=15,criterion='entropy',max_depth=8,min_samples_split=i)
score.append(cross_val_score(clf,X_train,Y_train,cv=10).mean())
print(max(score),score.index(max(score)))
plt.plot(np.arange(1,15),score)
min_samples_leaf学习曲线
#min_sample_leaf学习曲线
score = []
for i in range(1,15):
clf = DecisionTreeClassifier(random_state=0,criterion='entropy',max_depth=8,min_samples_leaf=i)
score.append(cross_val_score(clf,X_train,Y_train,cv=10).mean())
print(max(score),score.index(max(score)))
plt.plot(np.arange(1,15),score)
0.8282896379525594 0
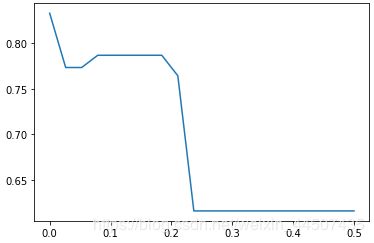
min_impurity_decrease学习曲线
#最小信息增益min_impurity_decrease
score = []
for i in np.linspace(0,0.5,20):
clf = DecisionTreeClassifier(random_state=16,criterion='entropy',max_depth=8,min_impurity_decrease=i)
score.append(cross_val_score(clf,X_train,Y_train,cv=10).mean())
print(max(score),score.index(max(score)))
plt.plot(np.linspace(0,0.5,20),score)
0.8327840199750313 0
预测结果输出
#预测结果
clf = DecisionTreeClassifier(random_state=16,criterion='entropy',max_depth=8)
clf.fit(X_train,Y_train)
Y_test = clf.predict(X_test)
result = pd.Series(Y_test,index=np.arange(892,1310))
result.to_csv(r'DecisionTreeClassifier.csv')
将输出结果提交到Kaggle,预测准确率0.80382,排名1167th,进入top 8%,还是比较满意的。

5.不足与展望
- 本次实战练习参考了前Top 2%的大佬文章(在参考文献中列出),发现在数据处理的思路方面还是有较大的欠缺。一味追求使用强学习模型并不一定能取得更好的结果,做好数据预处理与特征选择才是王道。
- 本次分析中Age字段的缺失值填充存在缺陷,填充后的数据分布与原始数据存在差异。且Age字段的分箱结果并没有十分突出各年龄段的生存概率差异,这一点后续有待改进。
- Name字段的映射分组没有很好的区分开样本,不同Title的样本生存概率差异不大。
参考文献
https://zhuanlan.zhihu.com/p/28802636