python--实现归并排序（分治策略）

分治算法总体思想：

分—将要求解的较大规模的问题分割成k个更小规模的子问题。

治—对这k个子问题分别求解。如果子问题的规模仍然不够 小，则再划分为k个子问题，如此递归的进行下去，直到问题 规模足够小，很容易求出其解为止。

合—将求出的小规模的问题的解合并为一个更大规模的问 题的解，自底向上逐步求出原来问题的解。

由于分治的过程中会使用到递归的概念，这里再过多的说一下递归的概念：

由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。直接或间接地调用自身的算法称为递归算法。用函数自身给出定义的函数称为递归函数。分治是一种思想，递归是一种手段。

递归函数的两个基本要素 ：1. 递归边界，也就是函数的初始值，每一个递归函数都必须具 备非递归定义的初始值，否则，递归函数就无法计算。 2. 递归关系式，用较小自变量的函数值来表示较大自变量的函数值，它是递归求解的依据，体现分治策略的核心要素。

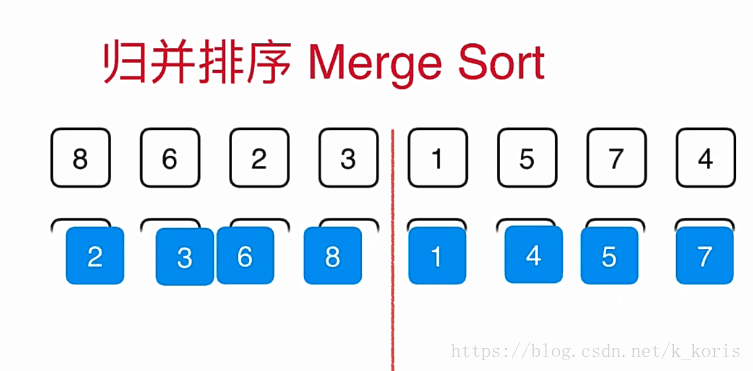
归并排序（Merge Sort）与快速排序思想类似：将待排序数据分成两部分，继续将两个子部分进行递归的归并排序；然后将已经有序的两个子部分进行合并，最终完成排序。排序过程大致如下：

1.利用分治思想将待排序列递归分成细度为1的子序列

2.此时，每个子序列只有一个元素，无需排序，两两进行简单的归并

3.归并到上一个层级后继续归并，归并到更高的层级

 4.直至归并完成

---

代码如下：

def mergesort(seq):
    mid = len(seq) // 2
    if len(seq) <= 1:
        return seq
    lft = mergesort(seq[:mid])
    rgt = mergesort(seq[mid:])
    res = []
    while lft and rgt:
        if lft[-1] >= rgt[-1]:
            res.append(lft.pop())
        else:
            res.append(rgt.pop())
    res.reverse()
    # 返回合并排序后的序列
    return lft + rgt + res

下次会为大家更新数字旋转矩阵的实现过程~