数据结构与算法分析（一）

数据结构与算法分析（一）

数据结构 + 算法 = 程序
数据结构主要研究组织大量数据的方法，算法分析是对算法运行的时间的评估。

第一章 基本概念

第一节 数据结构

1.1 基本术语和概念

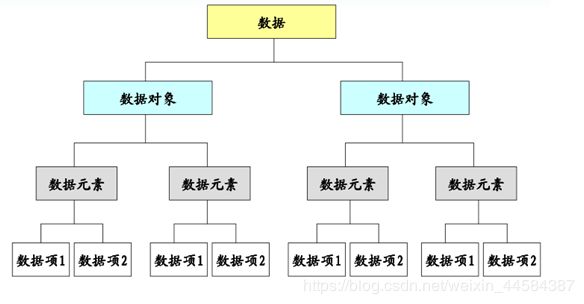
（1）数据（Data）：是指描述客观事物的符号，是计算机可以操作的对象，能被计算机识别，并输入给计算机处理的符号或符号集合。万物皆可为数据，不止局限于数字，字符，一个图像，一段视频都是数据。

（2）数据对象（data object）：是性质相同数据元素的集合，是数据的一个子集。例如所有的视频数据可以成为一个数据对象。

（3）数据元素（data element）：是数据的基本单位。也叫结点或记录。例如一个视频。

（4）数据项（data item）：是数据的最小单位。例如视频里的每一帧。

（5）数据结构（data structure）：是数据元素之间的组织方式。

1.2. 数据的逻辑结构

​ 逻辑结构（logical structure）：指反映数据元素之间的逻辑关系的数据结构，其中的逻辑关系是指数据元素之间的前后件关系，而与他们在计算机中的存储位置无关。

数据结构有四种不同的逻辑结构：

（1）集合结构：集合中的各个元素是平等的，元素之间没有任何联系，仅是共处于同一集合。

（2）线性结构：元素结构关系是一对一的，并且是一种先后的次序。

（3）树形结构：元素结构关系是一对多的，并且存在父子级。

（4）图形结构：元素结构关系是多对多的。

1.3 数据的存储结构

​ 存储结构（storage structure） 也成为物理结构（physical structure），是指数据的逻辑结构在计算机中的存储形式，一般可以反映数据元素之间的逻辑关系。

数据结构有两种不同的存储结构：

（1）顺序存储结构：把数据元素存储在地址连续的存储单元中，数据间的逻辑关系和物理关系是一致的。

（2）链式存储结构：把数据元素存储在任意的存储单元里，这组存储单元可以是连续的，也可以是不连续的。

1.4 抽象数据类型

抽象数据类型（abstract data type，ADT） 是一些操作的集合。描述数据类型的方法不依赖于具体实现，与存放的机器无关，与数据存储的物理结构无关，与实现操作的算法和编程语言无关，只描述数据对象集合相关操作集“是什么”，并不干涉“如何做到”。

表ADT 栈ADT 队列ADT

第二节 算法及性能分析

2.1 算法

算法（algorithm） 是一系列为特定问题而规定指令的集合。有以下特性：

• 输入，是指算法具有零个或多个输入。

• 输出，是指算法至少有一个或多个输出。

• 有穷性，是指算法在执行有限的步骤之后，自动结束而不是出现无限循环，并且每一个步骤在可接受的时间内完成。

• 确定性，是指相同输入只能有一个唯一的输出结果，不会出现二义性。

• 可行性，是指算法每一步骤都必须可行，能够通过有限的执行次数完成。

2.2时间复杂度

​ 算法的时间复杂度，也就是算法的时间量度，记作： T(n)=O(f(n))。它表示随问题规模 n的增大算法执行时间的增长率和 f(n)的增长率相同，称作算法的渐进时间复杂度，简称为时间复杂度。其中 f(n)是问题规模 n的某个函数。

2.2.1计算方法：

1.用常数1取代函数中所有的常数

2.只保留最高项

3.最好情况时间复杂度：代码在最坏情况下执行的时间复杂度。

常用的时间复杂度所耗费的时间从小到大依次是

• O(1) < O(log n) < O(n) < O(nlog n) < O(n2) < O(n3) < O(n!) < O(nn)

2.2.2 一般法则

法则 1-----for循环

一次for循环的运行时间至多是该for循环内语句的运行时间X循环的次数。

for(i = 1 ; i <= n ; i++)
{
    x = x + 1;		/* 时间复杂度为O(n) */
}

法则 2-----嵌套的for循环

从里向外分析，在一组嵌套循环内部的一跳语句总的运行时间为该语句的运行时间X该组所有for循环的大小的乘积。

for( i = 0; i < n; i++)
{
    for(j = 0; j < n; j++)
        k++;		/* 时间复杂度为O(n*n) */
}

法则 3-----顺序语句

将各个语句的运行时间求和即可，其中的最大值即为运行时间。

for(i = 1 ; i <= n ; i++)
{
    x = x + 1;		/* 时间复杂度为O(n) */
}
for( i = 0; i < n; i++)
{
    for(j = 0; j < n; j++)
        k++;		/* 时间复杂度为O(n*n) */
}
/* 总时间复杂度为O(n*n) */

法则 4-----while语句

int count = 1;
while(count < n){
	count *= 2;
	/*时间复杂度为 O(1) 的程序步骤序列*/
}

/* 2^x = n  时间复杂度为O(log n) */

2.3 空间复杂度

算法的空间复杂度是通过计算算法所需的存储空间实现，算法空间复杂度的计算公式记作： S(n)=O(f(n))S(n)=O(f(n)) S(n) = O(f(n))S(n)=O(f(n)) 。其中，n 为问题的规模， f(n)f(n) f(n)f(n) 为语句关于 n 所占存储空间的函数。

2.4 递归：

int F(int x)
{
    if(x == 0)
        retuen 0;
    else 
        return 2 * F(x-1) + X * X;
}

1.它是否就是循环逻辑？

答案是：虽然函数会用到这个函数本身，但是我们并没有用函数本身来定义函数的一个特定的实例。即使用F（5）来得到F（5）的值才是循环，通过F（4）来得到F（5）的值不是循环的。

2.实现递归的基本准则：

基准情形：递归中必须要有某些基准情形，他们不用递归就能求解。

不断推进：对于那些需要递归求解的情形，递归调用必须总能朝着产生基准情形的方向推进。

设计法则：假设所有的递归调用都能运行。

合成效益法则：在求解一个问题的同一实例时，切勿在不同的递归调用中做重复性的工作。