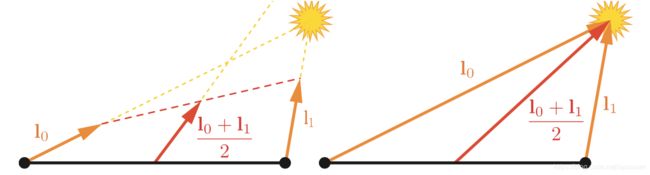
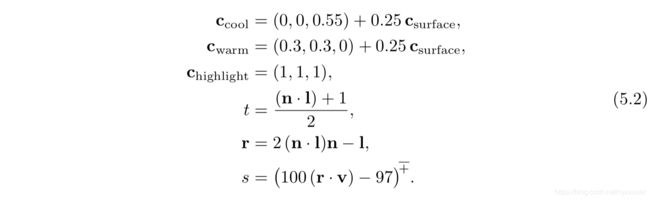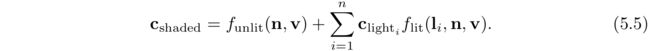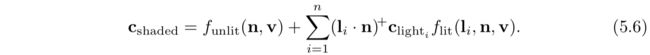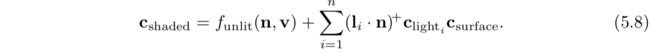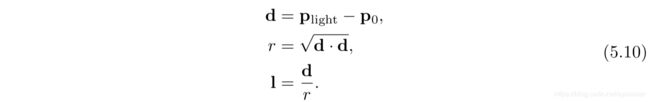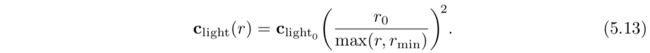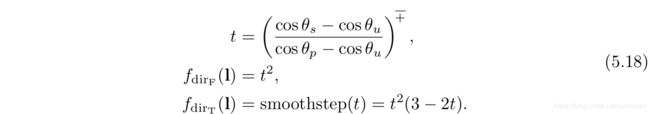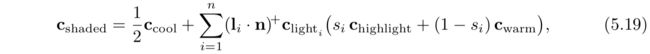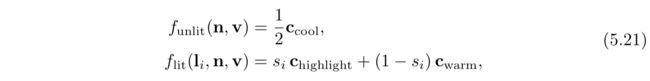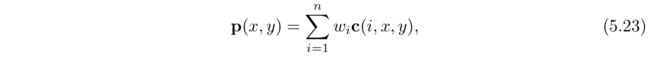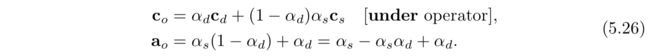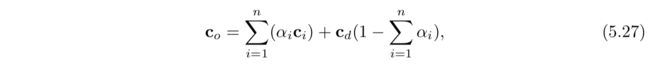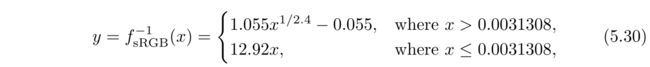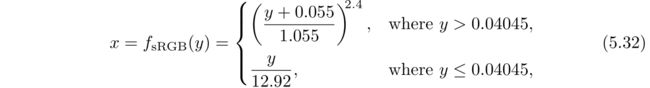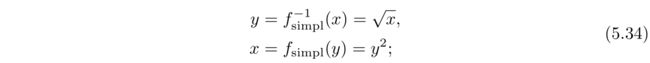《Real-Time Rendering 4th Edition》读书笔记--简单粗糙翻译 第五章 着色基础 Shading Basics

写在前面的话：因为英语不好，所以看得慢，所以还不如索性按自己的理解简单粗糙翻译一遍，就当是自己的读书笔记了。不对之处甚多，以后理解深刻了，英语好了再回来修改。相信花在本书上的时间和精力是值得的。

———————————————————————————————

”你需要做的是渲染出一张好图片“

        当你需要渲染一个三维对象时，模型不仅需要合适的几何形状，还需要有合适的视觉外观。根据应用程序的不同，其范围可以从照片写实（外观几乎和真实物体的照片一样）到出于创造而选择的各种风格化外观。如图5.1所示两种例子。

图 5.1  上图是用虚幻引擎渲染的写实山水场景。而下图的渲染用的是Campo Santo，这是专门用来渲染插图风格类型的。

5.1 着色模型（Shading Models）

        渲染一个物体外观的第一步是选择一个着色模型，用表面朝向，观察方向，光照等因素来决定物体的颜色。

 

        我们以Gooch着色模型（Gooch Shading model）的一个变种为例。这是第15章讨论的非真实感渲染的一种形式，Gooch着色模型旨在提高技术插图细节的清晰度。

 

        Gooch着色模型背后的基本思想是将表面的法线和光源的位置进行比较，如果法线指向光源，则使用暖色调为表面着色，相反则使用冷色调。介于两者之间角度则用插值。在这个例子中，我们添加了一种“高光（highlight）”效果来使物体外形具有光泽度。图5.2展示了Gooch着色模型的实际效果。

 

            

图 5.2 结合了Gooch着色模型和高光效果的风格化着色模型。上图展示了具有中性表面颜色的复杂模型，下图展示的是使用各种不同表面颜色的材质球。

 

        着色模型通常有可以控制外观变化的属性。渲染一个物体外观的第二步就是设置这些属性值。本例中，渲染模型只有一个属性，即表面颜色，如图5.2下图所示。

 

        和大部分着色模型一样，本例也受到相对于观察方向和光照方向的表面朝向的影响，出于着色目的，这些方向通常用归一化（单位长度）向量表示，如图5.3所示。

 

图 5.3 本例着色模型（其实大部分着色模型）的输入用单位向量表示，表面法线 n，观察向量 v，光照方向 l。

 

        现在我们已经定义好了着色模型的全部输入，接下来可以看下着色模型的数学定义：

在等式中，采用了以下一些中间计算：

        该定义中的一些数学表达式也经常在其他的着色模型中见到， Clamping操作在着色中经常用到，常见的是clamp到0或者clamp到0和1之间。在这里我们用1.2节所介绍的 符号来表示计算高光混合因子s需要clamp在0和1之间。点积运算符出现了三次，每次出现在两个单位向量之间，这是一种很常见的模式。两个向量的点积是它们的长度和它们之间夹角的余 弦的乘积。所以，单位向量的点积就是它们之间夹角的余 弦。由余 弦组成的简单函数通常是用来表达两个方向之间关系的 最准确也最好的 数学表达式，例如本例中的光方向和表面法线之间的关系。

        着色中另外一个常见操作是对颜色（ 在0和1之间 ）进行线性插值。这个操作采用 这种方式，在Ca和Cb之间进行插值，随着t从1到0变化，插值结果从Ca到Cb。这个模式在Gooch着色模型中出现了两次，第一次是在Cwarm和Ccool之间进行插值，第二次是将先前插值结果和Chighlight进行插值。线性插值在着色中出现频率很高，在着色语言中有内置函数，称为lerp或者mix。

 

         “ r = 2 ( n · l ) n − l ”是计算反射光向量，计算l关于n的反射。尽管不像上两个操作（clamp和lerp或mix）出现的那么频繁，但是一般着色语言中也有内置反射功能。

 

        通过将这些操作以不同的方式同各种数学表达式和着色参数值组合在一起，可以为多种风格化外观和写实外观定义着色模型。

 

5.2 光源（Light Sources）

        本例着色模型中光照的影响很简单，仅提供了一个主要方向。当然，在现实世界中光照很复杂，可以有多个光源，每个光源都有自己的尺寸，形状，颜色和强度，如果加入间接光照则会有更多变化。在第九章，基于物理的真实感着色模型需要考虑到所有这些参数。

 

        根据应用程序和视觉风格的需要，各种风格化的着色模型可以以多种不同方式使用光照。一些高度风格化的着色模型可能根本就没有光照概念，或仅仅用来提供一个简单的方向性（例如Gooch着色模型）。

 

        着色模型中光照的复杂性也反映在，以二进制形式对光的存在或不存在作出反应。着色模型在有光照的情况下会展示一种外观，在没有光照的情况下将具有不同的外观。这暗示了区分两种情况的一些标准：距光源的距离、阴影（第七章讲到）、表面是否背对光源（表面法线n和光线向量l之间的夹角大于90度）或这些因素的组合。

 

        从以二进制形式表示光的存在或不存在到光强度的连续范围都是一小步，可以用不存在和完全存在之间的简单插值表示，这表示对强度是一个有界范围，可以从0到1，或者表示为以某种方式影响着着色的无边界量。后者的常见操作是将着色模型分成有光照和无光照两部分，光强度Klight线性缩放有光照部分：

这可以容易拓展到一个RGB光颜色Clight，

和多光源，

        无光照部分funlit(n,v) 对应于将光视为二进制的着色模型的“不受光影响时的外观”。它可以有各种各样的形式，取决于所需要的视觉风格和应用程序所需。例如 funlit() =(0，0，0)将使不受光源影响的任意表面以纯黑色表示。当然，无照明部分也可以为无照明物体表达某种形式的外观，类似于Gooch着色模型的背向光源的冷色。通常着色模型表示有光照部分的光源并非直接来自某个明确放置的光源，例如来自天空的光或来自周围物体的反射光。这些光的形式将在第十章和第十一章讨论。

 

        前面提到的，如果光的方向和表面法线的夹角大于90度，则光源不会影响表面上的点，实际上是影响表面的背面。这可以看作是相对于表面的光方向和光对着色的影响之间关系的一个特例。尽管是基于物理的，这个关系可以从简单的几何原理派生而来，对许多非基于物理的着色模型和风格化着色模型很有用。

 

        可以将光作用于表面的效果可视化为一组射线，其中射线击中表面的密度对应于表面着色中的光强度。如图5.4所示，该图显示了一个光照表面的横截面。沿该横截面入射到表面的光线与表面的交点之间的距离与l和n之间的角度的余弦成反比。因此，入射到表面的光线的总密度与l和n之间角度的余弦成比例，正如前面说到的，等于两个单位向量的点积。在这里，可以看到为什么定义光向量的方向和光的传播方向相反了，否则我们不得不在点积运算之前对其进行取反。

 

图 5.4 上面一排展示的是光击中表面的横截面的示意图，左图的光线是垂直击中表面，中间图光线以一个倾角击中表面，右图展示的是用向量的点积来计算向量夹角的余弦。下图展示的是在表面上的某一个横截面。

 

        更准去的说，当点积为正时，光线密度和点积结果成正比，负值对应于从表面背面发出的光线，是无效的。因此在着色公式中，需要将点积保证大于0，用 来表示（1.2节中介绍），这意味着点积为负值则取零。则有：

        支持多光源的着色模型通常使用的是公式5.5（更通用）或公式5.6（需要基于物理的模型）。公式5.6对于一些风格化着色模型也有用，因为它可以帮助确保光照的整体一致性，特别是对于背离光源或处于阴影中的表面。当然也有一些并不是适用，而这些模型则可以使用公式5.5。

 

        函数flit()最简单的选择是使用一个常量颜色，

这样着色模型公式为：

        这个光照部分对应于 Lambertian着色模型，该模型工作在理想漫反射表面（即完全无光泽的表面）。Lambertain着色模型可以单独用于简单着色，它是许多着色模型的关键组成部分。

 

        从公式5.3到5.6可以看出，一个光源影响着色模型靠两个参数：指向光源的向量l和光颜色Clight。有多种不同类型的光源，它们的主要区别在于这两个参数在场景中的变化方式。

 

        接下来将讨论几种常见的光源，它们有一个共同点： 给定了一个表面位置后，每个光源仅从一个方向I照向表面。换句话说，从着色表面位置来看，每个光源都是一个无限小的点。对于现实世界中的光源，这并不严格对，但是大多数光源相对于它们到表面的距离都很小，因此这是一个合理的近似值。

 

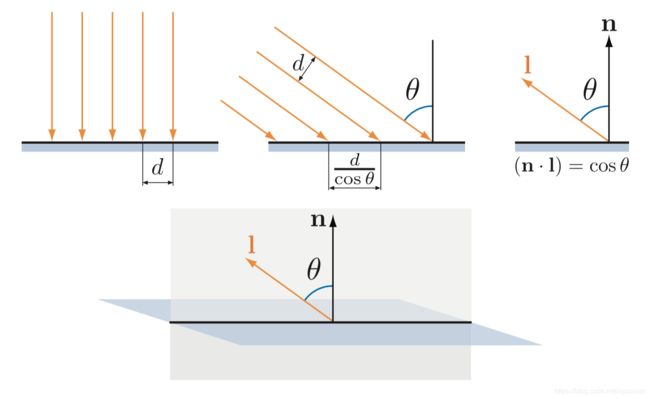
5.2.1 平行光（Directional Lights）

        平行光是光源中最简单的模型，在整个场景中I和Clight都是恒定的，除了Clight可能会被阴影影响而衰减。平行光没有位置，当然，实际光源在空间中有一个特定的位置，平行光是抽象的，当光源到场景的距离相对于场景的大小非常大的时候，平行光会表现很好。例如，一个20英尺远的泛光灯可以照亮一个小的桌面西洋镜，则灯可以看作是一个平行光。另外一个例子是凡是被太阳照到的场景，除非所涉及的场景是诸如太阳系内行星之类的东西。

 

        平行光的概念可以稍微扩展下，在允许光方向I不变的情况下，可以改变Clight的值。这通常发生在把光照效果和场景的特定部分绑定的时候，一般是为了表现一些特别效果。例如，有两个嵌套（一个在另外一个内）的立方体盒子，在外部盒子的外部的Clight是（0，0，0），纯黑色，而在内部盒子的内部Clight是某个常量。而在两个盒子之间的采用的是平滑插值得到的结果。

 

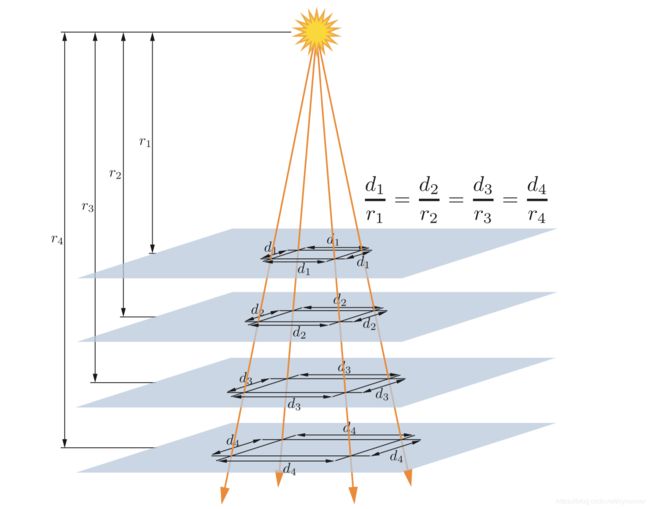
5.2.2 精准光源（Punctual Lights ）

        精准光源（Punctual Light）并没有准时的意思（punctual是准时的意思），而是一个具有位置的光照，和平行光不同。和现实中的光不同，这类光没有尺寸，没有形状没有大小。使用术语“Punctual”，是因为在拉丁语中punctus 表示“点，point”。用术语“point light”（点光源）来表示一种特定的发射器， 它可在所有方向上均等的发射光线。 因此点光源和聚光灯（spotlight）是精准光源的两种不同表现形式。光线向量I取决于当前着色表面上的点P0和精准光源Plight：

        这个方程是一个向量归一化示例：将向量除以其长度即可产生指向相同方向的单位长度的向量。这也是一个常见的着色操作，在大部分着色语言中都有内置函数。但是，有时候需要这个操作的中间结果，这需要多个步骤，并且要显示执行归一化。

所以有：

        我们需要的中间值是r，即精准光源和当前着色表面上的点之间的距离。除了将其用于归一化光向量外，还需要r的值来计算光颜色Clight随着距离的衰减变化（变暗）。这将在下一节讨论到。

 

点光源/泛光源 （Point/Omni Lights）

        在所有方向上均匀发射光线的精准光源，称为点光源（Point Lights）或泛光源（Omni Lights）。对点光源，Clight值随着r的增大而衰减。图5.5展示了为什么会衰减，利用了类似于图5.4中的余弦因子进行几何推理。在给定的表面上，来自点光源的光线间的距离和从表面到光源的距离成正比。与图5.4中的余弦因子不同，此间距的增加沿着表面两个维度发生，因此射线密度（及因此引起的光颜色Clight值）与 成正比。这样一来，r就是计算Clight的唯一因素，其中 定义为Clight在固定距离r0处的值：

公式5.11通常被称为 平方反比光衰减（inverse-square light attenuation）。尽管从技术上讲，对点光源是有着正确的距离衰减。但是还有一些问题让这个方程并不适合于实际的着色使用。

 

图5.5 点光源发出的光线间的间距与距离r成比例增加，因为光线间的间距同时在二维上增加，因此光线的密度（及光强）和r的平方的反比成正比。

 

        第一个问题发生在相对较小的距离处，随着r趋向于0，Clight的值会增加到无限大，随着r为0时，将得到一个除以0的奇点，为了解决这个问题，一种常见的做法是在分母增加一个小值ε：

ε的确切值取决应用程序， 例如，在虚幻引擎中使用的 ε=1cm。

 

        另外一种方案是（CryEngine和Frostbite 游戏引擎采用的）是把r钳位到一个最小值 rmin ：

和前面采用ε的方法不同， r min   有物理解释：发光物体的半径。对于小于rmin 的r值所对应的是穿透物理光源内部的着色表面，这是不可能的。

 

        相反的，平方反比衰减的第二个问题发生在相对较大的距离处。这个问题不在于视觉效果而在于性能。尽管光强随着距离增加而不断减小，但是永远都到达不了0。为了高效渲染，希望光在某个有限距离处光强为0。这里有许多不同的方法来修改平方反比方程来实现这一目的。理想情况下，修改应该尽可能少的更改。 为了避免在光线影响范围边缘出现明显的截止，建议修改后的函数和该函数的导数在同一距离处值为0。一种解决方案是对平方反比方程乘以 窗口函数（ windowing function ）。虚幻引擎和Frostbite游戏引擎采用的是：

+意味着钳住该值，2则意味着进行平方，如果最外层括弧里的值是负数，则取0，然后进行平方，值仍为0。图5.6展示了一个平方反比曲线的例子。

 

图 5.6 展示了平方反比曲线（利用 ε方法来避免出现除0的情况， ε =1 ），窗口函数曲线（采用的是公式5.14所示，其中 r max 设为3）以及两者结合在一起的曲线。

 

        应用需求将会影响到所用方法的选择。当距离衰减函数在以相对较低的空间频率进行采样时（例如在光照贴图或逐顶点），r=rmax时的导数为0特别重要。CryEngine并不使用光照贴图和顶点光照，所以它采用一个更简单的调整，在0.8rmax到rmax间采用线性衰减。

        对一些应用，匹配平方反比曲线并不是优先事项，因此使用了一些其他的功能。可有效的将公式5.11-5.14概括为：

其中 f dist ( r )是距离函数，这类函数称为 距离衰减函数（distance falloff functions）。在一些例子里，采用非平方反比衰减函数是处于性能考虑。例如，游戏Just Cause 2 的光线需要非常便宜的计算方式，规定了一个衰减函数，很容易计算，同时也足够平滑来避免逐顶点带来的瑕疵：

       

       而在一些例子里，衰减函数的选择是出于风格创造性的考虑。例如，在虚幻引擎中，同时可以做写实类和风格化游戏，所以拥有两种光照衰减模型：一种是平方反比模型，如公式5.12所示，另外一种是指数衰减模型，可以调整来创建各种衰减曲线，游戏Tomb Raider的开发人员采用了样条编辑工具来编写衰减曲线，从而可以更好地控制曲线形状。

 

聚光灯（Spotlights）

        跟点光源不同，几乎现实世界中所有光源的光照都随着方向发生变化，和距离一样。可以用 方向衰减函数 f dir ( l )表示，和距离衰减函数一起来定义光强度的整体空间变化：

       选择不同的fdir(l)，可以产生不同的光照效果。一种很重要的效果就是聚光灯，将光投射到圆锥形中。聚光灯的方向衰减函数具有围绕聚光灯方向向量s的旋转对称性，可以由s和到表面的反向光向量-l之间角度θs 表示。光向量需要反转，因为定义l为由表面指向光源，而在这里需要指向远离光的向量。

 

        大部分聚光灯用θs 的余弦来表示，聚光灯通常由一个 阴影角（umbra angle） θ u ，定义了光的边界fdir(l) = 0 ，θs ≥ θu 。这个阴影角和距离衰减中的rmax 类似，有着剔除作用。聚光灯还有一个 半阴影角（penumbra angle） θ p，它定义了一个内部圆锥体，而在这个内部圆锥体内光强度是最大值（无衰减）。如图5.7所示。

 

图 5.7 聚光灯示例图。 θ s 是s和-l之间的夹角， θ p 是 半阴影角， θ u 是阴影角。

 

        聚光灯虽然有各种方向衰减函数，但是都类似。例如Frostbite游戏引擎的衰减函数 fdirF (l)以及在浏览器图形库three.js中用到的衰减函数 fdirF (l)。

其中 smoothstep函数是一个三次多项式的平滑步长函数，在着色的平滑插值中经常看到。在大部分着色语言中都有内置函数。

       

       图5.8展示了目前为止我们讨论的光源。

 

图5.8 光源类型，从左到右依次是平行光，无衰减的点光源，平滑过渡的聚光灯。注意，由于光线和平面的角度变化，点光源朝着边缘变暗。

 

        fdir(l)函数不限于上面讨论的简单的聚光灯的衰减函数，它可以代表任何类型的方向变化，包括真实世界光源的复杂列表模式测量。 IES（Illuminating Engineering Society）以及为这类测量定义了一份标准文件格式。

 

5.2.3 其他光源类型

        平行光和精准光源的主要特征是如何计算光方向I。而其他类型的光源的光方向也有对应的计算方法。例如，古墓丽影（Tomb Raider）不仅用到了上面讨论的光源类型，还 使用了一种以线段代替点的光源，胶囊光源。对每个需要着色的像素，以指向线段最近点的方向作为光方向l。

 

        目前为止讨论的光源都是抽象的，在现实中，光源上有大小和形状的，并且它们从多个方向照亮平面上的点。在渲染中，这类型的光源称为 区域光源（area lights），在实时渲染应用程序中，它们的使用率正稳步增长。区域光源渲染技术分为两类：模拟因区域光源被部分遮挡而阴影边缘需变软的情况，以及模拟区域光源对表面着色的影响。第二种对光滑像镜子的表面最为明显，在这种表面，可以通过反射看清光源的形状和大小。平行光和精准光源不大可能被废弃，尽管它们不再像以前那样普遍使用。随着对光的面积的近似计算的发展，并且实现起来相对简单，肯定会得到广泛使用。随着GPU性能的提高，允许使用比以前更为复杂的技术。

 

5.3 实现着色模型（Implementing Shading Models）

        为了使用，这些着色方程和光照方程当然需要用代码实现。

 

5.3.1 求值频率（Frequency of Evaluation）

        在设计一个着色的实现时，计算需要根据求值频率来划分。首先，确定给定的计算结果是否在整个DrawCall过程中保持不变。在这种情况下，计算通常在CPU上执行，因为GPU的计算着色器通常用来做一些昂贵的计算。计算结果由uniform着色器输入传给图形API。

        即使在这一类别中，也存在各种可能的求值频率。最简单的情况是就是着色方程中的常量子表达式，但这只能应用到基于很少更改因素的计算中，例如硬件配置和安装选项。编译着色器时可以解决这种着色计算，在这种情况下，甚至不需要设置uniform着色器输入。 或者，可以在安装时或加载应用程序时在脱机的预计算过程中执行计算。

        另外一种情况是，当着色计算结果在应用程序运行过程中发生变化，但速度很慢，可以不必每帧都进行更新。例如，光照因素取决于虚拟世界中一天的时间。如果计算很昂贵，可以尝试在多帧执行一次。

        其他的情况，包括每帧执行一次的计算，例如组合观察矩阵和透视矩阵；也包括每个模型执行一次的计算，例如，根据模型位置更新模型的光照参数；或者每一次Draw Call执行一次的计算，例如更新模型中每种材质球的参数。利用求值频率将uniform着色器输入分组有助于提高应用程序的效率，并且通过最小化更新频率来提高GPU性能。

        如果着色计算结果需一次DrawCall改变一次，则不能通过uniform着色器输入传输给着色器，取而代之，它必须由第三章描述的可编程阶段之一进行计算，并且如果需要，可由varying 着色器输入传递给其他阶段。理论上讲，可编程阶段都可以进行着色计算，每个阶段对应不同的求值频率：

        顶点着色（Vertex Shader）— 每个细分前的顶点（Evaluation per pre-tessellation vertex）求值。

        壳着色（Hull Shader）— 每个表面Patch点求值。

        域着色（Domain Shader）— 每个细分后的顶点求值。

        几何着色（Geometry Shader） — 每个图元求值。

        像素着色（Pixel Shader） — 每个像素求值。

        实际上，大部分着色计算都是针对每个像素执行的。尽管这些通常在像素着色器中实现，但如今计算着色器已经越来越普遍了。其他阶段主要用的是几何运算，例如变换和变形。

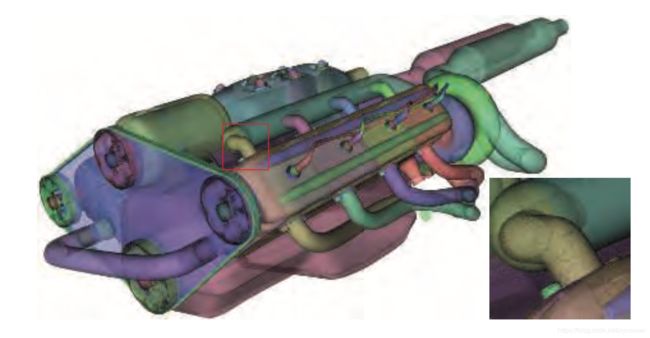
        图5.9展示了具有广泛顶点密度的模型的逐顶点和逐像素的着色结果。对龙来说，模型网格很致密，两者的差异很小。对茶壶而言，顶点着色求值会导致可见的错误，例如棱角分明的高光，而且在两个三角形平面上的顶点着色效果明显不对。这些错误的原因是，着色方程中某些部分的值在网格表面呈非线性变化，尤其是高光部分。这使得它们不适合顶点着色，因为顶点着色的结果在传递给像素着色之前需要在三角形上线性插值。

图 5.9 左列显示的是逐像素的评估结果，中间列显示的是逐顶点评估结果，右侧列显示的是每个模型的线框渲染，以展示顶点密度。

        原则上讲，可以在像素着色中仅计算镜面高光部分，其余部分在顶点着色中进行。这可能不会造成视觉瑕疵，并且理论上还可以节省一些计算。实际上，这种混合实施方案并不是最佳。着色模型中线性变化部分的计算通常花费最少，并且以这种方式拆分开来计算往往会增加足够的开销，例如重复的计算和额外输入，弊大于利。

        正如前面所说，在大多数顶点着色的实现中，顶点着色负责着非上色操作，例如几何变换和变形。最终生成的几何表面属性，转换到合适的坐标系中，有顶点着色写出，在三角形上线性插值，最终作为varying着色器输入传递给像素着色阶段。这些属性包括表面位置、表面法线，如果需要法线贴图，还可以选择表面切线向量。

        注意，尽管顶点着色一直生成单位长度的表面法线，但是插值会改变其长度。如图5.10左图所示。因为这个原因，在像素着色阶段法线需要进行归一化操作。但是顶点着色生成的法线长度还是很重要，如果各顶点之间的法线长度差异很大，例如，作为顶点混合的副作用，会导致插值倾斜，如图5.10右图所示。由于这两种情况，在顶点着色和像素着色中，在实现插值之前和实现插值之后都会对插值向量进行归一化操作。

图 5.10  左图可以看到单位法线经过表面插值后会生成长度小于1的插值向量。右图可以看到两个明显长度不一的表面法线经过插值后会发现插值方向偏向于较长法线的方向。

        和表面法线不同，一些指向特定位置的向量，例如观察方向和精准光源的光方向，通常不会进行插值。取而代之的是，在像素着色中用插值表面位置来计算这些向量。在像素着色中除了在任何情况下都要进行归一化操作外，这些向量都是通过向量减法得到，因为快。如果出于某个原因，需要插值这些向量，请不要事先对其进行归一化，会导致不正确的结果，如图5.11所示。

图 5.11 对两个光向量进行插值。左图，对插值之前进行了归一化操作，插值后会不正确。右图，插值之前没进行归一化操作，结果正确。

        前面提到顶点着色会把表面几何转换到“适当的坐标系”内，通过uniform变量把摄像机和光源的位置传递给像素着色中，就是常见由应用程序转换到相同坐标系的例子。这样会最大化减少像素着色中把所有着色模型向量带入同一坐标空间中。但是哪个坐标系是合适的坐标系？可能是全局世界坐标系，或摄像机的局部坐标系，或更为罕见的当前渲染模型的局部坐标系。通常由渲染系统作出选择，基于系统性能表现，例如灵活性和简单性。例如，如果需要渲染的场景中有大量的光源，那么或许选择世界空间是个很好的选择，这样可以避免大量光源位置的变换。或者，最好的选择是选择摄像机空间，为了更好的优化和观察向量有关的像素着色操作，并尽可能提高精度。

        尽管大部分着色实现包括即将要讨论的示例的实现，都遵循上述概述。当然也有些例外，一些应用出于风格化原因，选择了多面外观的逐图元的着色求值，这种风格通常被称为平面着色（Flat Shading）。如图5.12所示两个例子。

图 5.12 选择了平面着色（Flat Shading）作为风格的两款游戏：Kentucky Route Zero，上图， That Dragon， Cancer 下图。

        原则上，平面着色可以在几何着色中执行，但目前都是在顶点着色中实现。这和关联每个图元的属性及其第一个顶点，并禁用顶点值插值来完成。禁用插值（可由每个顶点值分别完成）会使第一个顶点的值传递给图元中所有的像素。

5.3.2  实施案例

        接下里会展示一个着色模型实现的案例。如前面所述，即将实现的着色模型和公式5.1中拓展Gooch模型类似，但经过修改可与多个光源一起使用。公式为：

中间计算有：

该公式适合公式5.6的多光源结构，为了方便，此处重复展示下：

其中：

        在大部分渲染应用程序中，材质属性，例如Csurface，的变化值将会存储在顶点数据中，或更为常见的纹理中。但是为了简单起见，在该示例中假设Csurface在整个模型中都是不变的。

 

        在示例实现中将会利用着色器的动态分支功能遍历所有光源。虽然这种方法在场景相当简单的情况下可以很好工作，但在多光源的大场景或多光源的几何复杂的场景中，无法很好地缩放。为了简单起见，仅支持一种光源：点光源。尽管实现很简单，但它遵循了前天介绍的最佳实践。

 

        着色模型并不是孤立实现的，而是在一个更大的渲染框架的上下文中实现的。该示例在一个简单的WebGL 2应用程序中实现的，但相同的原理也适用于复杂的框架。

 

        接下来会讨论一些GLSL着色代码和应用程序的调用JS WebGL的一些示例。目的不是讲述WebGL API的细节，而是展示一般的实现原理。通过由内而外的顺序贯穿实现过程，从像素着色开始，然后到顶点着色，最后到应用程序对图形API的调用。

 

        如3.3节所说，使用GLSL术语，着色器输入分两类。 一种是Uniform输入，这些输入由应用程序设置的值，并且在一次DrawCall期间保持不变。第二种是varying输入，这些输入值可以在着色器间调用的时候改变。在这可以看到像素着色器的varying输入的定义，在GLSL中标志为in，同理输出为out：

in vec3 vPos;
in vec3 vNormal;
out vec4 outColor;

 

        像素着色只有一个输出，就是最终着色颜色。像素着色的输入和顶点着色的输出相匹配，在传递给像素着色之前经过了在三角形上进行插值。像素着色由两个varying输入：表面位置和表面法线，都是在世界空间坐标系内的。而uniform输入的数量要大得多，为了简洁，这里只定义了两个和光源有关的输入：

struct Light { 
    vec4 position;
    vec4 color; 
};
uniform LightUBlock {
    Light uLights[MAXLIGHTS];
};
uniform uint uLightCount;

因为这里都是点光源，所以定义光源的结构体里有一个position和一个color。这里用的是vec4而不是vec3是为了符合GLSL std140数据分布标准。在这个例子中，尽管std140分布会导致一些空间浪费，它简化了确保CPU和GPU之间数据分布需一致的任务，这就是为什么这里采用std140的原因。Light 结构体的数组被定义成一个uniform块，这是GLSL的特色，因为把一组uniform变量绑定到一个缓冲对象中会让数据传输很快。数组的长度就是应用程序允许一次drawcall中最大的光源数量。后面也会看到，shader源代码在编译之前，会用MAXLIGHTS宏来表示这一数量，本例中是10。uniform整数uLightCount表示的是实际在一次drawcall中激活的光源数。

        接下来，看一看像素着色代码：

vec3 lit(vec3 l, vec3 n, vec3 v) {
    vec3 r_l = reflect(-l, n);
    float s = clamp(100.0 * dot(r_l, v) - 97.0, 0.0, 1.0);
    vec3 highlightColor = vec3(2,2,2);
    return mix(uWarmColor , highlightColor , s);
}
void main () {
    vec3 n = normalize(vNormal);
    vec3 v = normalize(uEyePosition.xyz - vPos);
    outColor = vec4(uFUnlit , 1.0);
    for (uint i = 0u; i < uLightCount; i++) {
        vec3 l = normalize(uLights[i].position.xyz - vPos); 
        float NdL = clamp(dot(n, l), 0.0, 1.0);
        outColor.rgb += NdL * uLights[i].color.rgb * lit(l,n,v);
    }
 }

        我们定义了一个lit（）函数，被main（）函数调用。总体来说，这就是公式5.20和5.21以GLSL来实现的。注意Funlit（）的值和Cwarm值都是以uniform变量的形式传入的。因为这些值都是在整个drawcall中保持不变的，可以由应用程序计算这些值，以来节省一些GPU周期。

        像素着色使用了一些GLSL内置函数，reflect（）函数的两个参数是光向量和表面法线。我们希望光向量和反射向量都是背离表面的，所以传入的reflect（）的参数是-l。clamp（）函数有三个参数，在大部分GPU上，钳制到0 和1（与HLSL saturate（）函数相对应）之间的范围是最为快速的，可以被GPU快速解释。这也是为什么在这里用0和1，尽管我们只需要限制大于0，而且知道它永远不会超过1。mix（）函数同样有三个参数，以第三个参数为因子（0到1之间）对前两个参数进行插值， 本例中插值的是暖颜色值和高光颜色值，在HLSL中对应的函数为lerp（），意思是线性插值。最后，normalize（）函数是将一个向量除以它的长度，缩放长度为1。

layout(location=0) in vec4 position;
layout(location=1) in vec4 normal; 
out vec3 vPos;
out vec3 vNormal;

        接下来看下顶点着色代码，将不会展示任何它的uniform输入了，但是会展示varying输入和varying输出的定义：

注意，前面讲到顶点着色的输出对应像素着色的输入，这些输入包括了 指定数据如何在顶点数组中布置的指令。顶点着色的主代码如下：

void  main（）{
    vec4 worldPosition = uModel * position;
    vPos = worldPosition.xyz;
    vNormal = (uModel * normal).xyz; 
    gl_Position = viewProj * worldPosition;
}

这些都是常规操作，把表面位置和表面法线转换到世界空间，然后传递给像素着色用，最后把表面位置转换到裁剪空间，赋值给gl_Position，这是一个系统定义的变量，是任何顶点着色都需要输出的一个变量，光栅化会用到。

        注意，在顶点着色中法向量并没有归一化，法向量并不要归一化，因为在原始网格数据中它们的长度就是1，应用程序不会做任何不均匀改变其长度的操作，例如顶点混合或非均匀缩放。模型矩阵有一个统一缩放因子，会成比例改变所有的法线长度，因此不会导致出现图5.10右图所示的问题。

 

        应用程序利用WebGL API对各种渲染和着色进行设置。每个可编程着色阶段都是独立设置的，然后把将它们都绑定到对应程序对象。像素着色设置代码如下：

var fSource = document.getElementById("fragment").text.trim(); 
var maxLights = 10;
fSource = fSource.replace(/MAXLIGHTS/g, maxLights.toString());
var fragmentShader = gl.createShader(gl.FRAGMENT_SHADER); 
gl.shaderSource(fragmentShader , fSource); 
gl.compileShader(fragmentShader); 

注意“片元着色，fragment shader”对应着像素着色。MAXLIGHTS的赋值也在这，大部分渲染框架都执行类似的预编译着色操作。

        还有更多的应用程序端代码用于设置uniform变量，初始化顶点数组，清除绘制等等，可以在API指南中看到。我们的目的是通过自身的编译环境了解着色器是如何视为单独的处理器。 

 

5.3.3 材质系统（Material System）

        很少渲染框架只是简单一个着色器，通常，需要一个专门的系统来处理各种材质，着色模型及着色器。

        前面章节有说到，一个着色器可以认为是一段程序，在GPU可编程着色阶段触发。因此，它是低级图形API资源，而不是艺术家直接交互的对象。相反，材质是面向艺术家的表面视觉外观的封装。材质有时候也描述非视觉外观方面，例如碰撞属性，不在本书讨论范围内。

        虽然材质是通过着色器来实现的，但不是简单的一对一对应关系。在不同的渲染情况下，相同的材质可能使用不同的着色器。一个着色器可被多个材质使用。最常见的例子是参数化材质，以最简单的形式，材质参数化要求两种类型的材质实体：材质模板和材质实例。每个材质模板都是描述了一个类型的材质，具有一组参数，根据参数类型可以分配数字，颜色或纹理贴图。每个材质实例对应一个材质模板和一组特定的参数值。一些渲染框架，像虚幻引擎，允许更复杂，层次结构，材质模板可以从其他模板派生。

        参数可在应用程序运行时解析到，通过uniform输入传递给着色程序，或者在着色程序编译时通过某些宏替换得到参数。一种常见的编译时参数是一种布尔开关，它控制着是否激活材质的特定特征。

        尽管材质参数可能和着色模型的参数是一一对应关系，但是并非总是如此。材质可能将某个着色模型参数的值，例如表面颜色，固定为恒定值。或者，着色模型参数也可以由一系列复杂操作的结果计算得到。在某些情况下，像表面位置，表面朝向甚至时间之类的参数都可能会影响参数的计算。着色基于表面位置和朝向在地形材质很常见。例如，高度和表面法线可以被用来控制降雪效果。着色基于时间在动画材质中很常见，例如闪烁的霓虹灯。

        材质系统最重要的任务之一就是将各种着色器功能划分为单独的元素，并控制这些元素的组合方式。在许多情况下，这种类型的组合很有用，包括以下几种：

        ·使用几何处理（例如刚体变换，顶点混合，变形，曲面细分，实例化及裁剪）来构成表面着色。这些功能变化独立：表面着色基于材质，几何处理基于网格，因此，很方便按需进行组合。

        ·用类似于像素丢弃和像素混合的合成操作来构成表面着色。这和移动GPU尤其相关，在移动GPU中，混合是像素着色中常见操作。

        ·将计算着色模型参数的操作和着色模型自身的计算组合在一起。这可以只需实现一次着色模型，然后计算结果就可用于计算各种着色模型参数。

        ·按材质特征选择。这样可分别编写每个功能的实现。

        ·将着色模型和模型在光源评估中的参数计算（计算Clight和光向量l）进行组合。技术，像延迟渲染，会改变组合的结构。支持多种这类技术的渲染框架又多了一层额外的复杂性。

        如果图形API提供来这类着色代码模块化的话，将会很方便。不幸的是，不像CPU代码，GPU代码不能对代码块进行编译后链接。每个着色阶段的程序都作为一个单元进行编译。着色阶段之间的分隔有着有限的模块性，在某种程度上适合列表中的第一项：使用几何处理来构成表面着色。但拟合效果并不理想，因为每个着色器同时也需要处理其他的操作，并且其他类型的合成仍需处理。考虑到这些限制，唯一让材质系统能够实现全部类型的合成的方法就是源码级别（source-code level）。这主要涉及到连接和替换，通常用C风格的预处理指令（例如#include，#if，#define）执行。

        早期的渲染系统具有相对较少的着色变动，并且通常都是手动编写的。这有一些好处，例如，可以方便优化变动。但是，随着变动数量的增多，这种方法变得不切实际了。当考虑到所有不同的部分和选项时，变动数量会很庞大。这也就是为什么模块化和可组合性如此重要的原因。

        设计处理着色器变动系统需要解决的第一个问题是，为了表现不同的效果，是选择在运行时使用动态分支还是选择在编译时使用条件预处理。在较老的硬件是不支持动态分支或非常缓慢，因此运行时选择不是一个好选择。所有的变动都会在编译时进行处理，包括不同类型光源的所有可能组合。

        相反，现代GPU可以很好地处理动态分支，尤其在一次DrawCall中所有的像素分支相同时。如今，许多功能变化（例如光源数量）都是运行时处理。然而，给着色器添加大量功能变化会带来不同的成本：寄存器数量的增加和占用率的相对减少。因此编译时的处理变化仍然很重要，它会避免一些复杂逻辑。

        现代材质系统同时使用了实时运行和编译时的着色变动。即使不在编译时处理全部工作，但随着总体复杂性和变动数量在增加，因此仍然需要在编译时处理着色变动。

        材质系统设计时有一些策略：

        ·代码复用（Code reuse ） 在共享文件中实现功能，用#include指令来访问这些功能。

        ·减法（Subtractive ） 利用组合编译时预处理条件和动态分支来删除不需要的部分以及对互斥的备选方案间进行切换。

        ·加法（Additive ） 各种功能都被定义成拥有输入连机器和输出连接器的节点，并且可以组合在一起。这和代码重用类似，但结构更清晰。节点之间的组合可以通过文本或可视化图形编辑器来完成。后者是为了让非技术人员更容易创造新的材质模版。通常可视化图形编辑只能访问着色器的一部分，例如虚幻引擎的图形编辑器智能影响着色模型输入的计算，如图5.13所示。

        ·基于模版（Template-based ） 接口被定义为只需要符合接口条就可以插入到不同的实现中。这比加法策略更加正式，通常用于较大的功能模块。常见的例子是分离着色模型参数的计算和着色模型自身的计算。

    图 5.13 虚幻引擎的材质编辑器。

        除了组合，还有一些其他的重要设计策略对现代材质系统需要考虑，例如需要在支持多平台的情况下最小复制着色代码。考虑到平台不同，着色语言不同，API不同，需要考虑的东西很多。迪斯尼的着色系统是一个很好的代表来解决这个问题，它使用专门的预处理层来处理用自定义着色语言写的着色程序。这就使得材质的编写和平台无关，可以自动翻译成对应平台的着色语言及实现。

        材质系统还需要有良好的性能。除了对着色变动进行专门的编译外，材质系统还有一些其他常见的优化。迪斯尼着色系统和虚幻引擎会自动检测在一次DrawCall中保持不变的计算（例如前面提到的冷色值计算和暧色值计算），并将其移到着色器之外。另外一个示例是迪斯尼中使用的范围界定系统，用以区分不同频率更新的常量（例如，逐帧，逐光照，逐对象），在适当的时间更新每组常量，可以减少API的开销。

5.4 锯齿和抗锯齿（Aliasing and AntiAliasing）

        想象一下，一个大的黑色三角形在白色背景上缓慢移动，由于屏幕网格单元被三角形覆盖，代表该单元的像素值的强度应该平稳下降。在大部分基本着色器中，一旦网格单元中心被覆盖，则像素会立马从白色变成黑色。标准的GPU渲染也不例外。可参阅图5.14最左列。

        用像素呈现三角形，边缘呈现锯齿状，因此这种视觉瑕疵会被称为“锯齿”，更正式讲，应该称为走样（aliasing），而为避免这个问题所用技术称为反走样技术（antialiasing）。

图5.14 上面一行的三幅图展示了三角形、直线和点的不同等级的反走样。下面一排是上面一排的放大版。最左列的每次采样使用的都是一个像素，这意味着没有使用反走样。中间列每个像素有四次采样，而右侧列每个像素有八次采样。

5.4.1 采样和滤波理论

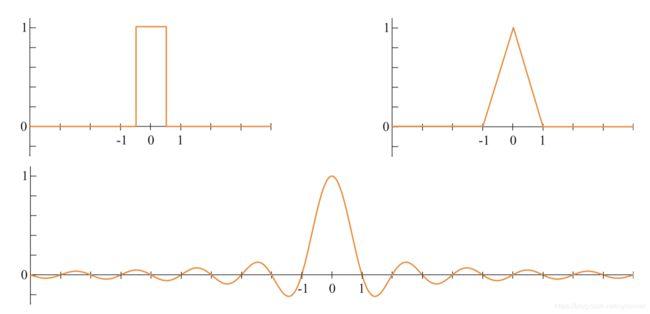
        渲染图像的过程本质上是一个采样任务。图像的生成色对三维场景进行采样的过程以给图中每个像素附上颜色。为了使用纹理映射，纹素需要重新采样才能在不同条件下有良好的效果。为了在动画中生成一组图像，通常以恒定的时间间隔对动画进行采样。

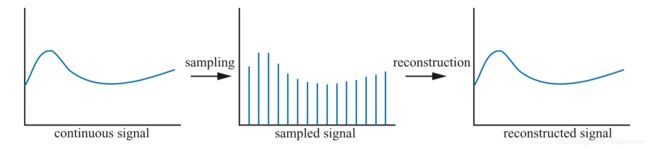
        图5.15展示了如何对连续信号以均匀间隔进行采样，即离散化。采样的目的是为了让信息数字化。这么做可以减少信息量，但是采样后的信号需要重构来恢复原始信号，这是采样对信号进行滤波完成的。

图5.15 左图是连续信号，中间图是采样后信号，通过对采样信号重构后可恢复成原始信号，见右图。

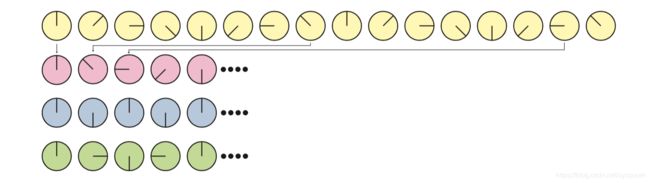
        当采样完成后，走样就可能出现。这是一个并不想要的瑕疵，需要对抗走样的发生。在古老的西方人看来，一个经典的例子就是用电影摄像机拍摄旋转木马的车轮。辐条移动速度如果比摄像机拍摄图像的速度快得多，轮子看起来似乎在缓慢旋转，甚至看起来没有旋转。如图5.16所示。之所以会出现这种情况，是因为轮子的旋转被拍摄进图像中需要花费一定的时间，被称为时间域走样（temporal aliasing）。

图5.16 最上面一排是车轮的辐条（或者说是原始信号）。第二排的采样不足，看起来车轮上朝相反的方向移动，这是采样频率太低的原因导致的走样。第三排中，采样率正好是每转一轮采样两次，因此无法确定轮子是朝哪个方向旋转，这就是Nyquist极限。在第四排中，采样率每转一轮要多两次采样（是Nyquis极限的两倍，4次采样），就可以看到轮子转动的正确方向。

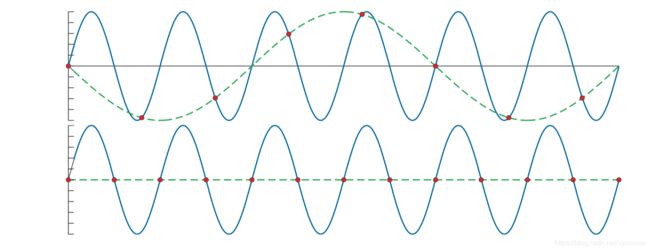
        计算机图像中经常出现的走样是光栅化一个线或三角形时出现的锯齿。当一个信号被采样的频率太低时会发生走样，如图5.17所示。为了正确的采样，采样率必须要大于需要采样的信号的最大频率的两倍。这被称为采样定理，采样率被称为Nyquist速率或Nyquist极限。Nyquist极限如图5.16所示。该定理使用的术语“最大频率”意味着该信号受到频带限制。换句话说，信号必须要相对于相邻两个样本之间的间隔足够平滑。

图 5.17 蓝色实线表示的是原始信号，红色圆点表示的是均匀间隔的采样点，绿色虚线表示的是重构后的信号。上图展示了采样率太低，导致重构后的信号的频率较原始信号的频率低太多，这时候出现了走样。而下图展示了采样率正好是原始信号的频率的两倍，重构后的信号就是一条水平线，证明了如果采样率再稍微增加点，则完美重构出原始信号成为可能。

        使用点采样三维场景时，是不会限制带宽的。三角形边缘，阴影的边界和其他现象会产生不连续的信号，则会有趋于无限的频率出现。无论对物体进行多紧密的采样，都会有小到无法采样的地方。因此，使用点采样来渲染场景是无法避免走样问题，但是我们几乎总是使用点采样。但是，有时会知道信号是受到带宽限制。例如，将纹理应用于表面时，可以通过像素的采样率计算出纹理采样的频率，如果此频率低于Nyquist极限，则无需采取任何特殊措施就可以得到正确的纹理采样。如果频率过高，则可使用多种算法对纹理进行宽带限制。

重构（Reconstruction）

        给定一个宽带限制的采样信号，我们将讨论如何从采样信号重构出原始信号，为此，必须要使用滤波器。图5.18展示了三种常用的滤波器。注意， 滤波器的面积应始终为1，否则重构的原始信号会出现增长或收缩。

 

图 5.18 左上图展示的是 盒式滤波（box filter） ，右上图展示的是 帐篷式过滤（tent filter） ，底图展示的是 sinc滤波（sinc filter）

 

        图5.19中， 盒式滤波（box filter）被用来重建采样信号，这是最差的滤波，因为生成的信号不是连续的阶梯，尽管如此，它还是经常在计算机图形学中被使用，因为够简单。从图中可以看出，每个采样点换成合适滤波，然后缩放，使滤波的最高点和采样点重合，这样经过重构后的信号就如右图所示。

 

图 5.19 利用盒式滤波重构出原始信号。

 

        盒式滤波可以被其他滤波取代。如图5.20所示， 帐篷式滤波（tent filter），又称三角形滤波（triangle filter），被用来重建采样信号。注意这个滤波实现了在相邻采样点进行线性插值，要优于盒式滤波，重建后的信号是连续信号了。

 

图 5.20 利用帐篷式滤波重构出原始信号。

 

        然而，帐篷式滤波的效果并不顺滑，在采样点处会出现突然坡度变化，所以帐篷式滤波并不是完美重构滤波。为了得到完美重构效果，需要用到 低通滤波（low-pass filter），信号的频率组成部分是一个正弦波 ，sin(2πf)，其中f是频率。低通滤波会将所有高于滤波器所定义的某个频率的所有频率部分过滤掉。直观的，低通滤波消除了信号所有的尖锐特征，也就是模糊了信号。 理想的低通滤波是sinc滤波：

      

        在频域中理想的低通滤波是盒式滤波，当与信号相乘后，它会滤掉超过滤波宽带的所有频率。将盒式滤波从频域转换到空间域后就得到sinc函数，同时，乘法运算会转换为卷积。

 

        使用sinc滤波重建的信号的平滑效果很好，如图5.21所示。采样过程中信号引入了高频部分（突变），而低筒滤波的任务是消除这些成分。实际上，sinc滤波消除了所有频率高于采样率1/2的正弦波。如公式5.22所示，当采样率是1的时候（采样信号的最大频率要小于1/2），sinc函数是理想重构滤波。更一般地，假设采样率是fs，则相邻采样点之间的间隔是1/fs。这种情况下，理想的滤波是sinc（fs x），并且会消除所有高于fs/2的频率。当重采样信号的时候，这也很有用。但是 ，sinc的滤波宽度是无限的，并且在某些区域值是负的，所以在实际中很少使用。

 

图 5.21 利用sinc滤波重构原始信号。sinc滤波是理想的低通滤波。

 

        一方面盒式滤波和帐篷式滤波的质量不行，另一方面sinc滤波不适合实践，使用最为广泛的是介于这些之间的。滤波功能近似于sinc滤波，但是限制了它们能影响到的像素数量。最接近sinc滤波的滤波都有部分区域值是负值，对于应用，负值是不理想的或不能用于实践的。通常使用的是 无负波瓣的滤波（通常称为高斯滤波）。12.1节将会详细讲到。

 

        使用滤波后将会得到一个连续信号，但是在计算机图形学中并不能直接显示连续信号。因此需要使用重采样。

 

重采样（Resampling）

        重采样主要是放大或缩小采样信号。假设原始采样点的坐标都是整数（0、1、2，…），即样本之间具有单位间隔。进一步假设在重采样后，新的采样点的坐标之间的间隔是a。对于a > 1，缩小采样（降采样），对于a < 1，放大采样（升采样）。 

        放大倍数相较于更为简单，所以从放大开始讲起。假设如上一节所示那样重构了采样信号，由于限制信号已被完美重建且是连续的，因此需要做的就是以固定间隔对重构的采样信号进行重采样，这个过程如图5.22所示。

图 5.22 左图是采样信号和重构后的信号。右图是对重构后信号以两倍采样率重采样后的信号，放大了信号。

        然而，缩小信号这种方法就不行了。为了避免走样， 原始信号的频率对采样率来说太高了，取而代之的是，用sinc（x/a）滤波来创建一个连续信号，然后，重采样，如图5.23所示。换句话说，这里用sinc（x/a）作为滤波，低通滤波的宽度会增加，所以信号很多的高频部分都被消除了。如图所示，滤波的宽度（单个sinc的宽度）加倍，会将重采样率降到了原采样率的一半。如果将这和数字图像关联起来，这类似于首先进行模糊处理（除去高频部分），然后以低分辨率对图像进行重采样。

图 5.23 左图是采样信号和重构后的信号。右图采样间隔翻倍后滤波宽度也翻倍，这样就缩小了信号。

5.4.2 基于屏幕的反走样（Screen-based Antialiasing）

        如果采样或滤波做的不好，三角形边缘会出现明显的瑕疵，阴影边界，镜面高光和其他颜色快速变化的现象都可能导致这类问题。本节讨论算法针对这些情况有助于提高渲染质量。它们都是基于屏幕的，都是仅对管线输出的样本进行操作。没有最佳的反走样技术，每个技术都自己的优势：渲染质量，捕获外形细节的能力，内存成本，GPU需求和速度。

        在图5.14所示的黑色三角形示例中，一个问题是低采样率。在每个像素的网格单元的中心采样一个样本，判断一个单元是否被覆盖是看单元中心是否被三角形覆盖。通过对每个屏幕网格单元使用更多样本并且以某种方式混合它们，可以得到更好的颜色，如图5.24所示。

图 5.24 左图展示的是一个像素只进行一次采样，因为三角形并未覆盖住采样点，所以像素颜色是白色，尽管像素部分被红色三角形覆盖。右图是一个像素用了四次采样，并且有两个采样点被红色三角形覆盖，所以像素的最终颜色为粉红色。

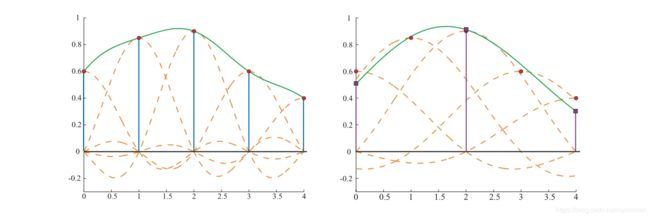
        基于屏幕的反走样方案的一般策略是对屏幕进行采样，然后对样本加权求和产生一像素颜色，P：

其中n表示一个像素被采样的次数。c(i,x,y)函数是采样颜色，Wi是权重（范围为[0,1]）。根据样本在序列中的位置（1,…,n）来获取样本的位置，函数还可以选择使用像素位置的整数部分（x，y）。换句话说，每个样本在屏幕网格上采样的位置都不同，并且对不同的像素选择采样不同的采样模式。在实时渲染中通常使用的是点采样。因此，c函数可以被视为两个函数。首先，f(i,n)检索采样点在屏幕上的浮点位置(xf , yf )，然后在屏幕上该位置进行采样，即检索该精准位置处的颜色值。其中另外一个变量是Wi，即每个样本的权重，这些权重加在一起等于1。在实时渲染系统中每个样本的Wi都是一样的，例如，Wi= 1/n。对于图像硬件的默认模式是，对像素中心的的一次采样，也就是反走样方程中最简单的例子。

        反走样算法中每个像素计算超过一个完整样本的算法称为超级采样（supersampling）算法，或者称为过采样算法（oversampling）。从概念上讲，全场景反走样（full-scene antialiasing，FSAA）也是超级采样反走样（supersampling antialiasing），以高分辨率渲染场景，然后以相邻的采样进行滤波来创建图像。例如，需要一个1280x1024的图像，如果离屏渲染出一个2560x2048的图像，然后对每2x2像素区域求平均，生成的图像就是所求的图像，每个像素采样4次，并使用了盒式滤波过滤，对应着图5.25中的2x2网格采样。这种方法的成本很高，因为所有的子样本都需要着色和填充，每个样本都有深度缓冲（z-buffer）。FSAA算法的主要优势是简单，此方法的其他低质量版本仅对屏幕一个轴以两倍采样率进行采样，因此称为1x2或2x1超级采样。通常为了简化，使用的是2的幂次方的分辨率和盒式滤波。NVIDIA的动态超级分辨率功能就是超级采样的一种更精细形式，场景用更高的分辨率进行渲染，使用13个样本高斯滤波来生成所需图像。

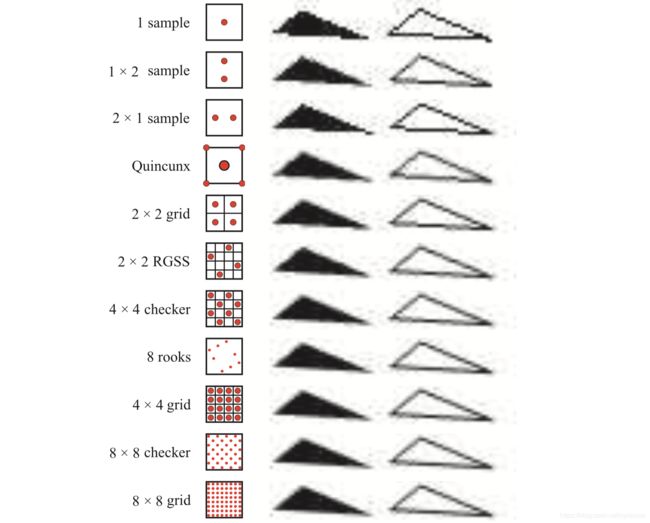
图 5.25 一些采样方法的对比。Quincunx共享了边角样本，并且中心样本的加权值占整个像素的一半。2x2的旋转网格（2x2 RGSS）比2x2正网格（2x2 grid）能捕获更多水平边缘上的灰度值。同样，8 rooks 模式要比4x4网格（4x4 grid）模式在这些线上能捕获更多灰度值，尽管使用的样本数要少。

        有一个和超级采样有关的采样方法是基于积累缓冲（accumulation buffer）的。此方法使用了和所需图像相同分辨率的一个缓冲区，代替了很大的离屏缓冲，但每个通道具有更多的颜色位。对场景进行2x2网格采样，需要生成4张图像，并根据需要视图在屏幕x和y轴方向上移动半个像素距离。生成的每个图像都是基于网格单元内的不同采样位置。额外花销就是不得不每帧多绘制几次场景，并把结果复制到实时渲染系统的算法中，这个成本也很贵。当需要高质量的效果的时候，这种方式很有用，因为每个像素可以使用的样本数和采样位置都是没有限制的。积累缓冲曾经由单独的硬件支持，如今OpenGL API可直接支持，但在3.0版本中已启用。在现代GPU中，积累缓冲概念可以在像素着色中实现，通过对输出缓冲使用一个更高精度的颜色格式。

        当物体边缘，镜面高光和其他尖锐阴影引起的颜色突变时，是需要进行一些额外的采样。使阴影变柔和，高光更平滑，通常可以避免走样。一些特定类型物体可以通过增加大小，例如电线，来确保它们在长度上每个位置至少覆盖一个像素。物体边缘的走样仍是采样的主要问题。可以根据分析，在渲染过程中检测到物体边缘则需考虑到走样问题，但着会比简单获取更多样本开销更大且更不稳定。然而，GPU功能，像保守光栅化（conservative rasterization）和光栅化顺序视图（rasterizer order views）为此打开了新的可能性。

        像超级采样和积累缓冲这类技术都是对着色和深度完全单独计算的，因为每个样本都会完整执行一次像素着色过程，所以成本相当高，整体上效率很低。

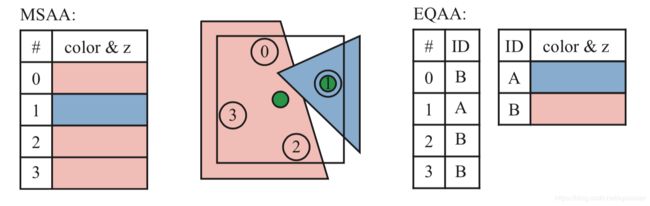
        多重采样反走样（multisampling antialiasing，MSAA）每个像素只执行一次像素着色过程，并且会在样本间共享该结果，从而降低了高计算成本。每个像素有四个采样位置，并且每个都有自己的颜色和深度值，但对每个片元的像素着色过程只评估一次。如果MSAA所有的采样位置都被片元覆盖，则对像素中心进行像素着色评估。相反，如果片元仅包含较少的采样位置，则计算像素着色的样本位置会移动到更好的位置。这样可以避免图像边缘采样的丢失。这个调整的位置称为重心采样（centroid sampling）或重心插值（centroid interpolation），并且是由GPU自动完成。如图5.26所示。

图 5.26 中间图展示的是一个像素被两个物体覆盖，其中红色物体覆盖了三个采样点，蓝色物体覆盖一个采样点，绿色圆点是像素着色的评估位置。因为红色物体覆盖的像素中心，所以像素中心是红色物体像素着色的评估位置，而蓝色物体的像素着色评估位置就是采样点位置。对MSAA来说，每个采样点都自己的颜色和深度值。右图展示的是EQAA的2f4x格式，四个采样点都有对应的ID，并由表格记录了每个ID值对应的颜色和深度值。

        多重采样反走样（MSAA）要比淡出的超级采样反走样（SSAA）机制快得多，因为每个片元只需要执行一次像素着色。它着重于已更高的速率对片元的像素采样，并共享其计算结果给最终着色颜色。它为进一步解耦采样和覆盖节省了很多的内存，反过来又是的反走样变得更快，涉及的内存越少渲染速度久越快。NVIDIA在2006年推出了覆盖采样反走样技术（coverage sampling antialiasing，CASAA），AMD随后推出了增强质量反走样技术（enhanced quality antialiasing，EQAA）。这些技术都是通过以较高的采样率且仅存储片元覆盖范围来工作的。例如，EQAA的2f4x模式存储的颜色值和深度值，在四个采样点间共享。这些颜色值和深度值并不存储在特定位置，而是存储在表格中，每个采样点只需要一个bit来指定和它所在位置存储相关的两个值。图5.26展示了覆盖的样本对每个片元最终像素颜色的贡献。如果存储的颜色数量超出了限制，则删掉存储的颜色并标记为未知。这些颜色对最终颜色没有贡献。对大多数场景，很少有像素同时被三个或更多不透明片元包含。但是，对一些最高质量的游戏，例如《Forza Horizon 2 went，极限竞速2:地平线》，采样了4倍MSAA，尽管EQAA具有很好的性能优势。

        一旦将所有几何都渲染进一个多重采样缓冲中，随后就需要进行解析操作。这会将所有采样颜色求平均值来决定像素的最终颜色，需要注意的是，当使用具有高动态范围颜色值的多重采样时，会有问题。这种情况下，为了避免瑕疵，通常需要在解析前进行色调映射（tone-map）。这可能很昂贵，但是可以使用简单近似色调映射的函数或其他方法。

        默认情况下，MSAA采样盒式滤波进行解析。2007年，ATI引入了自定义滤波反走样（custom filter antialiasing，CFAA），使用或窄或宽的帐篷式滤波，这些滤波会延伸到其他的像素单元中，这种模式已经被EQAA取代了。在现代GPU中，像素着色器或计算着色器都可访问MSAA样本，无论使用什么滤波进行重构，包括了从周围像素样本中取样。较宽的滤波会减少走样，尽管会丢失一些尖锐细节，Pettineo发现，使用滤波宽度为2个像素或3个像素的三次平滑步长（cubic smoothstep）或B样条（B-spline）滤波效果最好。但这会有性能成本，因为即使使用的是默认的盒式滤波解析对自定义着色都会花费很长时间，而一个更宽的滤波内核意味着增加更多的采样访问成本。

        NVIDIA的内置TXAA支持类似于使用比单个像素更宽的重构滤波，效果不错。TXAA和较新的MFAA（多帧反走样，multi-frame antialiasing）机制都使用了时间域反走样（temporal antialiasing，TAA）技术，可以使用前先帧的结果来改善图像。

        想象一下，通过生成一系列图像来“手动”执行采样，其中每个图像都是在像素内不同采样点位置进行渲染得到。这种偏移是通过在投影矩阵上附加一个微小平移来完成的。生成的图像越多，计算平均值的结果越好。这个使用了多偏移图像的概念被时间域反走样算法用到了，使用MSAA或其他方法生成一张图像，然后和先前的图像进行混合，通常用到2帧或4帧。较老的图像的权重较轻，因为这会导致帧闪烁，所以通常只对最近一帧和当前帧进行相等加权。由于每帧的样本位于不同的子像素位置，因此这些样本的加权总和要比单个帧具有更好的边缘覆盖率评估。如果使用最近两帧进行加权平均会得到更好的效果。每帧都不需要额外的采样，使得这种方法很吸引人。甚至可以使用时间域采样来生成一些低分辨率图像，然后这些图像会被放大到显示器分辨率。另外，光照算法或其他技术可以使用较少的样本，而是通过混合多帧来得到更好的结果。

        要想为静态场景提供反走样且步添加额外采样成本，使用时间域反走样的时候会有点问题。如果每帧的权重不一样，在静态场景中的物体可能会出现，而快速移动物体或快速移动摄像机可能会导致重影，这是因为上一帧对当前帧造成的影响。重影的一种解决方案是近对缓慢移动的物体进行反走样处理。另外一种重要方法是使用重投影（reproduction）来关联先前和当前帧的对象。在这些方案中，物体的移动向量存储在一个单独的“速度缓冲（velocity buffer）”中，这些向量用来关联先前和当前帧的，即从当前像素位置减去向量来找到上一帧物体表面的颜色像素。因为不需要额外的采样，所以时间域反走样也不需要多少额外的工作量，这种算法近几年引起了广泛的关注和采用。之所以会有关注，是因为延迟着色技术（deferred shading）和MSAA及其他多重采样技术不兼容。Wihlidal介绍了如何将EQAA，时间域反走样和各种滤波技术组合起来应用到checkerboard 采样模式中，提高质量的同时还降低了像素着色的调用次数。

采样模式（Sampling Patterns）

        有效的采样模式是反走样的一个关键因素。Naiman指出，人类在近水平和近垂直边缘上对走样最为敏感，倾斜度近45度的边缘是第二敏感。旋转网格超级采样（Rotated grid supersampling， RGSS）采样旋转正方形方式在像素内提供了更多的水平和垂直方向上的分辨率，如图5.25有展示这种模式。

        RGSS是一种拉丁超立方体（Latin hypercube）或N-rooks模式采样，将n个采样放在nxn网格中，每行和每列一个。在RGSS中，4个采样点分别位于4x4子像素网格的行列上。和常规2x2网格模式相比，这种模式特别适合捕获水平和垂直方向上的边缘。

        N-rooks模式是创建一个好采样模式的开始，但还不够。例如，所有的采样点都沿着子像素网格的对角线放置，所以几乎平行于这条对角线方向上的边缘的效果很差，如图5.27所示。为了更好的采样，要避免两个采样点彼此靠的太久，还希望采样点分布均匀在整个区域内。为了形成这种模式，分层采样技术（例如，拉丁超立方体采样，Latin hypercube sampling）和其他方法（例如，抖动（jittering），霍尔顿序列（Halton sequences），柏松圆盘（Poisson disk）等采样技术）相结合。

图 5.27 N-rooks采样。左图是一个标准N-rooks模式，但是它在捕获沿着对角线的三角形边缘的效果很差，因为随着三角形移动，这些采样点位置要么全部在三角形内部，要不全部在三角形外面。而右图的模式则更有效果。

        实际上，GPU制造商通常将这种采样模式硬连接到硬件中，以进行多重采样反走样，图5.28展示了实际中使用的一些MSAA模式。对时间域反走样，覆盖模式（coverage pattern）是编程人员想要的。因为采样点的位置可逐帧变化。

图 5.28 适用于AMD和NVIDIA图像加速的MSAA采样模式。绿色圆点是最终着色采样的位置，红色圆点是计算和保存采样点的位置。从左到右，依次是2x，4x，6x（AMD），和8x（NVIDIA）采样。

        虽然子网格模式可以很好地近似每个三角形如何覆盖网格单元，但是这并不理想，场景可以由任意物体组成，在屏幕上有可能会很小，这意味着没有任何采样率会完美捕捉到它们。如果这些微小物体或特征形成图安，以恒定间隔采样的话可能会导致莫尔条纹或其他干涉图案。网格模式在超级采样中特别容易出现走样。

        有一种解决方案是使用随机采样（stochastic sampling），如图5.28所示的模式。随机化会让瑕疵看起来像噪声，人类的视觉系统对此会更容易忘记。结构较少的模式虽有帮助，但是在像素之间重复时仍会有走样。所以有一种解决方案是对不同的像素使用不同的采样模式，或动态改变每个采样点的位置。在过去的几十年里，偶尔会有硬件支持交错采样，即一组像素中的每个像素具有不同的采样模式。例如，ATI的SMOOTHVISION允许每个像素最多16次采样，并且最多可以用16个用户定义的采样模式。

        一些其他的GPU支持算法也值得注意。有一种实时的反走样机制：NVIDIA的旧版Quincunx方法，会让一个采样点影响超过一个像素。“Quincunx”是指五个对象的排列，四个在一个正方形上，第五个在正方形中心。Quincunx 多重采样反走样方法就是使用的这种模式，让四个采样点分布在像素的四个角上，见图5.25，每个采样点的值会分配给四个相邻的像素。每个采样点的权重分配是：中心采样点的权重值是1/2，而四个角上的采样点的权重值都是1/8。正是这种分享机制，每8个采样点平均只需要2个像素，结果明显要优于行2 sample FSAA方法。该模式近似于帐篷式滤波，如上一节所说，要优于盒式滤波。

        如果一个像素一次采样，Quincunx采样模式也可以应用在时间域反走样上。每一帧和前一帧都会每个轴上有半个像素的偏移，偏移方向在帧之间交替。前一帧给当前帧提供像素四个角的采样，然后用双线性采样（bilinear interpolation）快速计算出对每个像素的贡献，最后和当前帧的结果取平均值。每个帧的权重值相等时，意味着在静态视图里没有闪烁，而在齐次移动物体上还有问题，但仍比每帧每个像素仅一次采样的效果好很多。

        如果在单帧中使用Quincunx模式，因为在像素边界共享采样点，所以像素边界采样成本很低，只有两次采样。RGSS模式更合适捕获近似水平和近似垂直方向上的灰度值。在移动设备图形上，最先使用的是FLIPQUAD模式，结合了这两个理想功能。它的优势是每个像素只有两次采样，并且质量类似于RGSS（成本是每个像素四次采样）。这个采样模式如图5.29所示。

图 5.29  左侧展示的是RGSS采样模式，成本是每个像素四次采样。通过将这些采样点位置移动到像素边缘，采样点就会被各像素边缘共享。但是，其他的每个像素必须具有一个反射采样模式，如右图所示。右图的模式被称为FLIPQUAD采样模式，成本是每个像素两次采样。

        和Quincunx一样，两次采样的FLIPQUAD模式也可以用在时间域反走样中。Drobot 解决了他在HRAA（hybrid reconstruction antialiasing）工作中的问题，他在探索两次采样中哪种模式最好，最后他发现FLIPQUAD是他探索的五种模式中最好的。checkerboard模式也同样适用于时间域反走样。EI Mansouri 讨论了用两个采样的MSAA来创建一个checkerboard渲染，以减少成本的同时解决走样问题。Jimene使用了SMAA时间域反走样技术，这个技术的反走样质量可以响应引擎负载而改变。Carpentier和Ishiyama通过旋转采样网格45度，在像素边缘进行采样，他们将这种时间域反走样机制和FXAA结合在一起，可以在高分辨率上高效渲染。

形态学方法

        走样通常是边缘引起的，例如几何形状边缘，尖锐的阴影或明亮高光形成的边缘。2009年Reshetov提出了一种算法，称为形态反走样（morphological antialiasing，MLAA）。“形态”意味着和物体的形状或结构有关。早在1983年，Bloomenthal就在这一领域做了早期工作。

        这种反走样是在后期处理中完成的，也就是，在完成渲染后，然后把渲染结果进行反走样处理。自2009年以来，以及开发出了各种各样的技术。那些依赖其他缓冲（深度缓冲、法线缓冲等）的算法，像SRAA（subpixel reconstruction antialiasing），可以提供更好的结果。分析方法，例如几何缓冲反走样（geometry buffer antialiasing，GBAA）和距离边缘反走样（distance-to-edge antialiasing，DEAA），让渲染器计算了三角形边缘的位置的附加信息，例如，边缘距离像素中心的距离是多少。

        大部分机制只需要颜色缓冲，意味着它们还需要改善阴影边界，高光或各种预先应用的后期处理技术。例如，定向局部反走样（directionally localized antialiasing，DLAA），近似垂直的边缘应水平模糊，同样，近似水平的边缘应该垂直模糊。

        边缘检测的更复杂形式是尝试去找到可能以任意角度包含边缘的像素，并确定它的覆盖。检查周边潜在的边缘，尽可能的重建出原始边缘所在位置。边缘对当前像素的贡献可以用来和相邻像素的颜色进行混合。如图5.30所示。

图 5.30 形态反走样（morphological antialiasing）。左图是走样图像。目的是确定边缘可能的方向。中间图展示了通过检测相邻像素来记录是边缘的可能性，给出了两种可能是边缘的示例。在右图，找到最佳猜测边缘，把相邻像素的颜色和当前像素的中心位置的颜色进行混合，混合比例和像素覆盖率成比例。对图中每个像素重复此过程。

        基于图像的算法有几种容易会人歧途。首先，如果两个对象之间的色差低于算法的阈值，可能会检测不到边缘。具有三个或更多不同表面重叠的像素很难检测。具有高对比度或高频元素的表面，像素之间颜色快速变化，会导致算法丢失边缘。特别的，将形态学反走样技术用在文本上，文本通常会有影响。物体的边角会是一个挑战。单个像素的改变可能会引起边缘重构发生较大变化，会在帧与帧之间有明显的瑕疵。解决此问题的方法有，使用MSAA覆盖蒙版（MSAA coverage masks）来改善边缘检测。

        形态学反走样方案只能使用被提供的信息。例如，一个物体的宽度要小于一个像素的宽度，例如电线或绳索，会在屏幕上没有覆盖住像素中心位置有空隙。这种情况下，采集更多样本会提高质量，仅仅依靠基于图像的反走样上不行的。另外，执行时间可以根据查看的内容而变化，例如，一片草地所需要的反走样时间是天空的三倍。

        综上所述，基于图像的反走样技术只需要少量的内存及处理成本，所以在很多应用程序中都有用到。最流行的两种算法是快速近似反走样（fast approximate antialiasing， FXAA）和子像素形态反走样（subpixe morphological antialiasingl，SMAA），部分原因是两者都提供了不同设备的可靠的免费的源代码。都有自己可用的各种设置，在速度和质量间进行权衡。每帧的成本通常在1-2毫秒的范围内，这是游戏愿意花费的时间。最后，两种算法都可以使用时间域反走样（TAA）。Jimenez提出了一种改进SMAA的实现，比FXAA更快，并给出了时间域实现方案。最后，推荐读者阅读Reshetov和Jimenez的形态技术及它们在电子游戏中的使用。

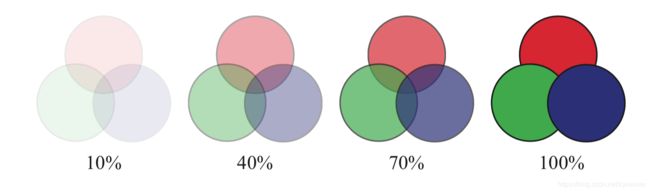
5.5 透明度，alpha值，合成（Transparency，Alpha，Compositing）

        有许多不同的方法可以使光线透过半透明物体。对于渲染算法，可以大致分为基于灯光效果和基于视图效果的。基于光的效果是指物体引起光衰减或转移从而照亮场景中其他的物体。基于视图的效果是指呈现半透明物体本身的效果。

        本节会讨论基于视图的半透明最简单形式，把半透明物体当作其后面物体颜色的衰减器。一种给人透明感的方法称为screen-door transparency。这个方法是用像素对齐的checkboard填充模式来渲染透明三角形，也就是说，其他像素也会被渲染，这样在半透明物体后的物体就部分可见。通常，屏幕上的像素距离足够近，以至于checkboard本身不可见。这个方法的缺点是在屏幕一块区域只能渲染一个半透明对象才让人信服。例如，如果在蓝色对象上绘制了半透明的红色对象和半透明的绿色对象，则三种颜色中，只会有两种可以显示在屏幕上。该技术的一个有点就是它的简单性，透明物体可以随时以任何顺序绘制，且不需要特别的硬件。

        由Enderton等人提出了随机透明度，利用subpixel screen-door 掩膜（masks）和随机采样相结合。一个理由是，通过噪声，利用随机点画模式来表示一个片元的alpha覆盖，如图5.31所示。每个像素需要大量的采样才能看起来结合合理，并且这对应着需要大量的内存。优势就是，不需要混合，并且已经考虑到了反走样，透明度和其他只显示部分像素的现象。

图 5.31 随机透明度。放大区域展示的是噪声的利用。

        大部分透明度算法会将透明物体的颜色和其后面物体的颜色进行混合，为此，alpha blending（alpha 混合）的感念被提出了。当一个物体被渲染在屏幕上时，每个像素都要使用到RGB颜色值和z缓冲区深度值，还有一个就是alpha值，它描述了一个物体片元对一个像素的不透明度和覆盖度。alpha值为1.0，则意味着物体上不透明的，并且像素的关注区域都被覆盖住了。等于0.0则意味着片元完全透明，像素完全没有覆盖到。

        alpha值可以视为不透明度或覆盖率，视情况而定。例如，肥皂泡的边缘会覆盖像素的四分之三，即0.75，几乎近似于透明，可以让十分之九的光线透过到达眼睛，所以它由十分之一是不透明的，即0.1。那么其alpha值为0.75x0.1 = 0.075。然而，如果我们利用了MSAA或类似的反走样算法，则采样点本身像需要考虑进覆盖率范围内。四分之三的采样点将收到肥皂泡的影响，然后在这些采样点中，我们将使用0.1不透明值作为alpha值。

5.5.1 混合顺序（Blending Order）

        为了使物体看起来半透明，需要把物体渲染在现有场景的最上层，并且它的alpha值得小于1.0。每一个被该物体覆盖到的像素，都会收到一个来自像素着色器的RGBA值，将这个片元的值和混合前的像素颜色使用over算子（over operator）进行混合，如下：

其Cs是透明物体的颜色（称为源），as是物体的alpha值，Cd是混合前的像素颜色（称为目标），C0则是最后混合后的最终颜色。实际上，如果RGBA是不透明的（as=1.0），则方程课简化为像素的颜色完全替换为物体的颜色。

例子：混合（Blending）。一个红色半透明物体渲染在一个蓝色背景上，物体的RGB为（0.9，0.2，0.1），背景的RGB为（0.1，0.1，0.9），物体的透明度为0.6。则混合后的颜色为：

最后颜色为（0.58，0.16，0.42）。

        over算子为渲染对象提供了半透明的外观。通过这种方式实现了透明，从某种意义上讲，只要透过它看到其后面的物体，就可以视为透明的。使用over因子来模拟真实世界中的薄纱织物效果，织物后面的对象在视图中被遮挡了一部分，因为织物的线上不透明的。实际中，宽松的织物的alpha覆盖率随着角度变化。这里的重点是alpha模拟了材质覆盖像素的程度。

        over算子在模拟其他的透明效果时效果不太令人信服，尤其是在透过有色玻璃或透过塑料观看时。在现实世界中，红色透明物体放置蓝色物体前面会让蓝色物体看起来较暗，因为反射的光线能透过红色物体的很少，如图5.32所示。当在混合时用over算子，结果是蓝色和红色叠加在一起。如果是两种颜色相乘，结果会好点。

图 5.32 一个红色的织物和一个红色塑料透明物体，具有不同的透明效果，注意，阴影也不同。

        在基本的混合阶段操作中，over通常是用于透明效果，另外一种有用的操作是additive混合（additive blending），将像素简单的求和。如下，

这种混合模式可很好的用于发光效果，例如闪电和火花，不让后面的像素衰减，而只会使它们变亮。但是这种模式并不适用于透明效果。对于具有好几层半透明的表面，例如烟雾或火，additive blending让其颜色更具有饱和。

        为了正确的绘制透明物体，需要在不透明物体之后绘制。首先，关闭混合，渲染所有的不透明物体，然后打开混合，再绘制透明物体。

        z-buffer的一个限制是，每个像素仅存储一个对象。如果在同一个像素上有好几个透明物体，仅依靠z-buffer是不能正确绘制出透明效果的。当在透明表面上绘制其他物体时，通常需要从后到前的顺序进行渲染，不这么做的话，会得到错误的效果。一种得到渲染顺序的方法是对存储每个物体的质心沿着视图方向的距离，并进行排序。这种粗略的排序效果不错，但是还有很多问题。首先，这个顺序只是一个近似值，可能有较远的物体出现在了较近的物体前面。物体不可能在任何角度的视图上解析成一个个网格，除非将每个网格分解成单独的碎片。如图5.33的左图所示。即使是单个具有凹面的网格，当在屏幕上出现重叠时，这时的排序是有问题的。

图 5.33 左图是仅利用了z-buffer的渲染透明物体示例，以任意顺序渲染网格会有严重错误。右图是利用了深度剥离（depth peeling ）技术可以得到正确效果，但成本会变多。

        尽管如此，但是由于它的简单性和快速，且不需要额外的内存或特殊GPU支持，这种粗略的排序还是经常被用到的。如果要实施，最好在执行透明度操作的时候关闭z深度替换功能。也就是说，z-buffer仍然测试正常，但是存在的曲面不会改变存储的z深度值，最接近的不透明表面的深度保持不变。用这种方式，所有的透明物体都会以某种形式出现，而不是在摄像机旋转时（没关闭深度替换功能的话，排序会出现变化）突然出现或消失。当然还有其他的技术可以帮助改善外观，例如，绘制每个透明网格两次，先渲染背面然后渲染正面。

        可以修改over算子方程，以从前到后混合得到相同的结果，这种混合模式称为under算子。

注意，under算子要求目标保持alpha值，而over算子是不需要的。换句话说，目标不是不透明的，所以需要具有alpha值。under公式和over公式很像，但是源和目标交换了。另外，计算alpha的公式和顺序无关，交换源alpha和目标alpha，结果是相同的。

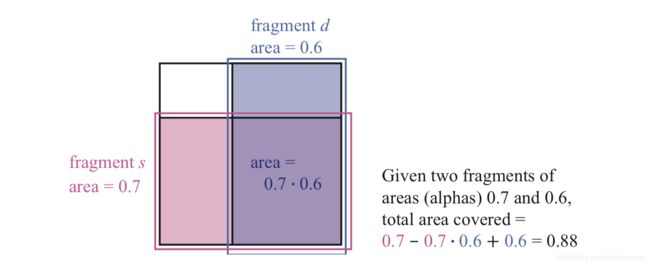
        alpha公式考虑的是片元的alpha覆盖度。Porter和Duff指出，由于不知道每个片元的覆盖区域的形状，假设每个片元覆盖另一片元是按其alpha比例来覆盖的。例如，如果as=0.7，那么像素被分成两部分，其中0.7被源片元覆盖，另外0.3没有。如图5.34所示。

图 5.34 一个像素和两个片元，s和d。将两个片元沿不同的轴对齐，两个片元对像素的覆盖率是各自独立的，两个片元都覆盖住的面积可以用公式求出。两个面积相加，然后减去重叠的面积。

5.5.2 顺序无关的透明度（Order-Independent Transparency ）

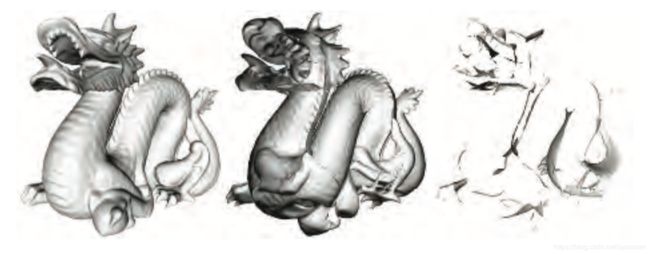
         under算子的方程将所有透明对象绘制到一个单独的颜色缓冲区，然后利用over算子将缓冲区的颜色混合到场景的不透明物体的视图上。另外一个利用under算子的是顺序无关的透明度（order-independent transparency，OIT）算法，深度剥离（depth peeling）。顺序无关意味着应用程序不需要进行排序。深度剥离后面的思想是利用两个z-buffers和多个passes。首先，渲染第一个pass，所有表面的深度值，包括透明表面，都存在了第一个z-buffer中。在第二个pass渲染所有的透明物体。如果一个物体的深度值和第一个z-buffer中的某值匹配上，我们就知道这是最近的透明物体的，把它的RGBA值存储到一个单独的颜色缓冲区中。然后剥离该层，如果保存的透明物体的深度值超过了第一个深度值，并且更靠近，那么这个深度值就是第二个靠近的透明物体。通过几个passes连续剥离和连续使用under算子添加透明层后，然后把透明图像混合到不透明的图像上，如图5.35。

图 5.35 每一个深度剥离的pass都会绘制一个透明层。左图展示的是第一个pass，这层是明显可以肉眼可见的。中间图是第二层，绘制的是第二靠近靠近透明表面，本例中是物体的背面，右图是第三层，是一组第三靠近透明物体的表面。最终结果如图14.33所示。

        已经发展出了好几种这种机制的变种。例如，Thibieroz给出了一种算法，优点是能够立马混合透明值，意味着不需要特殊的alpha通道。深度剥离有一个问题，多少个passes对应能捕获多少个透明层。一种硬件解决方案是提供一个像素绘制计数器，该计数器会显示在渲染过程中写入了多少个像素，当渲染一个pass时没有像素，则渲染完成。这时用under算子的优势就是，最重要的透明层，例如眼睛看到的第一层，会最早绘制。每个透明表面会增加当前像素的alpha值。如果alpha值接近1.0。混合会让当前像素变得几乎不透明，因此距离较远的物体的影响可以忽略不计。从前到后的剥离可以缩短，如果当渲染的像素数量低于某个值或达到了指定pass固定的次数。但这对从后到前的剥离行不通，因为通常最近的层时最后绘制，有可能会因提前终止而丢失。 深度剥离虽然有效，但是它时很慢的，每一层的剥离都是所有透明物体的单独的渲染pass。

        以合适的交互速率把透明物体混合在一起的问题不是缺少算法的问题，而是如何有效的将这些算法映射到GPU上的问题。1984年，Carpenter提出了A-buffer，另外一种形式的多重采样。在A-buffer中，每个渲染的三角形都会为其完全覆盖或部分覆盖的屏幕网格单元创建一个覆盖蒙版。每个像素都有一个列表来存储与其相关的片元。不透明的片元可以剔除它后面的片元，类似于z-buffer。所有的片元都是为了透明表面，一旦所有的列表都完成了，就可以通过遍历片元并解析每个样本来生成最终结果。

        在GPU上给每个像素一个片元列表的想法在DirectX11发布后成为了可能。DirectX11发布了很多新功能，包括无序访问视图（unordered access views）和原子操作（atomic operations）。通过访问覆盖蒙版并评估每个样本的像素着色，可以让MSAA反走样技术得以实现。

        A-buffer的优势是只有每个像素需要的片元需要分配，就像GPU上链表实现一样。在某种意义上，这样也是不利的，因为在一帧开始渲染之前不知道存储量。在场景中有头发，烟雾和其他潜在物体都会重叠在透明表面上，从而生成大量的片元。Andersson指出，对一个复杂的游戏场景，最多50个透明网格物体，例如树叶，或最多200个半透明粒子可以重叠。

        GPU通常有预先分配内存资源，例如缓冲区和数组，链表也不例外。用户需要决定多少内存是足够的，而内存不足会导致各种问题。Salvi和Vaidyanathan提出了一种方法解决这个问题，多层alpha混合（mult-layer alpha blending），利用了intel提供的GPU特征，像素同步（pixel synchronization），如图5.36所示。这种方法比原子操作开销更小，提供了可编程混合。这种方法重新定义了存储和混合，当内存不足时可以优雅的降低性能。DirectX 11.3引入了光栅化顺序视图（rasterizer order views），一种缓冲区，可以让任何支持这个功能的GPU都可以实现这种方法。移动设备有个类似的功能，称为瓦片局部存储（tile local storage），可以实现多层alpha混合。这种算法成本比较昂贵，会降低性能。

图 5.36 左上图是传统的从后到前的alpha混合，因为排序不对导致渲染错误。右上图使用了A-buffer，效果正确，是非互动结果。左下图使用的是多层alpha混合（mult-layer alpha blending）。右下图展示的是A-buffer和多层alpha混合的区别，为了可见乘以了4.

        这种方法是建立在Bavoil等人提出的k-buffer概念上，保存了前面几层可见层，并进行排序，而更深的层则进行了合并和丢弃。Maule等人使用了k-buffer并对较远的深层进行了加权平均。加权求和（weighted sum）和加权平均（weighted average）的透明技术和顺序无关，都是单pass，几乎在任何GPU上都可以运行。问题在于它们没有考虑物体的顺序，例如，利用alpha来表示覆盖率，红色纱巾在蓝色纱布围巾上显示出了紫罗兰的颜色，而不是一条红色围巾，上面透着一点蓝色。尽管对几乎不透明的物体的结果很差，这类算法对可视化很有用，对高度透明表面和粒子也效果很好。如图5.37所示。

图 5.37 随着不透明度的增加，物体的顺序变得越来越重要。

        加权求和透明的公式如下：

其中n表示的是透明表面的数量，ci和ai分别对应其透明值，cd是不透明部分的颜色。两部分相加就是每个像素最终的颜色。这个方法的问题有：总和饱和，即生成的颜色值要大于（1.0，1.0，1.0），并且背景颜色会取反，因为alpha的总和可能超过1.0。

        通常会选择加权平均，公式如下：

加权平均的一个限制是，对于相同的alpha，它会均匀混合所有颜色，不会考虑到顺序。McGuire 和Bavoil引入了加权混合的与顺序无关的透明算法（weighted blended order-independent transparency）。在他们的算法中，到表面的距离会影响权重，越靠近表面权重越大。而且，不是对alpha求平均，u的计算是，将项（1-ai）相乘在一起，然后1减去相乘的结果，这种算法会得出一组表面的真正的alpha平均值。这种算法会给出更令人信服的结果，如图5.38所示。

图 5.38 两个不同摄像机观察同一个引擎模型，都采样的是加权混合与顺序无关透明算法（weighted blended order-independent transparency）。按距离加权能够弄清哪些面更靠近观察者。

        一个缺点是，在较大的环境中，物体彼此靠的太近，按距离加权和加权平均的结果会没什么区别。另外，随着摄像机到透明物体的距离改变，深度权重虽然发生了变化，但是这种变化是渐进的。

5.5.3 预乘alpah和合成（Premultiplied Alphas and Compositing）

        over算子也可以用于混合图形或合成渲染对象，这个过程称为合成（Compositing）。每个像素中不仅存储了物体的RGB颜色值也存储了alpha值。由alpha通道形成的图像有时称为matte（影像形板），它显示了物体的轮廓形状。

        预乘alpha（premultiplied alpha）就是一种使用合成的RGBa数据的方式，RBG值在使用前先乘以了alpha值。这使得合成over算子方程更高效：

其中 是预乘源通道，替换了公式5.25中的。预乘alpha使得使用over算子和添加混合不需要改变混合状态，因为源颜色现在是在混合过程中添加。注意，预乘RGBa值中的RGB部分的值通常不大于alpha值，因为这样可创建一个特别明亮的半透明值。

        一个白色（1,1,1）三角形在边缘覆盖40%的像素，因为反走样，像素值会设置成灰色值0.4，则这个像素的颜色值存为（0.4,0.4,0.4）。如果存alpha值，则为0.4，是三角形覆盖的范围。RGBa值为（0.4,0.4,0.4,0.4），是一个预乘值。

5.6 显示器编码

        当我们计算光照、纹理或其他操作的时候，使用的值都假定为线性的。这意味着加法和乘法会按照预期工作， 然而，为了避免各种各样的视觉瑕疵，显示缓冲区和纹理中使用非线性编码也需要考虑到。例如，着色器输出颜色范围为[0,1]，然后将其提高1/2.2次幂，这就是伽马矫正（gamma correction）。对传入的纹理和颜色取反操作。在大多数情况下，你可以让GPU为你做这些事情。

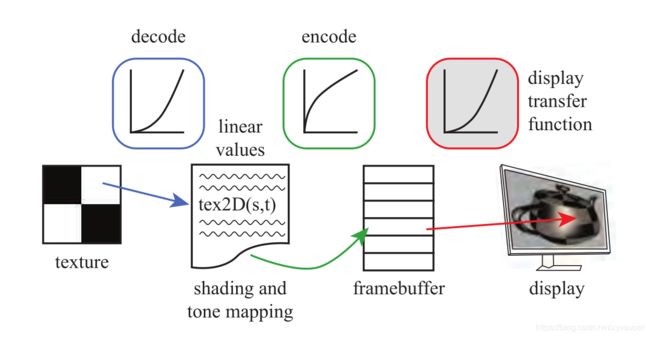
        当显示器对线性颜色值进行编码时，我们的目标是取消显示传递函数的影响，这样无论我们计算出什么值，都会发射出相应的辐射水平。例如，如果我们计算出的值是原来的两倍，我们想输出的亮度也是原来的两倍。为了保证这种关系，我们使用了显示传递函数的逆来抵消它的非线性影响。这种显示器响应曲线无效的过程又称为伽马矫正。当编码纹理值时，我们需要显示传递函数来生成一个线性值来给着色使用。图5.39展示了编码和解码在显示过程中的使用。

图5.39 左边是一个GPU shader访问一个PNG格式的颜色纹理，将其非线性编码值转换（蓝色）成线性值。经过着色和色调映射后，最终计算出的值被编码（绿色）并存储在帧缓冲中。这个值会和显示传递函数会决定发射出的辐射量（红色）。绿色功能和红色功能会相互抵消，这样发射出的辐射量就和线性计算出的值成比例关系。

        个人电脑屏幕的标准转换函数由一个叫sRGB的颜色空间规范来定义。当从纹理读取值时或颜色缓冲写入值时，大部分控制GPU的API可以设置成自动应用正确的sRGB转换。如6.2.2节讨论到的生成mipmap也会考虑到sRGB编码。首先转换成线性值，然后再进行插值，这样纹理间双线性插值也会正确工作。alpha混合中，需要将存储的值解码成线性值，然后混合新的值，最后再对新的结果进行编码。

        当值被写入到帧缓冲中，用于显示的时候，进行这个转换很重要的。如果在显示编码后进行后期处理（post-processing），这些效果会是在非线性值上进行计算，通常是不正确的效果，也会引起各种瑕疵。显示编码可以认为是一种压缩形式。考虑这个问题的一个好的方式是，用线性值来执行物理计算，并且无论何时我们想显示结果或访问可显示的图像（例如 颜色纹理），我们需要使用合适的编码或解码变换，将数据转换成显示编码形式或将数据由显示编码形式转换回来。

        如果你想手动应用sRGB，有标准转换方程或一些简化版本可以使用。实际中，显示器由若干位的颜色通道控制，例如，消费级别的显示器通常是8位，级别范围会是[0,255]。这里将显示编码的级别范围设为[0.0,1.0]，线性值得范围也是[0.0,1.0]。我们需要x是线性值，而存储在帧缓冲的y是非线性编码值。为了将线性值转换到sRBG非线性编码值，我们使用到了sRGB显示传递函数的逆：

其中，x表示的是线性RGB三个通道中的一个。这个方程会应用到每个通道，然后三个通道生成的值会组合一起来显示。手动使用这个方程需要注意，错误通常由使用编码颜色来代替它的线性值，还有对一个颜色进行了两次编码或解码。

        如果考虑到偏移量和缩放比例，这个函数可以简化为：

其中， γ = 2.2，希腊字母 γ就是伽马矫正这个名字的来源。

        静态或视频摄像机捕获的图像必须转换成线性值后才能用于计算。你在显示器或电视上看到的任何颜色都由显示编码RGB值，你可以通过屏幕截图或颜色选取获得这些值。这些值可以存储为PNG，JPEG，GIF等形式的文件，这些文件格式可以直接用于帧缓冲显示在屏幕上，无需转换。换句话说，你在屏幕上看到的都是显示编码数据。在着色计算中如果使用这些数据，必须将显示编码数据转换回线性值，可以用到sRGB转换：

其中，y表示一个规范化的显示通道值，例如存储在图像或帧缓冲中的值，范围在[0.0,1.0]。解码函数是之前用到sRGB公式的逆。解码函数和显示传递函数类似，因为存储在纹理中的值都是被编码过的。

        最简单的伽马显示传递函数是公式5.31的逆：

有时在移动设备或浏览器应用上会看到：

这是一种粗略的近似值，但是总比完全忽略的好。

        如果我们不关注伽马矫正，较低的线性值在屏幕上会显得很暗。一个相关错误是如果没有进行伽马矫正，有些颜色的色调会发生改变。我们说 γ = 2.2，我们希望从显示像素中发射出的辐射量和线性值成比例，需要对其进行计算，计算其的1/2.2次幂。线性值0.1对应0.351，0.2对应0.481，0.5对应了0.730。如果不进行编码，使用这些值的话，会引起发射出的辐射量比需要的少。注意，0.0和1.0并不会发生变化。

        忽略伽马矫正的另外一个问题是着色计算，对物理线性辐射值而言是正确的，但是对非线性值是不对的。如图5.40所示。

图5.40 两个重叠的聚光灯照亮了一个平面。作图中，在添加完光源（光照度分别为0.6和0.4）之后没有执行伽马矫正，加法是在非线性值上执行，引起了错误。注意，左边的亮度要比右边的亮度高很多，并且重叠部分的亮度不符合实际。右图，在添加完光源之后进行了伽马矫正，灯光本身亮度变得更亮了，重叠部分的亮度也变得合适了。

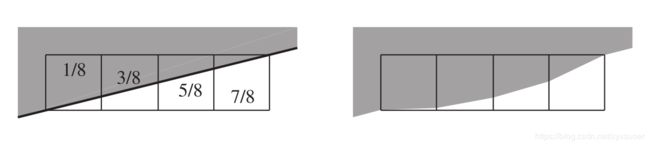
        忽略伽马矫正也会影响到对边缘进行反走的质量。例如，一个三角形边缘被四个屏幕网格单元覆盖（图5. 41），三角形的归一化亮度为1（白色），背景是0（黑色）。从左到右，网格覆盖了1/8,3/8,5/8和7/8。所以，如果我们使用合适滤波器，我们希望像素的归一化线性辐射度分别为0.125, 0.375, 0.625, 0.875。正确的做法是对线性值进行反走样，对四个结果值进行编码操作，如果这步没有做，那么像素的辐射度表现出来就会很暗，从右图就可以看到明显的边缘变形。这个叫做roping，因为边缘看起来像扭曲的绳索。图5.42就是这种效果。

图5.41 左图，在黑色（用灰色表示）背景上一个白色三角形的边缘覆盖了四个像素。如果没有进行伽马矫正，中间色调的变暗会引起边缘的感知的扭曲，如右图所示。

图5.42 左图，反走样的线是经过了伽马矫正的。中间图是经过了部分纠正的，而右边图是完全没有进行伽马矫正的。