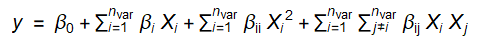RSM 学习笔记
*欢迎转载,请注明出处*
Note Author : yanbin chen
Email: [email protected]
Reference:
1.Advanced Signal integrity for High Speed Digital Design. Stephen H.HALL Howard L.Heck
2.JMP help.
The response surface modeling (RSM) technique provides a tool that gives us the ability to model the behavior of our signaling system as the circuit and interconnect characteristics vary.
RSM works by fitting a statistical model of the output response as a function of changes in the input variables.
The general form of the response surface model is
y is the system response. β is the model fit coefficients. x is the system input.
It is highly flexible, allowing to fit curved response surface by using higher-order combinations of input variables. In general ,second-order models are sufficient for high-speed signaling links.
§Step1 :get the system input and response matrix . Update it to 2nd-order matrix.
Input variable number is 5
The number of terms in the second-order model , k , is
1+2*5+5(5-1)/2=21
print (len(Doe_Var))
print (Doe_Var)
§Step2 :Norm the matrix.
Rather than use the raw data, regression tool usually fit the model to a transformed version of data.
2 kinds of normalization.
A: normalization. B: Round normalization.
Column1: original matrix X [constant x1 x2 x3 … x1x1 x1x2 x1x3 … xnxn]
Cloumn2 : mat_N_X[:,1:]=2*(mat_X[:,1:]-mat_X[:,1:].mean(0))/(np.ptp(mat_X[:,1:],axis=0)) # Normalized X
Cloumn3 : mat_N_X[:,1:]=np.around(2*(mat_X[:,1:]-mat_X[:,1:].mean(0))/(np.ptp(mat_X[:,1:],axis=0))) # Round Normalized X
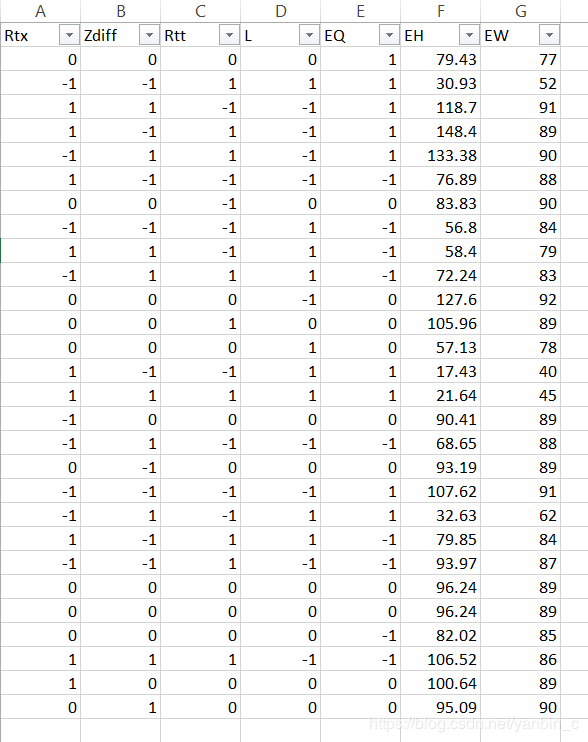
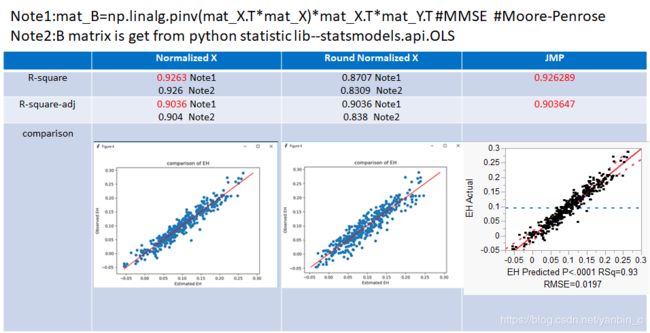
§Step3 :Regression analysis.
MMSE click another article..
https://blog.csdn.net/yanbin_c/article/details/84504273
Conclusion : The result shows normalized x is better than Round Normalized X in regression.
Why?Because our DOE table is not orthogonal array.
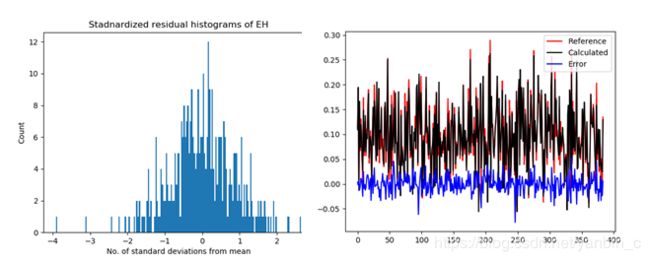
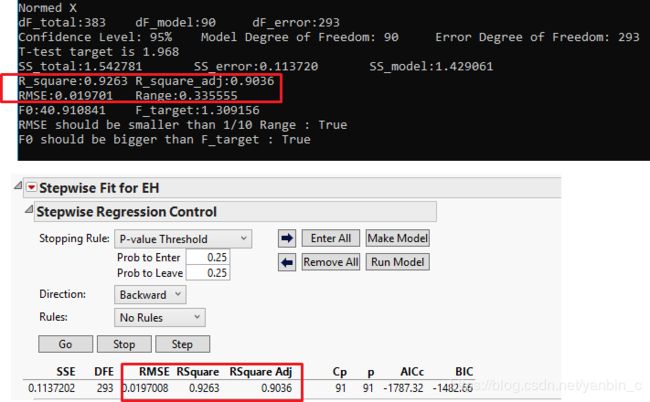
§Step4 :Measures of Fit.
Advanced signal integrity for High speed digital design -Section 14.4 page (615-618 )
Residuals vector / standard residual/R-square/R-square_adj/RMSE
§Step5 :Significant test. / Stepwise regression.
Model significance : the F-Test
![]()
Parameter significance : Individual t-Tests
the result fit well.
one key point. Expand JMP polynomial expressions in Mathematica