MySQL - 剖析MySQL索引底层数据结构

Pre

什么是索引？

通俗的说就是为了提高效率专门设计的一种 排好序的数据结构。

怎么理解呢？

举个例子哈

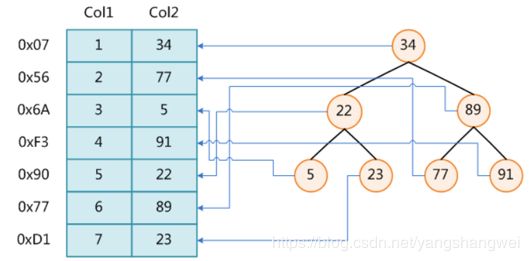
如上数据 ，假设有个SQL

select *  from t where  col2 = 22 ;

如果没有索引的话，是不是得逐行进行全表扫描，走磁盘IO…

如果加上一个合适的索引呢？

比如用一个二叉树

二叉树我们知道，右边的比左边大

那执行刚才的SQL的话，第一条记录是34 ，那我们查找的是22， 是不是就只要到它的左边查找即可，因为右边的数据都比34大，肯定没有22 ，找到22 以后, 搞定 ,I/O次数是不是比刚才的全表扫描的次数少很多，那效率自然就高了。

---

索引的数据结构选型

二叉树 ？

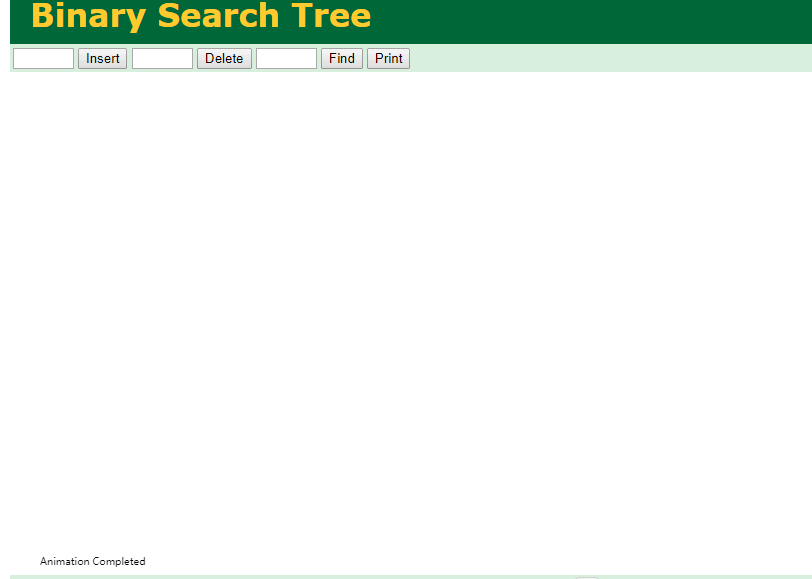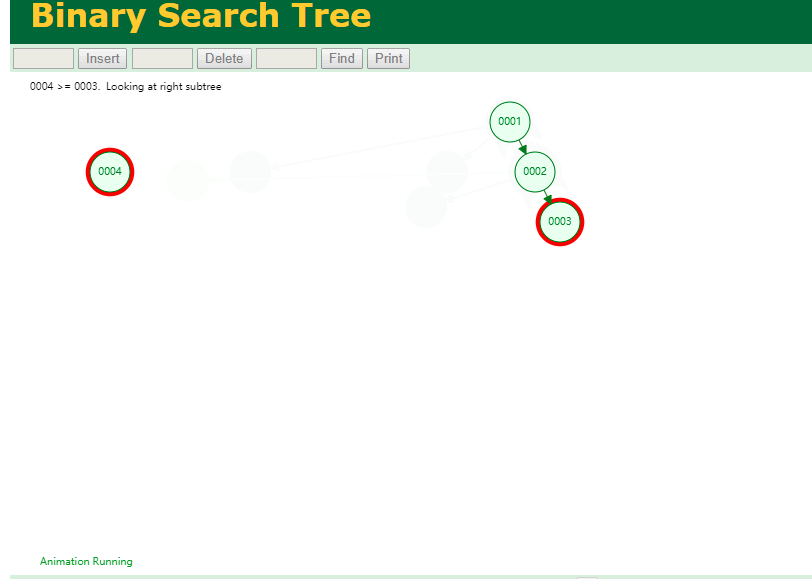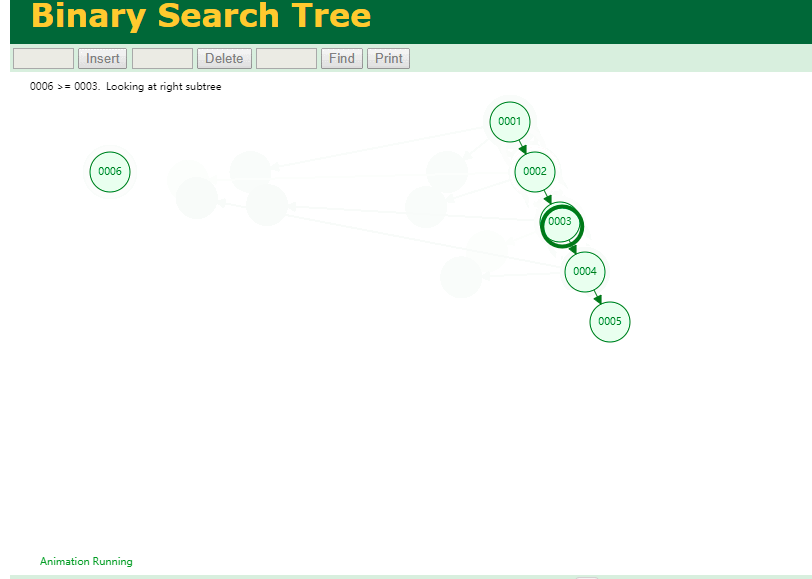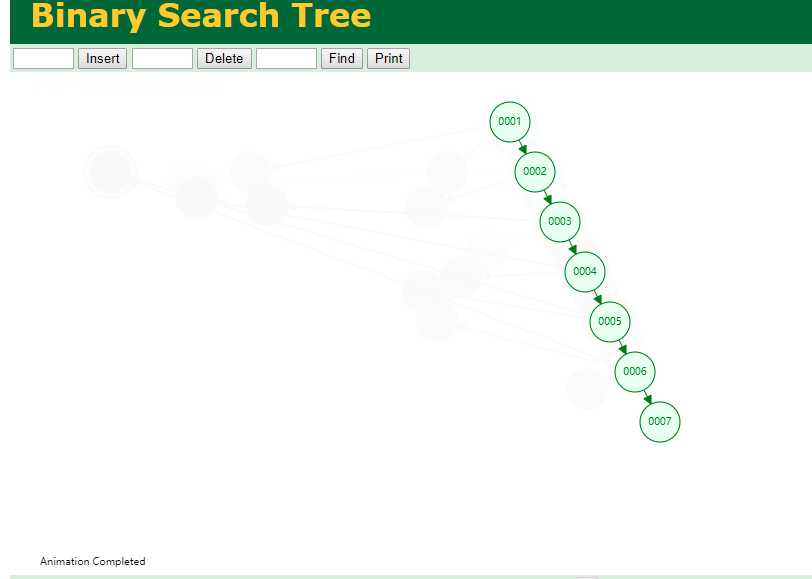
可以用二叉树吗？ 我们知道MySQL一般都有自增主键 ，id之类的字段

我们来演示下使用二叉树来存储这种自增的数据的话，会怎样？

https://www.cs.usfca.edu/~galles/visualization/BST.html

那查询

select * from t where id = 7

自增主键的时候 这个二叉树已经退化成链表了。。。。。

想想，一个几百万数据量的表 ，查找某个大一点的id , 逐个查找比对 （这些数据也是存储在磁盘上的，还得从磁盘上捞啊） 这I/O 这效率可想而知吧…

二叉树 pass ，不考虑了

既然退化成链表了，那试试带有平衡功能的树 二叉平衡树 （红黑树）？

自增主键， 退化为为链表

---

红黑树 ？

二叉树既然在某些情况下会退化成链表， 那如果这棵树能自动平衡呢？

这样子是不可能变成链表了，

同样 查询

select * from t where id = 7

三次磁盘I/O即可找到， 比刚才二叉树的七次是少了些哈 ，自然查找效率也比二叉树高了

可如果数据量几百万 上千万呢？

这棵树 得多高哇。。。

数据量大， 树高问题

那既然树高不好， 是不是如果可以控制树的高度（比如 3 到4层的高度，这样查询起来还能接受），让每一层能存储更多的数据，然后再分裂，这样的话数据量相乘起来，也是不少了对吧，这样就能存储更多的数据，这样会不会好一点？ ----> B-Tree

---

B-Tree ？

• 叶节点具有相同的深度， 叶节点之间指针为空
• 所有索引元素不重复
• 节点中的数据索引从左到右递增排列

叶子节点之间的没有指针，区别于B+树。

data存储的是数据对应的磁盘地址， k-v结构。

我们来看下B-Tree的插入 （Max.Degree 设置为3 即 元素到了3个就分裂 ）

查找一下

3次

MySQL也没有使用B-Tree , 因为

除了存储索引以外，还存储了data(数据对应的磁盘地址) ， 为了更多的存储数据，MySQL对B-Tree进行了很多改造

由此演进出了 B+Tree ，将data部分仅保留在叶子节点上，这样的话同等的页可以存储更多而索引数据。

---

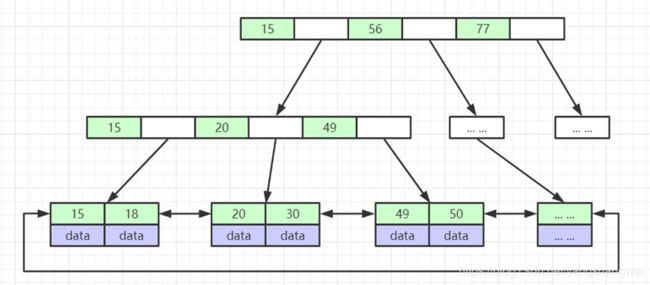
B+Tree

• 非叶子节点不存储data，只存储索引(冗余)，可以放更多的索引
• 叶子节点包含所有索引字段
• 叶子节点用指针连接，提高区间访问的性能

数据仅存储在叶子节点， data可能是磁盘地址也可能是其他的列数据，这个和存储引擎有关系。

叶子节点之间有指针相连。

我们来算下 3层高的B+Tree能存储多少数据结构

假设是BigInt类型的数据

BigInt 占 8个字节 ，同时还是用6个字节存储了它指向的数据的物理地址

MySQL在使用innodb引擎的时候页大小默认是16K ,查询如下

mysql> SHOW GLOBAL STATUS like 'Innodb_page_size';
+------------------+-------+
| Variable_name    | Value |
+------------------+-------+
| Innodb_page_size | 16384 |
+------------------+-------+
1 row in set (0.00 sec)

mysql>

假设 树高为3 ， 这样的话，第一层即可以存储 16KB * 1024 / (8B + 6B) = 1170

同样的第二层也是1170 （第二层不是叶子结点，不存储数据）

第三层，存储数据，一般情况下一行数据的大小肯定不会超过1KB，那我们就按照1KB算吧

3层高的B+Tree , 存储BitInt可以存储 1170 * 1170 * 16 = 2千1 百万。。。。这效率还是可以的哈

想一想 如果是4层高的数 1170 * 1170 * 1170 * 16 = 250多亿数据。.。。。

当然了 都是估算， 如果换成其他类型的数据，每个表的行数据的大小都是相关的，这也就是我们通常说的 MySQL的表到千万级别就要分库分表的理论依据了。

我们看下B+Tree的插入和查找

---

Hash表

• 对索引的key进行一次hash计算就可以定位出数据存储的位置
• 很多时候Hash索引要比B+ 树索引更高效
• 仅能满足 “=”，“IN”，不支持范围查询
• hash冲突问题

对索引字段进行hash以后， 还存储了数据对引得磁盘地址。

一般请款下，hash 比 b+tree的效率要高 ，但工作中绝大部分还是使用的B+Tree , 因为hash对范围查找不是很友好，还要全表扫描。

为啥B+Tree 支持范围查找？

我们知道B+Tree的叶子节点 有指针相连，从根节点找到对应的叶子节点后， 加上节点本身就是排好序的，所以范围查找就恨轻松了。

B-Tree 没有指针相连，所以要想范围查找，还得从根节点重新找，效率肯定比B+树低 。