聊聊KMP算法

KMP算法

前言

本文转载，觉得写得实在太通熟易懂了，因此收藏于博客中
原文：https://www.zhihu.com/question/21923021

背景

这几天自学了KMP算法，也在网上看了很多相关的博文，然而他们对next数组的求解方法的解释都比较模糊，难于让读者理解，故参考几位前辈的博文，加以优化，撰此博文，分享一下自己的理解。

简述BF算法

讲述KMP算法的原理之前，BF算法是绕不开的话题，也只有了解了BF算法，才能知道KMP算法的优势。
先来看一个例子：给出两个字符串A和B，求解A中是否包含B？如果包含，包含了几个？

BF算法的原理是一位一位地比较，比较到失配位的时候，将B串的向后移动一个单位，再从头一位一位地进行匹配。

如下图：

在比较到第6个字符时（字符索引：5），不匹配了，此时就要将B串后移一个单位，从头开始匹配（将原本指向A串第六个字符的指针i指向第二个字符，指向B串第六个字符的指针j重新指向B串开头）：

然而此时我们一眼可以看出第二次匹配也是必然失败的，但计算机并不知道，它只会按照BF算法一位一位的比较下去（在很多情况下要比较很多位才能发现不匹配），这种暴力求解的算法效率是极低的，所以我们有没有办法让计算机根据已经匹配过的部分知道自己从头匹配的时候应该忽略哪些部分，省去不必要的匹配？（在此例中即为从头跳过第二位的b从第三位开始新的匹配，例子不够极端，可能并不是很好理解跳过的必要性，请耐心看后续讲解）为了解决这个问题，KMP算法便诞生了。

KMP算法

前缀与后缀

首先我们要了解几个概念：前缀、后缀、相同前缀后缀的最大长度（为表述方便，下文均用公共最大长指代），为了直观一点，我们直接举例：

• abcdef的前缀：a、ab、abc、abcd、abcde（注意：abcdef不是前缀）
• abcdef的后缀：f、ef、def、cdef、bcdef（注意：abcdef不是后缀）
• abcdef的公共最大长：0（因为其前缀与后缀没有相同的）
• ababa的前缀：a、ab、aba、abab
• ababa的后缀：a、ba、aba、baba
• ababa的公共最大长：3（因为他们的公共前缀后缀中最长的为aba，长度3）

利用最大公共长度优化

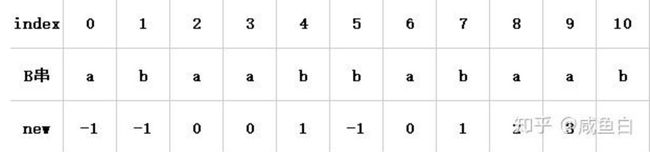
利用相同前缀后缀的最大长度（公共最大长）对匹配过程进行优化，如图：

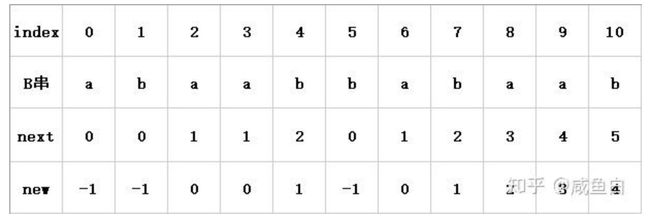
• index行是字符在B串中的位置索引值。
• B串行则记录了所有字符。
• next行则记录了当前从B串头部到当前位置的这一子串的公共最大长。（我们先不用管这些公共最大长是如何得到的，暂且假设是上帝告诉了我们）
• new行记录的值则是相应的公共最大长减去1。

好的，我们现在可以再次进行匹配了，还是开头的例子，B串在第6个字符处（索引5）失配，此时我们可以确认的是B串的前五个字符已经匹配成功了，让我们根据上面那个表格查找一下已经匹配成功的子串的公共最大长吧**（请注意是已经匹配成功的，我们在第6个字符处失配，所以应当去查找第五个字符或者说索引4的位置记录的公共最大长）**。

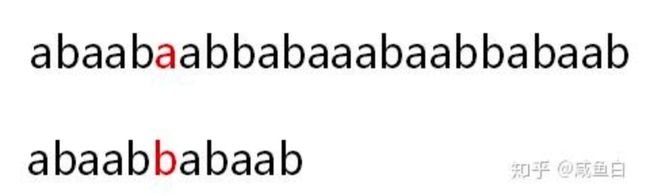
很明显，已匹配成功的子串（我们称之为C串吧）的公共最大长为2，这说明了什么？想一想，B串匹配成功的部分和A串失配处之前的一小部分子串都是C串，C串的公共最大长为2，C串最前面的两个字符（也就是B串的开头两个字符）和C串最后面的两个字符（也就是A串失配位前面两个字符）是相同的，这就意味着我们重新进行匹配的时候可以直接将B串的头部2个字符和A串匹配成功的部分的最后两个字符对齐。然后开始对比B串的第三个字符与A串的失配字符，进行新一轮的匹配。

关于对齐，计算机运行时是怎么做的？我们在匹配时分别用指针i和j指向字符串当前匹配的位置，失配之后指针i不变，继续指向A串的失配处，指针j则指向B串第三个位置（公共最大长的后面一位，索引为公共最大长）。

如下图：

蓝色的部分即是通过公共最大长直接匹配的位置，红色部分是重新开始匹配的位置（两个指针直接指向的位置），相较于BF算法，我们在这一步跳过了A串的第二个字符“b”，第三个字符“a”，直接将B串头部对齐了第四个字符，并从B串的第三个字符开始重新与此前失配的字符进行新一轮的匹配。实现就是如此简单，重新匹配的过程省去了一大堆不必要的匹配，为我们节省了很多时间。

也许有人会疑问，凭什么就应该跳过A串的第三个字符“a”去直接和第四个字符“a”进行匹配呢？难道从第三个开始匹配就不能成功吗？请回忆一下什么是公共最大长吧？是相同前缀后缀的最大长度。请对照着图6看完我下面的解释：我在前面有加粗这么一句话“B串的这部分子串和A串失配处之前的一小部分是相同的”，现在我们假设是从第三个字符“a”开始重新匹配的，如果要与B一直匹配成功到第五个字符“b”，也就是匹配成功了三个字符，这意味着什么？意味着第五个字符位对应的公共最大长应该是3，这显然是和事实的公共最大长为2是不符合的，以此类推，重新开始匹配时参考公共最大长是合理的最优解。再梳理一下其中的逻辑，现在你应该能理解公共最大长度的意义了。

等一等，我们好像忘了什么？原理懂是懂了，可上帝在哪？我们之前假设上帝告诉了我们next行（next数组中记录的值），可事实上上帝并不存在，还是得靠我们自己求值鸭！所以，怎么求next数组呢？

NEXT（NEW）数组的求解

在此我要先解释一下new数组中值的意义，正如表示公共最大长的next的数组的值同时表示了对应的最大前缀（为方便表示，我们将最大相同前缀后缀中的前缀称为最大前缀，最大相同前缀后缀中的后缀称为最大后缀）的后面一位的索引，new数组中的值等于next数组中的值减去1，我们同时用其表示了对应的最大前缀的最后一位的索引，这是为了后续的程序表达的便利，所以我们此处讲解对new数组的求解，因为求出了new数组等于求出来next数组。

先把求解new数组的类c伪代码贴在这里(B即为B字符串，new即为new数组，不要急于看懂代码，先看明白我的解释,代码看不懂也不碍事，反正是伪代码):

new[0] = -1
for (int i=1;i<n;i++) /* n为B串长度 */
{
    int j=new[i-1];   /* j为待计算位置前一位对应的new值，也就是最大前缀最后一位对应的索引 */
    while ((B[j+1]!=B[i])&&(j>=0))   /* 任何一个最大前缀后一位与当前求值字符相同时或者向前继续寻找的索引为-1时停止循环 */
        j=new[j];
    if (B[j+1]==B[i])  /* 字符相同，公共最大长+1，new值+1 */
        new[i]=j+1;
    else               /* 最终寻找到的索引为-1，公共最大长归零 */
        new[i]=-1;
}

首先，我们可以知道B串的第一个字符对应的公共最大长一定是0，在new数组中则为-1，所以new[0] = -1。接下来，我们不从第二个字符开始类推，而是选取一个位置靠后的具有普适性的例子以便更好的理解推导过程。

如下图：

假设我们已经一步步推导得出了前面0-9索引对应的new值，现在要求解索引10对应new值（再次提醒：这个值是公共最大长-1）。

我们首先需要考虑添加了字符b之后的公共最大长是否会增加1，该如何判断呢？

将索引10对应的字符和**前面已经求得解的最长字符串“abaabbabaa”**的最大前缀后面一位字符比较，如果二者相同，说明了最大前缀添加一位后产生的字符串和最大后缀添加了字符’b’产生的字符串相同，此时索引10位置对应的公共最大长应该在前面一位的基础上加1。

那么这个字符串**“abaabbabaa”**的最大前缀的后一位的索引值该如何找到？

这个值是已经求得解的最长字符串的公共最大长的值，即为next[9],或者说是new[9]+1。（next[9]对应了公共最大长的值，也表示着最大前缀后一位的索引）。

这个值具体是什么？

是new[9]+1 = 3+1 = 4。我们继续寻找索引4对应的字符，是’b’，和索引10对应的字符相同，所以索引10对应的公共最大长较之前一位加1，new值加1，所以new[10] = new[9]+1 = 3+1 = 4。

可是，如果B[10]不是’b’呢，如果B[10]=’a’呢？怎么办？

如下图：

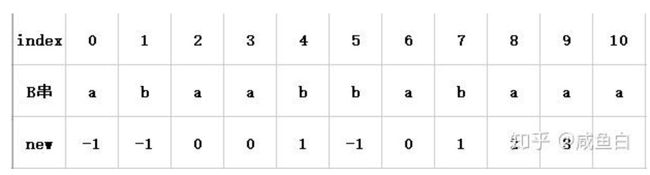
很明显，按之前的推理，在当前情况下，B[10]=’a’和B[4]=’b’是不等的，所以公共最大长不可能增加了，我们只能考虑其与前一位相等甚至减少的情况了，此时该怎么求呢？

我们现在要找的是最大前缀的前缀，与“最大后缀加‘a’字符”这一组合的后缀的公共最大长了，我们暂且将索引10前一位对应的子串的最大前缀与最大后缀称为C串吧（因为二者是相同的字符串），此时我们要求解的问题其实转化为了C串后面添加一个字符’a’对应的公共最大长，于是我们先利用索引10前面一位索引9对应的new值找到C串（从头数起）的最后一位，并重复上面的过程来推测此时公共最大长应该朝什么方向变化（这就是代码中循环的意义），如果向前找到的最后一位的索引是-1，即公共最大长已经减到0的时候，循环终止。现在回头再看看代码和注释，就应当能够理解了。（也就是说，如果当前最大公共前缀的往后一个字符不等于 新增的字符，则继续往前找前缀的前缀，看后面一个字符是否相等，如果找到是-1了，证明找完也没有相等的，那么新增字符就没有匹配的，那么最大公共长度就是0了，放到next数组中也就是-1）。

复杂度分析

KMP 算法的原理和实现我们就讲完了，我们现在来分析一下 KMP 算法的时间、空间复杂度是多少？

空间复杂度很容易分析，KMP 算法只需要一个额外的 next 数组，数组的大小跟模式串相同。所以空间复杂度是 O(m)，m 表示模式串的长度。

KMP 算法包含两部分，第一部分是构建 next 数组，第二部分才是借助 next 数组匹配。所以，关于时间复杂度，我们要分别从这两部分来分析。

我们先来分析第一部分的时间复杂度。

计算 next 数组的代码中，如果最大公共前缀的后一位和当前位的字符相等，则最大长度+1，否则往前找最大公共前缀，这个找的过程之前从之前next数组取，取的时间复杂度是O(1)，所以时间复杂度就是取的次数，即O(m)，m是模式串的长度。

我们再来分析第二部分的时间复杂度。分析的方法是类似的。

第二部分是匹配的过程，如果不匹配，就从next数组找出下一次进行匹配位置，那么这个取的时间复杂度是O(1)，所以匹配过程的时间复杂度取决于取的次数，最多为n次，因此这部分的时间复杂度为O(n)，n是主串的长度。

所以，综合两部分的时间复杂度，KMP 算法的时间复杂度就是 O(m+n)。

参考

KMP算法-知乎 参考“咸鱼白”这个人的回答

KMP算法解析—王争