基于R语言的Kaggle案例分析学习笔记(九)
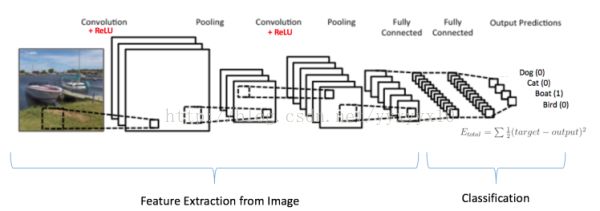
1、卷积神经网络的介绍
针对黑白图片:
1)局部链接
如上图所示,图片是由像素组成,而像素又是由很多数字组成,最左边的方框是4*4的像素图片,展开成那条橙黄色的长度的为16的向量,以4个像素为一个单位,映射到隐藏层的一个神经元,每个像素映射都有权重,每个被 映射的神经元都有一个常数b0。以input层的1、2、4、5像素为例,这4个像素映射到隐藏层的0号神经元,权重分别是w1、w2、w3、w4,常数为b0,相应的映射函数为:Y0=x0*w1+x2*w2+x4*w3+x5*w4+b0。
2)空间共享性
空间共享性是指任何像素组映射到卷积层的权重及常数项都是相等,例如现在红色方框框的是0、1、4、5这几个像素,下一步方框向右移动一步,框住1、2、5、6这几个元素,这几个元素对应橙黄色16个元素的向量分别也是1、2、5、6元素,这1、2、5、6元素映射到卷积层的1号神经元,有4个权重分别是w5、w6、w7、w8,这几个权重与w1、w2、w3、w4相同,常数项b0也相同。
3)输出表达
卷积层可以是向量也可以是一个矩阵,输出可以是向量的形式,也可以输出成一个矩阵,这样就形成了一张图片。
关于彩色图片的简单介绍:
原理与黑白图片类似,不同的是多了一个维度,黑白图片只有长宽两个维度,彩色图片还有深度这个维度。
如上图所示,彩色图片是三维的,由红绿蓝三个图层组成,每个图层的作用原理与黑白图片类似,单个图层的各个像素单元权重是共享的,但是不同图层的权重是独立的。
关于zero padding:
从以上关于黑白照片的详细介绍中可知,卷积层的神经元个数是小于输入的图片像素的,不断卷积,卷积层就不断减小,这样就会损坏图片像素,所以需要在卷积层外加多一层zero padding。如下图所示外围的小圆圈就是zero padding。
padding的大小可以根据以下的公式计算:Feature Map=(input_size+2*padding_size-filter_size)/stride+1
其中Feature Map的大小等于input_size。以上面图片为例,设padding_size为x,Feature Map=input_size=4,filter_size=3,stride=1,stide是步长,带入计算公式:
4=(4+2*x-3)/1+1,则可求出x=1.
3、R语言代码实现
这里主要使用亚马逊开发的用于深度学习的R语言包:mxnet包,数据下载地址:链接:http://pan.baidu.com/s/1nv5NMhb 密码:za7u
#下载安装
cran <- getOption("repos")
cran["dmlc"] <- "https://s3-us-west-2.amazonaws.com/apache-mxnet/R/CRAN/"
options(repos = cran)
install.packages("mxnet")
library(mxnet)
#加载数据
train <- read.csv("train.csv")
test <- read.csv("test.csv")
# Set up train and test datasets
train <- data.matrix(train)#变成矩阵
train_x <- t(train[, -1])#除第一列以外都作为输入值
train_y <- train[, 1]#目标列
train_array <- train_x
dim(train_array) <- c(28, 28, 1, ncol(train_x))#创建三维数组,因为手写图片是黑白图片,且大小为28*28的矩阵,一列代表一个数字,一共有ncol(train_x)数字
test_x <- t(test)
test_array <- test_x
dim(test_array) <- c(28, 28, 1, ncol(test_x))
#画个图
plot.digit<-function(x){
train.plot<-t(train[x,-1])#x代表画第几个图片
train.plot2<-matrix((train.plot),ncol=28)变成矩阵形式
image(train.plot2,col=grey.colors(225),axes=F)
}
data <- mx.symbol.Variable('data')#把数据变成mx规定的格式
# 第一层卷积层
conv_1 <- mx.symbol.Convolution(data = data, kernel = c(5, 5), num_filter = 20)#kernael就是filter,num_filter表示filter个数
tanh_1 <- mx.symbol.Activation(data = conv_1, act_type = "tanh")
#数据来自于卷积层,act_type激活函数为非线性函数即双曲正切函数
pool_1 <- mx.symbol.Pooling(data = tanh_1, pool_type = "max", kernel = c(2, 2), stride = c(2, 2))
#池化层,数据来自非线性激活函数,pool_type="max"最大池化法,stride表示移动步长
# 第二层卷积
conv_2 <- mx.symbol.Convolution(data = pool_1, kernel = c(5, 5), num_filter = 50)#护具来自第一层的池化层
tanh_2 <- mx.symbol.Activation(data = conv_2, act_type = "tanh")
pool_2 <- mx.symbol.Pooling(data=tanh_2, pool_type = "max", kernel = c(2, 2), stride = c(2, 2))
# 第一层全连接
flatten <- mx.symbol.Flatten(data = pool_2)#Flatten将矩阵变成一个向量,数据来自于第二层池化层
fc_1 <- mx.symbol.FullyConnected(data = flatten, num_hidden = 500)#全连接,全连接的数据来自上一层的flatten
tanh_3 <- mx.symbol.Activation(data = fc_1, act_type = "tanh")#加一层非线性激活函数,数据来自上一层的全连接
# 第二层全连接
fc_2 <- mx.symbol.FullyConnected(data = tanh_3, num_hidden = 40)#来自上层非线性的结果
#输出,因为这是多分类问题,所以用softmax函数
NN_model <- mx.symbol.SoftmaxOutput(data = fc_2)
# 设置种子,使结果具备可重复性
mx.set.seed(100)
# 使用cpu设备
devices <- mx.cpu()
# 训练
model <- mx.model.FeedForward.create(NN_model,
X = train_array,
y = train_y,
ctx = devices,#设备
num.round = 25,#迭代次数
array.batch.size = 40,#批处理规模
learning.rate = 0.01,#学习率
momentum = 0.9,#当误差平面趋近于平面的话加快计算速度
eval.metric = mx.metric.accuracy,#评价指标
epoch.end.callback = mx.callback.log.train.metric(100))#回调函数,观察程序运行情况
#测试
predicted <- predict(model, test_array)
predicted_labels <- max.col(t(predicted)) - 1
res<-data.frame(ImageId=seq(1:length(predicted_labels)),Label=predicted_labels)
write.csv(res,"Submission.csv",row.names = F)