opencv logPolar()和linearPolar()
logPolar是把数据从笛卡尔转到对数极坐标系,linearPolar把数据从笛卡尔坐标系转到极坐标坐标系。
说到笛卡尔坐标系到极坐标系的转换,大家并不陌生,公式如下:
设(x, y)为极坐标的一点,(![]() )为转换中心,(
)为转换中心,(![]() )为转换后的结果,则
)为转换后的结果,则
笛卡尔转到对数极坐标系的转换多了一层对数,可表示如下
这里log以自然数e为底。
接下来,首先分析一下logPolar和linearPolar输入输出参数的含义以及用法,然后给出一些实验结果。
1 logPolar()
这里把imgproc.hpp里的函数接口粘了过来,从接口说明里我们可以看到,
输入输出图像类型尺寸一致,输入参数还包括center():转换中心,M: scale 参数和flags(变换后图像插值方法)
logPolar()是这样做的转换:
I = (dx,dy) = (x - center.x,y - center.y) \\
\rho = M \cdot log_e(\texttt{magnitude} (I)) ,\\
\phi = Ky \cdot \texttt{angle} (I)_{0..360 deg} \\
M = src.cols / log_e(maxRadius) \\
Ky = src.rows / 360 \\上述说明中,除了基本的变换公式外,M和Ky这两个参数需要注意一下,这两个参数决定着变换后半径![]() 和角度
和角度![]() 的尺度,也就是说,在变换后的极坐标图像上,x、y方向上单位像素与半径
的尺度,也就是说,在变换后的极坐标图像上,x、y方向上单位像素与半径![]() 和角度
和角度![]() 的关系。
的关系。
- M决定输出图像x轴(
 )的尺度,Ky决定y轴(
)的尺度,Ky决定y轴( )的尺度。
)的尺度。 - 注意到,函数没有让我们手动设置Ky的值,Ky =
src.rows / 360已经写死,这样的话,输出极坐标图像y轴从y=0到yy=row-1的范围表示角度从0到360度的变化。
参数M没有写死,我们可以通过接口改变,那 M = src.cols / log_e(maxRadius), 代表什么意思呢, maxRadius是什么呢?
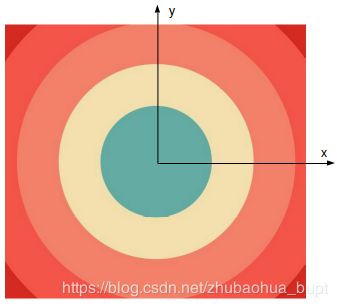
回过头来看笛卡尔向极坐标的变换,现在把输入图像看作是一个二维笛卡尔坐标系,如下图我们可以自己设定center,假设center为图像中心,那么maxRadius=![]() ,那么我们就可以看出,此时乘M的作用就是在输出图像的x轴上,將log(
,那么我们就可以看出,此时乘M的作用就是在输出图像的x轴上,將log(![]()
)从x=0拉伸到x=col-1。
笛卡尔坐标系图输入图像 对数极坐标系下图像
2 linearPolar()
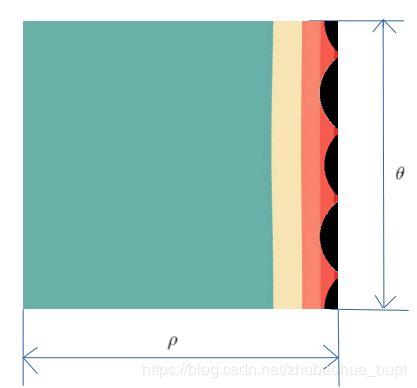
linearPolar和logPolar类似,比logPolar简单些,其变换如下图。
笛卡尔坐标系图输入图像 极坐标系下图像
3实验
下面来看几个比较特殊的实验,为了方便,用python实现:
def polar(img):
h, w = img.shape[:2]
maxRadius = math.hypot(w/2,h/2)
m = w / math.log(maxRadius)
log_polar = cv2.logPolar(img, (w/2, h/2), m, cv2.WARP_FILL_OUTLIERS + cv2.INTER_LINEAR)
linear_polar = cv2.linearPolar(img, (w/2, h/2), maxRadius, cv2.WARP_FILL_OUTLIERS + cv2.INTER_LINEAR)
cv2.imshow("log_polar",log_polar)
cv2.imshow("linear_polar",linear_polar)
cv2.waitKey(1000)
第一组: logPolar()
src m = src.cols / log_e(maxRadius) /2 m = src.cols /log_e(maxRadius)
第二组:
logPolar() linearPolar()
src m = src.cols /log_e(maxRadius) maxRadius
第三组:
logPolar() linearPolar()
src m = src.cols /log_e(maxRadius) maxRadius
- 可以想一下在这几个例子中,变换后最右侧的尖儿为什有的能连延伸到最右侧,有的不能。
- 从笛卡尔坐标系来看,这三组的src貌似形状很完美,但经过转换后可以看出后两组的瑕疵了,如果后两组也是完美对称的,那么在极坐标系下,第二组纵向应该是笔直的,第三组横行应该是平行的。