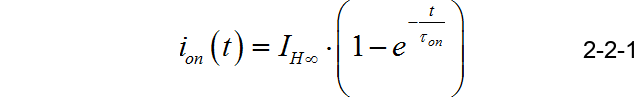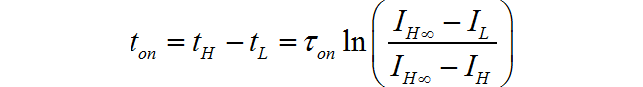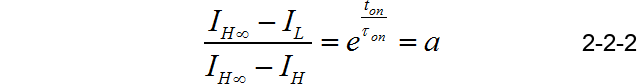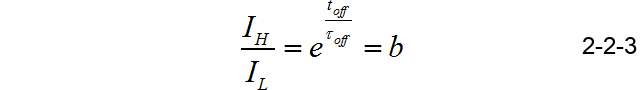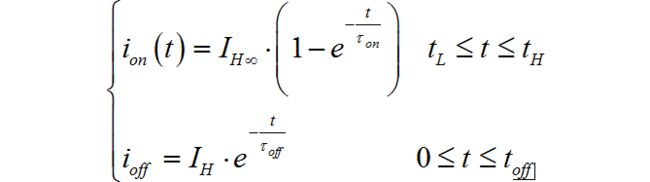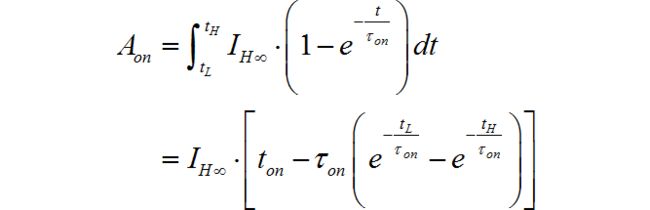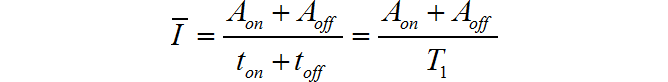磁铁驱动反向续流串接电阻的的分析

■ 电磁铁驱动

---

电磁铁对外产生的磁场与流过的电流之间，在电磁铁没有饱和之前大体呈现线性关系。如果忽略磁滞、磁饱和等非线性的特点，可以通过控制流经电磁铁的电流来控制它的电磁吸引力。

电磁铁一般可以等效成电感$L$和电阻$R$的串联。流经的稳态电流$I_0$与施加在电磁铁两端的平均电压$\bar{U}$之间的关系为：$I_0=\frac{\bar{U}}{R}$。在通常情况下，可以使用PWM来驱动电磁铁，达到很高的工作效率。

如果双极性PWM电压波形的峰值为$E_0$，PWM的占空比为${\theta }_0$，则PWM的等效平均电压为：$$U_0=E_0\left(2{\theta }_0-1\right)$$

其中${\theta }_0$的取值范围是：$\left(-1,1\right)$。

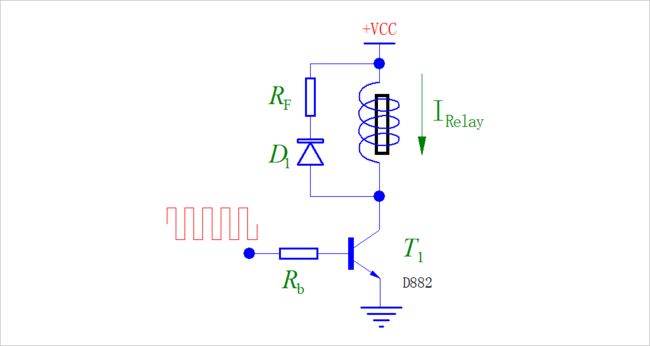
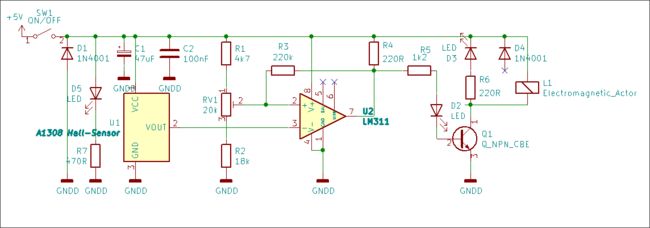
使用单管驱动电磁铁的电路比较简单，但这与使用桥电路产生双极性的PWM之间有很大的区别。电磁铁的电流在晶体管导通时，由电源电压VCC驱动下增加，在晶体管截止时通过续流二极管以及电阻Rf和R0(电磁铁的内阻)电流下降。此时流经电磁铁的电流$I_{relay}$与驱动的PWM的占空比${\theta }_0$之间就不再是一个线性关系了。

^{▲ 使用晶体管驱动电磁铁示意图}

本文通过理论分析和实验来研究，在单管驱动电磁铁的情况下：

• 流经电磁铁的电流与占空比之间的关系。
• 增加续流电阻Rf如何影响电磁铁与占空比之间的线性性。

通过这些分析，为后面使用电磁铁做控制建立下很好的数学关系和电路设计参数。

 

01实验研究

---

先通过实验研究，获得在一般情况下单管晶体管驱动电磁铁的占空比与流经电流之间的关系，然后在后面进行理论分析。

在实验中，使用 线性霍尔 器件来测量电磁铁的铁芯磁场来间接反映电流的大小。

1.实验中的元器件

(1) 功率晶体管

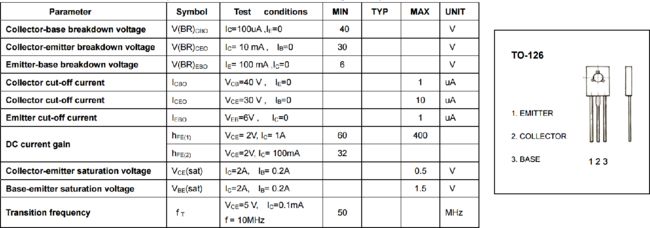
使用在 磁悬浮地球仪拆解 中拆卸下的中功率NPN晶体管 D882 作为实验中的三极管。

^{▲ D882中功率NPN三极管的主要参数}

(2) 续流二极管

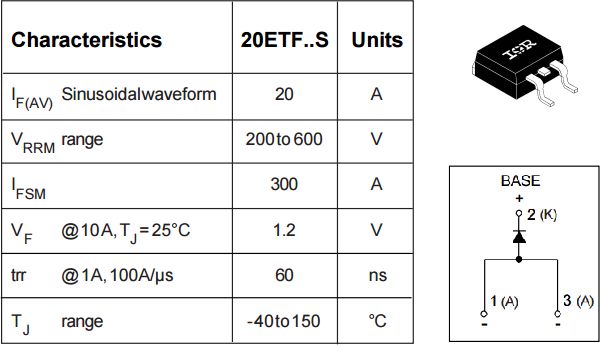
使用 20ETF06S 作为电路中的续流二极管。

^{▲ 快速恢复二极管 20ETF06S}

使用万用表测量20ETF06S的二极管前向导通电压为：0.351V。

^{▲ 电路中的两个半导体器件 | D882 , 20ETF06S}

(3) 线性HALL

使用 线性HALL 3503 测量电磁铁的磁芯磁场。

(4) 单片机板

使用 集成两路MAX1169的STC8G1K08模块，带有两路PWM输出 中的单片机实验模块所产生的PWM以及16-bitAD 转换器来测量HALL的输出。

(5) 电磁铁

使用所使用的电磁铁包括以下几种。

• 在 磁悬浮地球仪拆解 中的电磁铁和HALL框架；
• 在 使用STC8H1K28控制微型磁悬浮 中的继电器的磁铁；
• 使用一款在TB购买的 电磁铁 作为测量对象。

^{▲ 购买到的电磁铁}

• 基本参数： 电阻R=16Ω；电感（1kHz）L=13.37mH。

2.实验电路

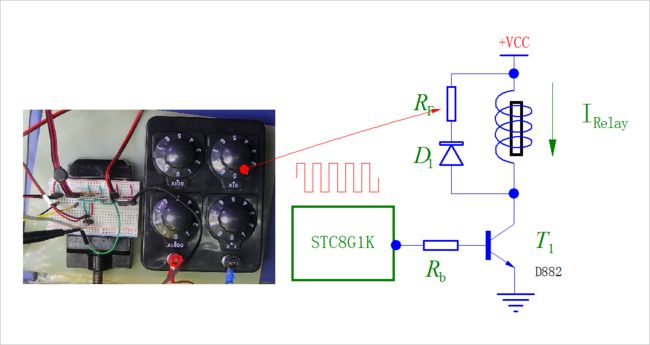
使用 低价电阻箱-阻值测试 作为R1，用于动态调整R1。在面包板上将实验电路搭建起来。

^{▲ 实验电路}

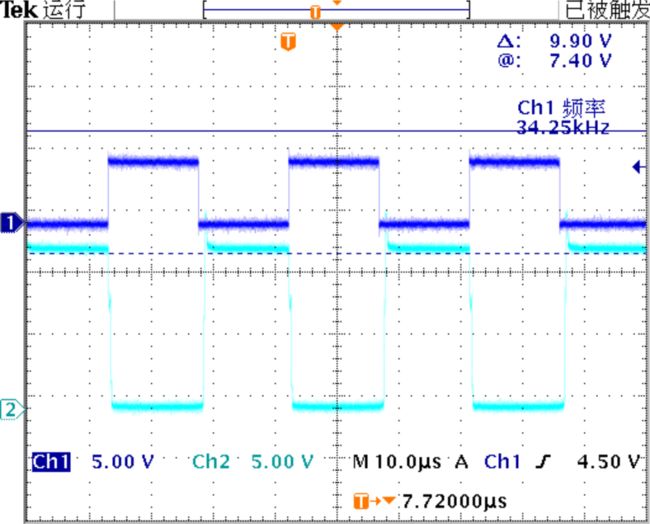
选择VCC为12V电压。测量单片机发送的PWM波形以及T1集电极电压波形如下，大体验证实验电路工作正常。

^{▲ 单片机发送的PWM波形以及T1集电极电压波形}

3.测试数据

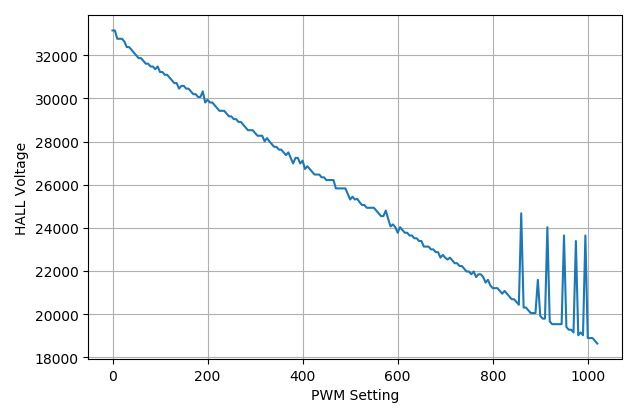
(1) 测试购买的电磁铁

• 设置R1= 0欧姆：
  ^{▲ HALL输出与PWM设置之间的关系}
• R1=10欧姆

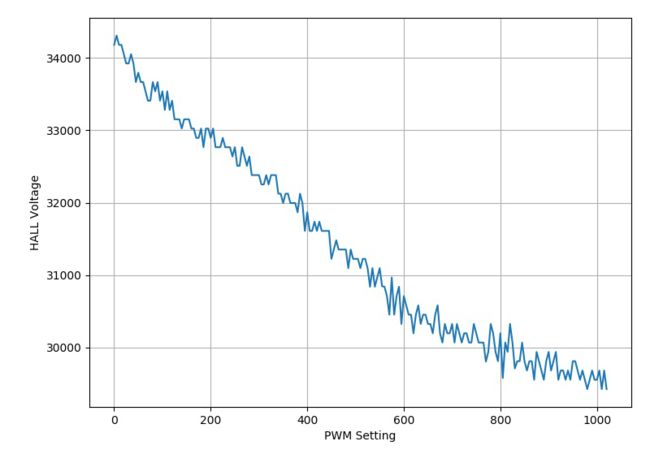
^{▲ HALL输出与PWM设置之间的关系}

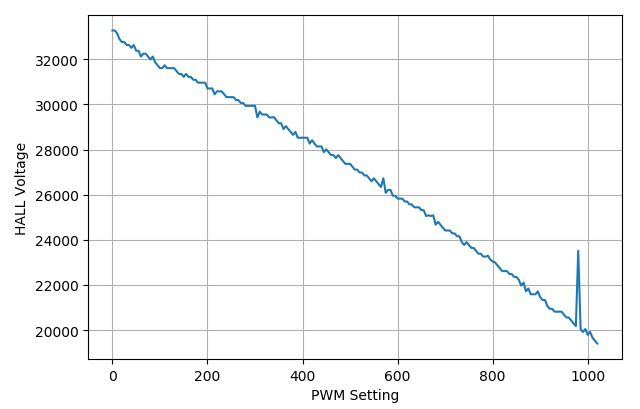
• 设置R= 100欧姆

^{▲ HALL输出与PWM设置之间的关系}

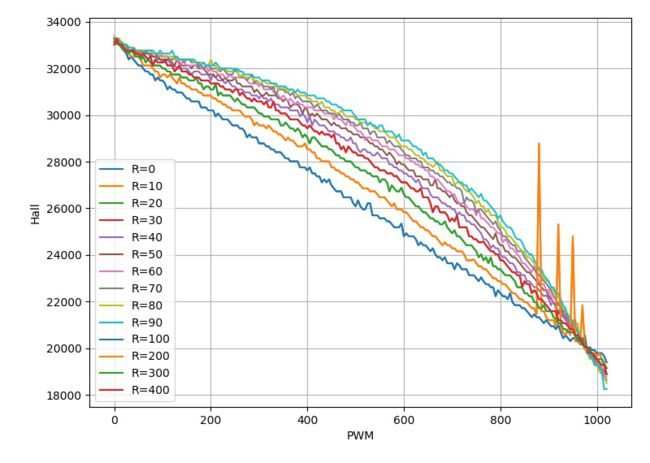
^{▲ 不同的R1对应的PWM与HALL取值之间的曲线}

(2) 测试磁悬浮地球仪电磁铁

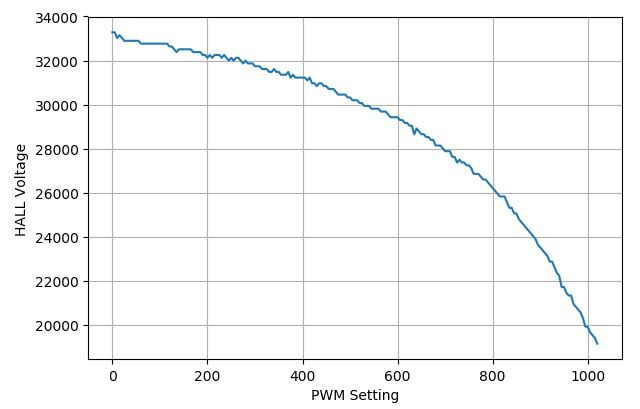
在 磁悬浮地球仪控制初步测试 中描述了磁悬浮地球仪的电磁铁以及HALL的构造。下面是测量单管驱动下占空比与HALL之间的关系。

^{▲ 单管驱动占空比与HALL输出之间的关系}

^{▲ 单管驱动占空比与HALL输出之间的关系；RF=100Ω}

 

02理论分析

---

1.分析假设

由于电路存在着很多非线性环节，它的分析根据电路不同的工作状态，所得到的结果也各有变化。下面先就一种比较简单的情况进行分析：

1. 电感中的电流始终保持连续；
2. 对于续流二极管D1，晶体管T1的导通电压假设都是0；
3. 电感等效为电感与电阻的的串联：$L_1,R_L$；
4. PWM的周期为，$T_1$，占空比为$\eta$。那么晶体管打开的时间$t_{on}$和关断时间$t_{off}$分别是：
   $$t_{on}=T_1\cdot \eta ,t_{off}=T_1\left(1-\eta \right)$$

那么电感的电流变化可以分解成两个不同的阶段：

• 晶体管导通阶段；
• 晶体管截止阶段；
  

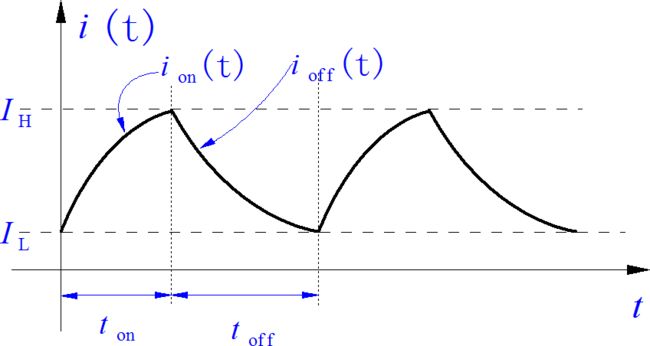
2.电流变化以及平均值

根据前面的假设，电流的变化曲线如下图所示。

^{▲ 电感中的电流变化曲线}

(1) 计算稳态下电流波动的峰值:

利用假设的简化条件，可以得到电流上升和下降的渐进稳定的电流分别是：$I_{H\infty }=\frac{V_{CC}}{R_L},I_{L\infty }=0$。可以列写出在电流上升阶段和下降阶段的对应的指数函数方程。在晶体管导通器件，电感电流指数上升：

其中：$$I_{H\infty }=\frac{V_{CC}}{R_L},{\tau }_{on}=\frac{L_1}{R_L}$$
那么

同理可得：

可知：

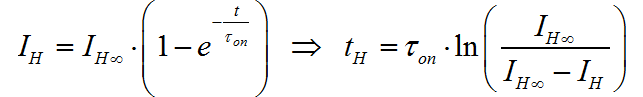
令：

分析晶体管截止的过程，可以得到：

其中时间常数：${\tau }_{off}=L_1/\left(R_1+R_L\right)$。

联合2-2-2， 2-2-3可以求解出$I_H,I_L$：

(2) 计算稳态下电流平均值

在得到$I_H,I_L,t_{on},t_{off}$的情况下，计算此时对应的电流平均值。
根据电流在上升和下降两个阶段的方程，来计算曲线的面积。

上升阶段的电流积分面积：

电流下降阶段的积分面积：

平均电流：

如果反馈续流电阻R1= 0，那么施加在的电感上的电压平均值就与占空比成正比，流经的电流与占空比之间就是线性关系。

3.数值仿真结果

根据前面实验中的条件，确定比较符合实际实验的一些参数：

• 工作电源：Vcc=12V
• 电感等效串联直流电阻：RL=16Ω
• 电感电感量：L1=13.37mH
• PWM周期：T1=1/fpwm=29.26us
• 续流串联电阻：R1从0变化到100欧姆

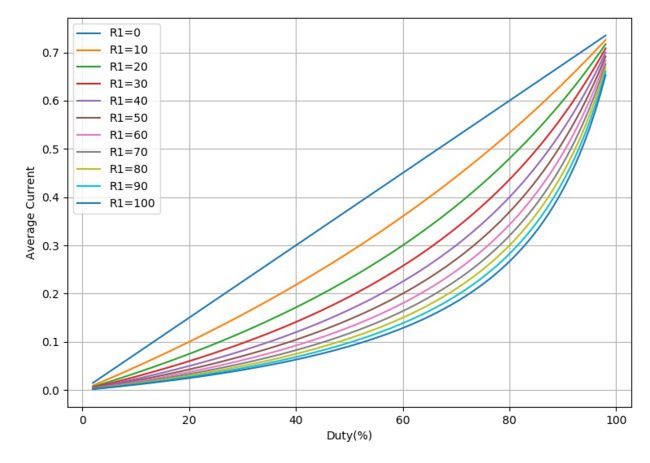
^{▲ 对于不同的R1得到的占空比与电流之间的关系}

从上图可以看到当续流二极管上串联的电阻R1=0时，流经电感电流$I_L$与占空比$\eta$之间就是一个线性关系：
$$I_L\left(\eta \right)=\frac{V_{CC}}{R_L}\cdot \eta$$

随着R1的增加，电流与占空比之间的非线性就逐步增大了。

#!/usr/local/bin/python
# -*- coding: gbk -*-
#============================================================
# SIMUL.PY                     -- by Dr. ZhuoQing 2020-07-24
#
# Note:
#============================================================

from headm import *

#------------------------------------------------------------
Vcc=12
L1=13.37e-3
RL=16.0
fpwm=34.18e3
T1=1/fpwm
R1 = 0

duty = 0.5

#------------------------------------------------------------

def CAduty(duty):
    ton = duty*T1
    toff = T1 - ton
    Ihoo =Vcc/RL
    taoon=L1/RL
    taooff = L1/(RL+R1)

    a = exp(ton/taoon)
    b = exp(toff/taooff)

    IL = (a-1)/(a*b-1)*Ihoo
    IH = b*(a-1)/(a*b-1)*Ihoo

    tH = taoon * log(Ihoo/(Ihoo - IH))
    tL = taoon * log(Ihoo/(Ihoo-IL))

    Aon = Ihoo*(ton - taoon*(exp(-tL/taoon) - exp(-tH/taoon)))
    Aoff = IH*taooff*(1-exp(-toff/taooff))

    return (Aon+Aoff)/T1

#------------------------------------------------------------

dutydim = linspace(0.02, 0.98, 100, endpoint=True)
R1Dim = linspace(0, 110, 11, endpoint=False)
printf(R1Dim)

for R1 in R1Dim:
    cadim = CAduty(dutydim)
    plt.plot(dutydim*100, cadim, label='R1=%d'%R1)

plt.xlabel("Duty(%)")
plt.ylabel("Average Current")
plt.grid(True)
plt.legend(loc='upper left')
plt.tight_layout()
plt.show()

#------------------------------------------------------------
#        END OF FILE : SIMUL.PY
#============================================================

 

※ 结论

---

• 通过实验和理论仿真分析，对于普通的电磁铁使用单管驱动时，在续流电阻接近为0的时候，流经的电流大小与单管的占空比成正比。
• 通过在续流二极管增加串联电阻，将会改变原来的线性关系。使得电流在占空比比较小的情况下上升缓慢，在占空比比较大的时候上升增加。
• 存在的疑问：那么为什么在有些设计中会在这儿增加串联电阻？比如别人下面的设计中：

^{▲ 一种简易的磁悬浮小玩意儿}