倒谱

1.       什么是倒谱？

倒谱（cepstrum)：一种信号的傅里叶变换谱经过对数运算后再进行傅里叶反变换。由于一般傅里叶谱是复数谱，因而又称复倒谱。

2.       倒频谱的数学描述

倒频谱函数CF（q）（power cepstrum）其数学表达式为：

C_F(q)= |F(logS_x(f))|²

CF(q)又叫功率倒频谱，或叫对数功率谱的功率谱，工程上常用开方形式：

C₀(q) = |F(logS_x(f))|

C₀(q)称为幅值倒频谱，有时简称倒频谱。

 

倒频谱的变量q的物理意义是什么呢？

 

为了使其定义更加明确，还可以定义：

C_y(q)= F^-1(logS_y(f))

即倒频谱定义为信号的双边功率谱对数加权，再取其傅里叶逆变换，联系一下信号的自相关函数：

R(r) = F^-1(S_y(f))

这种定义方法与自相关函数很相近，变量q与r在量纲上完全相同。

为了反映出相位信息，分离后能恢复原信号，又提出一种复倒频谱的运算方法。

 

若信号x(t)的傅立叶变换X(f)：

X(f) = X_R(f)+ iX_t(f)

若信号x(t)的倒频谱即为：

C₀(q)= F^-1(logX(f))|

显然，它保留了相位的信息。

 

那么，倒频谱与相关函数的区别是什么？

 

不同的是只差对数加权，目的是使再变换以后的信号能量集中，扩大动态分析的频谱范围和提高再变换的精度，还可以解卷积（熠积）成分，易于对原信号的分离和识别。

 

3.       倒谱分析的意义是什么？

对于高速大型旋转机械，其旋转状况是复杂的，尤其当设备出现不对中，轴承或齿轮的缺陷、油膜涡动、磨擦、质量不对称等现象时，则振动更为复杂，用一般频谱分析方法已经难于辩识(识别反映缺陷的频率分量)，而用倒频谱，则会增强识别能力。

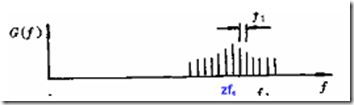
齿轮箱的振动是一种复杂的振动，如齿轮箱中轴的转速为f1，轴上齿轮的齿数z，齿轮箱的振动一定包含有f1，啮合频率z *f1 及其它们各阶谐振。

频率z*f1的等幅振动在旋转一周期间因轴的振动f1而使振幅有变化，即振幅被调制。因此，在齿轮箱振动谱图上除在频率z*f1处有谱线外，还在(z-1)f1和(z+1)f1处有谱线。考虑被f1的高次谐波调制则出现zf1的边频簇。

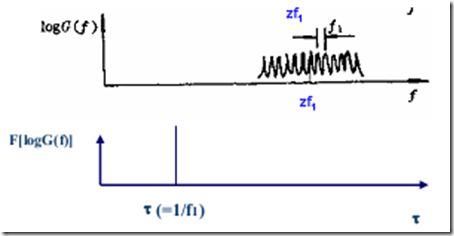
如果谱值用对数刻度则该曲线更近似周期波，其“周期”为f1。“周期”为f1的成分在齿轮故障诊断中叫故障函数，与齿轮故障有关需要识别出来。

一般齿轮箱中部有很多齿轮和转轴、因而有很不同的转轴速度和啮合频率。它们之间的相互调制使得率谱图中包含很多大小和周期都不同的周期成分，在功率谱图混在一起很难分离。

如果对具有边带信号的功率谱本身再作一次谱分析，则能把边带信号分离出来。因为功率谱图中的周期分量在第二次谱分析的谱图中是离散线段，其高度就反映原功率谱中周期分量的大小。这就是倒频谱分析。

另外，到谱分析在输入特性与系统特性的分离上也有用途。

4.       倒频谱的应用

分离信息通道对信号的影响

对数功率谱关系图

在机械状态监测和故障诊断中，所测得的信号，往往是由故障源经系统路径的传输而得到的响应，也就是说它不是原故障点的信号，如欲得到该源信号，必须删除传递通道的影响，如在噪声测量时，所测得的信号，不仅有源信号而且还有不同方向反射回来的回声信号的混入，要提取源信号必须删除回声的干扰信号。

若系统的输入为x(t)，输出为y(t)，脉冲响应函数是h(t)，

两者的时域关系为：

y(t) =x(t) * h(t)

        频域为：

               Y(f) = X(f) ·H(f) 或 S_y(f) = S_x(f) · |H(f)|²

       对上式取对数为：

logS_y(f) = logS_x(f) +log|H(f)|²

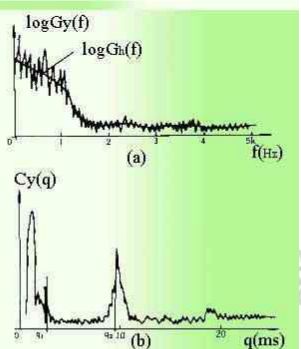
在上图中，源信号为具有明显周期特征的信号，经过系统特性logG_k(f)的影响修正，合成输出信号log_yG(f)。

 

    对上式进一步作傅里叶变换，即可得幅值倒频谱：

F(logS_y(f)) = F(logS_x(f))+ F(log|H(f)|²)

    即：

Cy(q) = C_x(q) + C_h(q)

信号在时域可以利用x(t)与h(t)的卷积求输出：在频域则变成X(f)与H(f)的乘积关系；而在倒频域则变成C_x(q) 和C_h(q)相加的关系，使系统特性C_h(q)与信号特性C_x(q)明显区别开来，这对清除通道的影响很有用处，而用功率谱处理就很难实现。

从上图来看，第二张图即相应的倒频谱图，从图中清除地表明两个组成部分：一部分为高倒频率q2，反映源信号特征；另一部分为低倒频率q1，反映系统的特性。两部分在倒频谱图上占有不同的倒频率范围，根据需要可以将信号与系统的影响分开，可以删除以保留源信号。

5.       实例

用倒频谱诊断齿故障

对于高速大型旋转机械，其旋转状况是复杂的，尤其当设备出现不对中，轴承或齿轮的缺陷、油膜涡动、磨擦、质量不对称等现象时，则振动更为复杂，用一般频谱分析方法已经难于辩识(识别反映缺陷的频率分量)，而用倒频谱，则会增强识别能力。

如一对工作中的齿轮，在实例得到的振动噪声信号中，包含着一定数量的周期分量，如果齿轮产生缺陷，则其振动或噪声信号还将大量增加谐波分量及所谓的边带频率分量。

 

什么叫边带频率，它是如何产生的？

设在旋转机械中有两个频率w1与w2存在，在这二频率的激励下，机械振动的响应呈现出周期性脉冲的拍。也就是呈现其振幅以差频（（w1 – w2）设w1 > w2）进行幅度调制的信号，从而形成拍的波形，这种调制信号是自然产生的。例如调幅波起源于齿轮啮合频率（齿轮 * 轴转数）w0的正弦载波，其幅值由于齿轮之偏心影响称为随时间而变化的某一函数S_m(t)，于是：

y(t) = S_m(t)sin(w₀t+φ)

假设齿轮轴转动频率为w_m,则可写成：

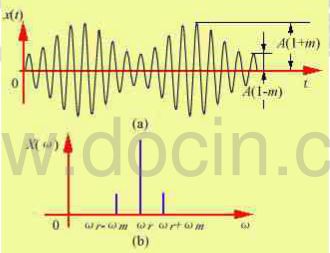
y(t) = A(1 + mcosw_mt)sin(w_mt+φ)

上图中，图a像一周期函数，但实际上它并非是一个周期函数，除非w与w成整数倍数关系，这在实际应用中，这种情况并不多见。根据三角半角关系，可写成：

y(t) = Asin n(w₀t +φ) + mA/2 sin[(w₀ + w_m)t+φ] +

mA/2 sin[(w₀ – w_m)t +φ]

不难看出，它是由w₀,(w₀ + w_m)与(w₀ - w_m)三个不同的正弦波之和，这里(w₀ + w_m)与(w₀ - w_m)之差频与和频通称为边带频率。

假如对于一个具有四个轮辐的100个齿的齿轮，其轴准转数为50转/秒。而其啮合频率5000Hz。其幅值（啮合力的大小）则由每转四次的周期为200Hz所调制（因为由四个轮辐的影响）。所以在测得的振动分量中，不仅有明显的轴转数50Hz及啮合频率（5000Hz）外，还有4800Hz及5000Hz的边带频率。

实际上，如果齿轮缺陷严重或多种故障存在，以致许多机械中经常出现的不对准、松及非线性刚度等原因，或者出现拍波截断等原因时，则边带频率将大量增加。

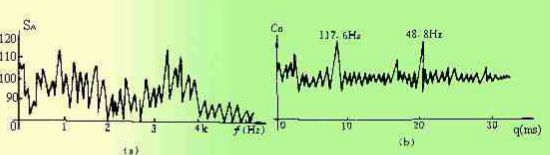
在一个频谱图上出现过多的频差，难以识别，而倒频谱则有利于识别，如下图所示，a为一个减速箱的频谱图，b为它的倒频谱图。从频谱图上清楚地看出，有两个主要频率分量：117.6Hz（85ms）及48.8Hz（20.5ms）。