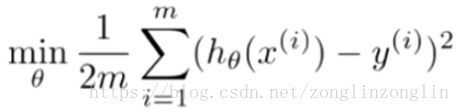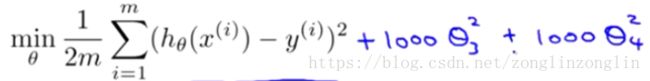卷积神经网络(1)分类注意点
几个重要的概念
1.激活函数:
非线性
一般用relu,不用sigmoid,因为sigmoid求导可能导致梯度为0.
2.softmax 函数
我们知道max,假如有两个数,a和b,并且a>b,如果取max,那么就直接取a,没有第二种可能。
但这样会造成分值小的那个饥饿。所以我希望分值大的那一项经常取到,分值小的那一项偶尔也可以取到,那么我用softmax
就可以了。现在还是a和b,a>b,如果我们按照softmax来计算取a和b的概率,那a的softmax值大于b的,所以a会经常取到,而b也会偶尔取到,概率跟他们本来的大小有关。所以说不是max,而是softmax。
定义:
假设我们有一个数组,V,Vi表示V中的第i个元素,那么这个元素的Softmax值就是
也就是说,是该元素的指数,与所有元素指数和的比值。
这个定义可以说非常的直观,当然除了直观朴素好理解之外,它还有更多的优点。例如:.计算与标注样本的差距
在神经网络的计算当中,我们经常需要计算按照神经网络的正想传播计算的分数S1,和按照正确标注计算的分数S2,之间的差距,计算Loss,才能应用反向传播。Loss定义为交叉熵:
假如有一个三分类问题,某个样例的正确答案是(1,0,0)。某模型经过softmax回归之后的预测答案是(0.5,0.4,0.1),那么这个预测和正确答案之间的交叉熵为:-(1*log0.5+0*log0.4+0*log0.1)≈0.3。如果另一个模型的预测是(0.8,0.1,0.1),那么这个预测值和真实值之间的交叉熵是:-(1*log0.8)≈0.1。从直观上就可以容易地知道第二个预测答案是要优于第一个的。通过交叉熵计算得到的结果也是一致的。
3.正则化惩罚项
防止过拟合。
(1)过拟合问题:
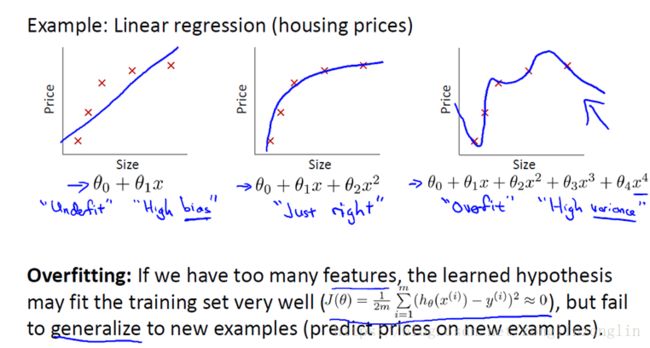
我们看预测房价这个例子,我们先对数据做线性回归,也就是左边第一张图。
如果这么做,我们可以获得拟合数据的这样一条直线,但是,实际上这并不是一个很好的模型。我们看看这些数据,很明显,随着房子面积增大,住房价格的变化趋于稳定或者说越往右越平缓。因此线性回归并没有很好拟合训练数据。
我们把此类情况称为欠拟合,或者叫做高偏差。
第二幅图,我们在中间加入一个二次项,也就是说对于这副数据我们用二次函数去拟合。自然,可以拟合出一条曲线,事实也证明这个拟合效果很好。
另一个极端是,如果在第三幅图中,叫做过拟合。
如果我们没有足够的数据集去约束这个变量过多的模型,那么就会发生过拟合。
解决方法:尽量减少选取变量的数量
正则化。减少特征变量的数量级
(2)Cost Function
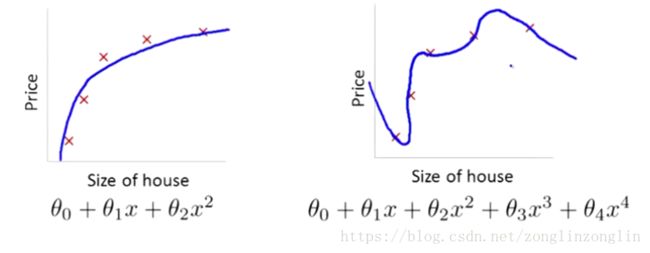
可以看出,如果用一个二次函数来拟合这些数据,那么它给了我们一个对数据很好的拟合。然而,如果我们用一个更高次的多项式去拟合,最终我们可能会得到一个过拟合曲线。
我们我们假设要加上惩罚项,从而使参数![]() 3,和
3,和![]() 4尽可能小。因为,如果你在原有代价函数的基础上加上1000乘以
4尽可能小。因为,如果你在原有代价函数的基础上加上1000乘以![]() 3这一项,那么这个新的代价函数将变得很大,所以当我们最小化这个新的代价函数的时候,我们将使
3这一项,那么这个新的代价函数将变得很大,所以当我们最小化这个新的代价函数的时候,我们将使![]() 3和
3和![]() 4接近于0,就像我们忽略了这两个值一样。
4接近于0,就像我们忽略了这两个值一样。
(2)正则化
对于房屋价格预测我们可能有上白种特征,与刚刚所讲的多项式例子不同,我们并不知道![]() 3和
3和![]() 4是高阶多项式的项。所以,如果我们有一百个特征,我们并不知道如何选择关联度更好的参数,如何缩小参数的数目等。
4是高阶多项式的项。所以,如果我们有一百个特征,我们并不知道如何选择关联度更好的参数,如何缩小参数的数目等。
因此在正则化里,我们要做的事情,就是把减小我们的代价函数所有的参数值,因为我们并不知道是哪一个或哪几个要去缩小。
L1正则化
L2正则化: