蒟蒻的树状数组解析

告知

本博客是由一个蒟蒻编写，内容可能出错，若发现请告诉本蒟蒻，以便大众阅读
转载请注明原网址：https://blog.csdn.net/LZX_lzx/article/details/107598565

树状数组和线段树

众所周知， 线段树和树状数组是兄弟来的

它们之间的关系

树状数组可以解的，线段树能解
树状数组不可以解的，线段树还是可以解
既然这样，那我学会线段树不就搞定了吗，干嘛还学树状数组呀

那么，树状数组优在何处呢？

其实呢，就是码量少，思维清晰吧
对比一下
单点修改区间查询
线段树100行起步
树状数组呢，50行左右吧
区间修改区间查询
线段树估计要飙到150了吧
树状数组依旧50行
没有对比就没有伤害呀
树状数组表示：你秀任你秀，让我上100行，难呀
这时，有些线段树忠实粉或许会思考人生：你看我还有机会吗？
机会是有的，那就是，打树状数组吧（当然有些题还是要打线段树的啦）

树状数组简介

树状数组图解

此章节内容部分引用自bestsort的小站
众所周知，一棵满二叉树长样：

挪一下位置后，变成了这样

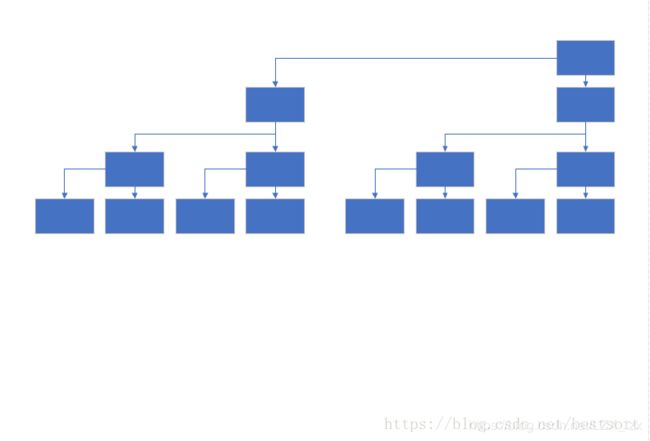
上面这个就是树状数组的画法
准确来说，这时求和数组的画法
把原数组$a$也加进来，成了这样（$c$是求和数组）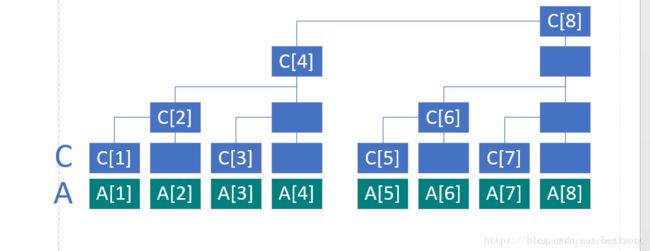
$c[i]$表示子树叶子节点的权值
如上图，有
$$\begin{gathered} c[1]=a[1] \\ c[2]=a[1]+a[2] \\ c[3]=a[3] \\ c[4]=a[1]+a[2]+a[3]+a[4] \\ c[5]=a[5] \\ c[6]=a[5]+a[6] \\ c[7]=a[7] \\ c[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8] \end{gathered}$$
转换成二进制再来看一眼
$$\begin{gathered} c[1]=c[0001]=a[1] \\ c[2]=c[0010]=a[1]+a[2] \\ c[3]=c[0011]=a[3] \\ c[4]=c[0100]=a[1]+a[2]+a[3]+a[4] \\ c[5]=c[0101]=a[5] \\ c[6]=c[0110]=a[5]+a[6] \\ c[7]=c[0111]=a[7] \\ c[8]=c[1000]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8] \end{gathered}$$
对照式子可以发现，对于一个$i$
$c[i]=a[i-2^k+1]+a[i-2^k+2]+a[i-2^k+3]\dots \dots +a[i]$（$k$为二进制下$i$第一个1前面的0的个数,例如8对应的$k$就等于3，因为$8_{10}=1000_2$，第一个1前面有3个0）
这时候，问题就来了，$2^k$怎么求？？？

引入$lowbit$

$lowbit$函数就是用来求$2^k$是多少的
具体操作是

int lowbit(int x)
{
	return x&(-x);
}

解释
“&”这个符号在C++中指的是按位与运算，具体是说，若在二进制下相同的位置两数都为1，那么&出的答案这一位也为1，否则为0
例如12&6
$$\begin{gathered} 12_{10}=1100_2 \\ {6}_{10}=0110_2（空位用0补齐） \\ ans=0110_2=6_{10} \end{gathered}$$
在上面这个数据中，12和6只有二三两个位置上才都是1，那么答案也就只有这两个位置上是1
（ 不过学树状数组的人应该都不会不知道位运算吧）
那么$x$&$(-x)$是什么意思呢
首先说明$-x$在二进制下和$x$的关系
在二进制下，$-x$就是$x$取反后再加1
例如，$10_{10}=01010_2$，那么$-10_{10}=10101_2+1_2=10110_2$（第一位是符号位）
进行按位与运算后，答案就是$00010_2=2_{10}$（第一位是符号位）
眼睛扫一扫，发现答案就是$2$
神奇吧
具体证明呢，我也不会，嘻嘻（毕竟我只是一个蒟蒻）

两个重要的子程序

一是$update$，即更新
二是$get$，即求答案

单点修改，区间查询

$update$

若要更新当前节点的$a[i]$
那么是不是可以直接更新$a[i]$的上级，$a[i]$上级的上级，以此类推
用$lowbit$到上级所在下标

void update(int now,int x)
{
	int i;
	for (i=now;i<=n;i+=lowbit(i))
		c[i]+=x;
}

$get$

对于区间查询，我们采取前缀和的求法
对于一个区间$[l,r]$，我们求出$r$的前缀和，减去$l-1$的前缀和即为答案
查询的具体过程呢，也很简单
就是从要查的节点以此往下，搜索下级
依旧是用$lowbit$

int get(int x)
{
	int i,ans;
	ans=0;
	for (i=x;i>=1;i-=lowbit(i))
		ans+=c[i];
	return ans;
}

题目

Loj130：树状数组 1 ：单点修改，区间查询

Code

#include
#include
using namespace std;
long long n,m,i,x,y,ch,c[1000005];
long long lowbit(long long x)
{
	return x&(-x);
}
void update(long long now,long long x)
{
	long long i;
	for (i=now;i<=n;i+=lowbit(i))
		c[i]+=x;
}
long long get(long long x)
{
	long long i,ans;
	ans=0;
	for (i=x;i>=1;i-=lowbit(i))
		ans+=c[i];
	return ans;
}
int main()
{
	scanf("%lld%lld",&n,&m);
	for (i=1;i<=n;i++)
	{
		scanf("%lld",&x);	
		update(i,x);
	}
	for (i=1;i<=m;i++)
	{
		scanf("%lld%lld%lld",&ch,&x,&y);
		if (ch==2) printf("%lld\n",get(y)-get(x-1));
		else update(x,y);
	}
	return 0;
}