Matlab-study-11方程式求根

Symbolic Root

syms和sym：定义/声明一个变量

syms x    %方法一
x=sym('x')    %方法二

解析解

Symbolic Root Finding: solve()

一元一次方程求解示例
求方程式$y=x•sin(x)-x$的根，即令$y=0$求 x 的值

syms x
y = x*sin(x)-x;
solve(y, x)

练习
求方程式$cos(x{)}^2-sin(x{)}^2=0$和$cos(x{)}^2+sin(x{)}^2=0$

syms x
y1 = cos(x)^2-sin(x)^2;
y2 = cos(x)^2+sin(x)^2;
z1=solve(y1,x);
z2=solve(y2,x);

二元一次方程求解示例
求解
$x-2y=5$ 且 $x+y=6$

syms x y
eq1 = x - 2*y - 5;
eq2 = x + y - 6;
A = solve(eq1,eq2,x,y)

多元方程求解示例
$a•x^2-b=0$

syms x a b
solve(a*x^2-b) 

syms x a b
solve(a*x^2-b,b) 

练习1
求解x的方程式$(x-a{)}^2+(y-b{)}^2=r^2$

syms x  y a b r
solve((x-a)^2+(y-b)^2-r^2,x) 
%%
%更好的一种写法
syms x  y a b r;
eq=(x-a)^2+(y-b)^2-r^2;
solve(eq,x)

练习2
求矩阵A的逆，其中A=[a,b;c,d]

注意：矩阵的同行元素之间用空格(或”,”)隔开;矩阵的行与行之间用”;”(或回车符)隔开。

syms a b c d;
A=[a b;c d];
inv(A)

用symbolic的方式解微分：diff()

示例
用symbolic的方式计算$y=4x^5$的微分

syms x
y = 4*x^5;
yprime = diff(y)

%对diff()的使用要注意，此处的x是symbolic的，所以，diff(y)可以求导

练习

syms x y;
f = exp(x^2)/(x^3-x+3);
g =(x^2+x*y-1)/(y^3+x+3);
fprime=diff(f)
gprime=diff(g)

用symbolic的方式解积分：int()

示例
求解

$$z=\int ydx=\int x^2{e}^{x}dx,z(0)=0$$
求得的$z=e^x(x^2-2x+2)$，
$z(x)=z(0)=e^0(0^2-2\ast 0+2)=2$,
所以需要令 $z=z-2$ 才能满足$z(0)=0$

syms x; y = x^2*exp(x);
z = int(y); 
z = z-subs(z, x, 0)

练习
求
$${\int }_0^{10}\frac{x^2-x+1}{x+3}\mathrm{d}x$$

syms x; 
y = @(x) (x.^2-x+1)./(x+3);
z = integral(y,0,10)
%不定积分用int方便，定积分用integral更方便

fsolve()

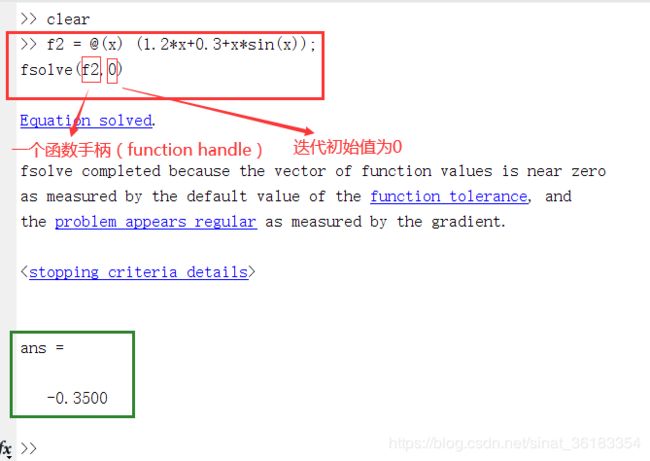
示例：解方程式

$f(x)=1.2x+0.3+x.sin(x)$
代码

f2 = @(x) (1.2*x+0.3+x*sin(x));
fsolve(f2,0)

练习

$$f(x,y)=\{\begin{array}{l}2x-y-e^{-x}\\ -x+2y-e^{-y}\end{array}$$使用初始值(x,y)=(-5,-5)

%首先定义函数root2d.m
function F = root2d(m)
F(1)=2*m(1)-m(2)-exp(-m(1));
F(2)=-m(1)+2*m(2)-exp(-m(2));
end
%将上列代码保存为函数文件，再运行下列程序

f2 = @root2d;
m0=[-5,-5];
m=fsolve(f2,m0);
x=m(1),y=m(2)

fzero()

fzero()和fsolve()很类似，两个求解的精确度一般不一样，但是fzero的一个缺点是求导可能遇到不可导点的问题，所以初始值应该小心设置，同时这个方程估计不止一个0点，所以可以同时输出fval值。

项目	多项式型	非多项式型	一维	高维
fzero()	由初值得到一个实根	由初值得到一个实根	支持	$\times$
fsolve()	由初值得到一个实根	由初值得到一个实根	支持	支持

示例

f=@(x)x.^2
fzero(f,0.1)
%结果输出NaN

fsolve(f,0)
%结果输出0.0063

f=@(x)x.^2
options=optimset('MaxIter',1e3,'TolFun',1e-10);
fsolve(f,0.1,options) %结果是1.9532e-04
fzero(f,0.1,options)%结果是NaN

求多项式解：roots()

求解
(1) $f(x)=x^5-3.5x^4+2.75x^3+2.125x^2-3.875x+1.25$

(2) $f(x)=x^3-6x^2-12x+81$

%代码
roots([1 -3.5 2.75 2.125 -3.875 1.25])

roots([1 -6 -12 81])

Numeric Root Finding Methods

Two major types:

Bracketing methods (e.g., bisection method)： 二分法：
假设值所在的区间为$[l,u]$，且$f(l)f(u)<0$

1. 循环：每次都是找$[l,u]$的中点$r=\frac{l+u}{2}$，计算$f(r)$;
2. 如果$f(r)f(u)<0$，就用 $r$ 取代原来的 $l$ ,新的x取值范围为$[r,u]$；
3. 如果$f(r)f(u)>0$，就用 $r$ 取代原来的 $u$ ,新的x取值范围为$[l,r]$；
4. 依次迭代的方式缩小范围，重复步骤1-3，直至满足停止条件5时，跳出循环
5. 停止条件：当$(u-l)<\epsilon$时，停止迭代循环
   
   

Open methods (e.g., Newton-Raphson method)牛顿法：
假设$f(x)$是连续的，且$f^{\prime }(x)$可导

1. 循环：计算$x_{n+1}=x_n-\frac{f(x_n)}{f^{\prime }(x_n)}$;
2. 依次迭代的方式缩小范围，重复步骤1-3，直至满足停止条件5时，跳出循环
3. 停止条件：当$(u-l)<\epsilon$时，停止迭代循环
   
   
   Roots are found iteratively until some criteria are satisfied:
   • Accuracy
   • Number of iteration

Recursive Functions递归函数

示例

$n!=1\ast 2\ast 3\ast ...\ast n=fact(n)$
$n!=n\ast (n-1)!=n\ast fact(n-1)$
$n!=n\ast (n-1)\ast (n-2)!=n\ast (n-1)\ast fact(n-2)$
……

function output = fact(n)
% fact recursively finds n!
	if n==1
		output = 1;
	else
		output = n * fact(n-1);
	end
end