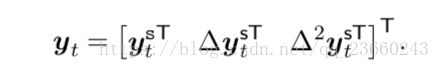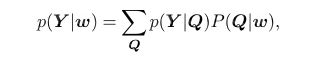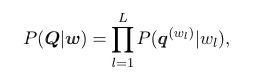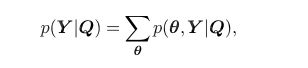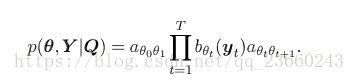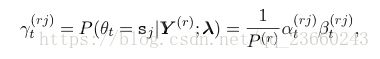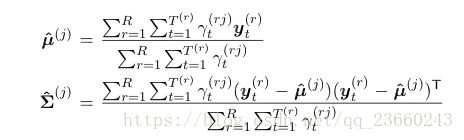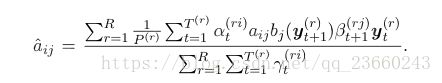基于HMM的语音识别（二）

今天进入特征提取部分，原文的2.1部分，进入正题。

特征提取阶段试图提供语音波形的紧凑形式（这里我理解不是很好，往下看）。这种形式最大限度的减少单词间的区分信息的丢失，并且与声学模型的分布假设进行良好的匹配。比如，如果对角协方差高斯分布用于状态输出分布，那么这些特征应该被设计为高斯并且是不相关的。

通常使用约25ms的重叠分析窗每10ms计算一次特征向量。其中最简单也是最常用的编码方式是梅尔倒谱系数也就是大名鼎鼎的MFCC。这些是利用截断离散余弦变换生成一个对数谱估计，该对数谱是利用平滑一个大约20个频段非线性分布的语谱的傅立叶变换得到的。非线性的频率范围通常被称之为梅尔范围（mel scale），他很逼近人耳的响应。DCT之所以被利用是为了平滑谱估计并且对特征元素去相关。经过余弦变换，第一个元素表示频带的对数能量平均值。这有时会被帧的对数能量所取代，或者完全删除。

进一步的约束被嵌入到感知线性预测（PLP）中。PLP根据感知加权的非线性压缩功率谱来计算线性预测系数，然后将线性预测系数转换为倒谱系数。PLP根据感知加权的非线性压缩功率来计算线性预测系数，然后将线性预测系数转换为倒谱系数。在实际应用中，PLP比MFCC在嘈杂的环境里有更好的表现，所以PLP一般是更好的编码方式。

除了倒谱系数以外，一阶和二阶回归系数通常也被添加到启发式的尝试中，以补偿由基于HMM的声学模型产生的条件独立性假设。如果原始的特征向量为yt^s,那么delta参数为：

其中n是窗口长度，wi是回归系数。delta-delta系数同理，当我们把上述放在一起时候如下：

最后的结果是一个大约40维度的特征向量，他们平行但是不是完全相互独立。

【PS：这段其实说的并不是很仔细，或者很清楚，因为MFCC其实是一个大的专题，并不是这一两句能说清楚的，我日后如果有机会会做一篇MFCC的文章，并且把程序写出来放到git，这里暂且先这么认为，我们在梳理】

HMM声学模型

正如我们前面所说的，我们说的每个单词wk都可以分解为Kw个基本因素的序列。这个序列我们称之为发音：

为了适应多重发音的这种情况，我们可以通过多重发音来计算相似度p(Y|w)：

这里的求和是对w所有可能的发音的序列求解的，Q是特定发音的序列：

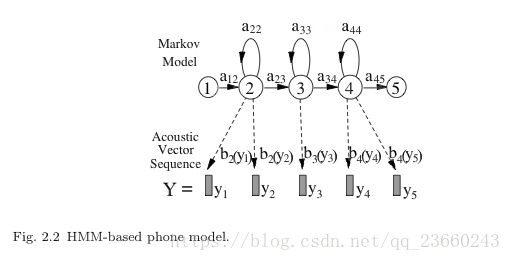
但是事实上，wl的不同发音仅很少个数，对于上述式子的追踪还是很容易的。每一个因素q都被一个连续密度的HMM模型所描述，如下：

aij表示转移概率，bj()表示输出的观测分布。在运行的时候，一个HMM模型在每个时间步长上使得从一个状态转移到另一个状态，那么这个特殊的从si到sj状态转移的概率就是aij。进入一个状态后，通过进入状态的概率分布得到特征向量，而这个分布就是bj()。这种处理的形式产生标准的条件不相关的假设：

1. 在知道前一个状态的前提下，本状态和其他状态都是相互条件独立的。

2. 在给定生成观测序列的状态的前提下，观测序列都是条件独立的。

目前为止，单多变量高斯模型的分布假设如下：

其中u是状态sj的均值，累加符号是他的协方差。由于声音矢量y的维数相当大，我们的协方差经常约定为对角的。在后面的HMM Structure Refinements,我们将会讨论混合高斯模型的好处。

给定我们的合成物Q同时把所有的基础音素串联，我们可以得到声音相似度如下：

其中sita是状态的序列，展开后者：

其中sita0和sitaT+1表示输入和输出状态。

声音模型的参数：

本参数可以通过使用前后向算法在训练数据上高效的被估计出来，比如期望最大。对于每个语音来说Y^r,r=1....R,在语音中对应词序列的HMM被找到，并且综合HMM被构建。在算法的第一阶段，E-step，前向概率为：，后向概率为：，他们分别通过如下的迭代被算出：

对于长语音上面的式子可能会发生下溢，所以改成log概率去避免这个问题。

在给定前向和后向概率的情况下，在t时刻给定语音r的模型状态在sj的概率为：

其中这些状态的占有概率，也称作占有数量，他们表明了数据和模型状态的软对齐。新的高斯参数被定义如下：

他们是通过给出前面对齐的情况下最大化相似度来得到的。一个相似的重估方程为转移概率诞生：

这是算法的第二或者第M步。从一些初始化的参数开始，通过EM算法连续的产生参数集：，这能保证把相似度提高到局部最大。一个较为通用的做法是把初始高斯分布参数集设置为全局数据的均值和方差，并且设置所有的转移概率都相等，这就被称作：flat start模型。

这种声学建模的方式通常称之为 beads-on-a-string（表面译为串成一串的珠子），之所以这么叫是因为语音发音完全被音素模型的序列串联表示。这种方式最大的缺点在于把每个词汇分解成上下文独立的基本音素很难捕获那些在实际语音中上下文相关的变量。打个比方，mood和cool两个词语的基本发音都是相同的元音“oo”，然而在实际中，由于oo前后的环境不同，其实现可能是非常不同的。我们叫上下文独立的音素模型为monophones，也就是单因素模型。

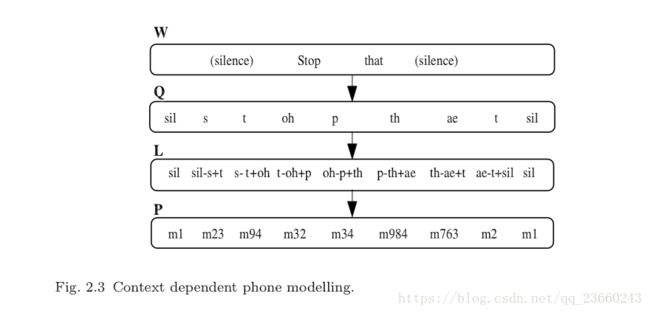
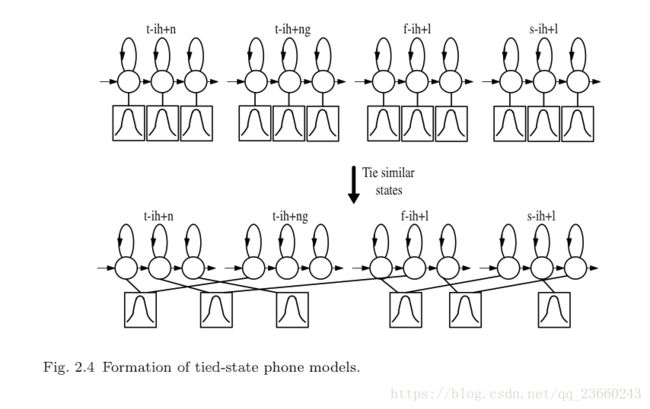
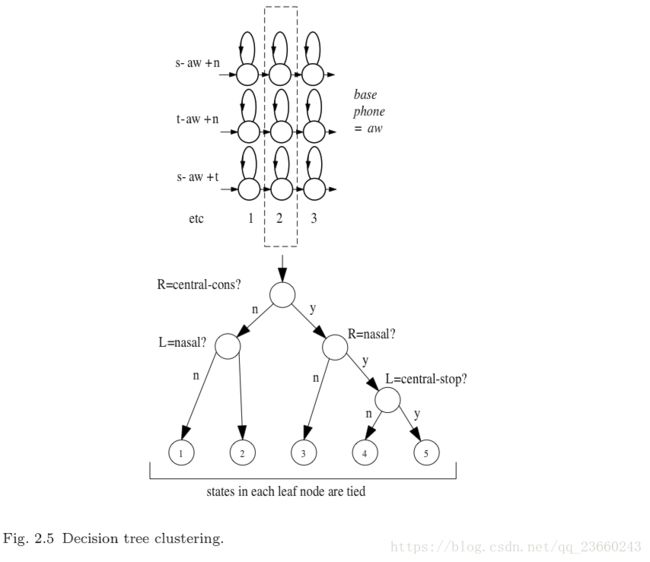
一个简单的弥补这个问题的办法就是把每个音素的左右两个音素对也进行建模。我们把这种声学建模称之为triphone（三音素），如果有N个基本音素，那么有N^3个潜在三音素（三个位置，每个位置N中可能，自己算一下）。为了避免结果数据发散（sparsity，对于这个我理解还不是很好，暂时把它看做对结果有坏影响的情况），逻辑上三音素的完整集合L可以通过分类然后把每个类的结果拿出从而得到一个实际的P个三音素模型（这里可以推断，P

而参数状态绑定如下图：

其中x-q+y表示音素q的上下文：前一个音素为x，后一个音素为y。每一个基本音素的发音q都是参照发音词典，然后根据上下文被映射成为逻辑上的音素，然后这些逻辑上的音素最终被映射成为物理上的模型。注意跨越单词边界的上下文依赖，这对于捕获很多语音过程都很重要。比如在stop that中的p，在接下来的辅音被突然抑制。

之所以我们把逻辑到现实模型的分类放在状态层次而不是模型层次是因为：相较于后者前者更加简单，同时能健壮的估计出更多的模型。关于状态绑定一般的选择都是选用决策树算法。每个音素q的每个状态都有一个二叉树与它关联。树的每个节点都携带者关于上下文的问题，为了分类音素q的状态i，所有音素q的模型中的所有状态i被划分到一个pool中，并且处在树的根节点。依赖于每个节点问题的答案，状态池被连续切分直到变成叶子节点。每个叶子节点的所有状态被绑定形成一个物理模型。在给定最终状态绑定的情况下，最大化训练数据相似度的问题通过从预定义的集合中选取（PS：这句想了好久，不知道如何翻译最完美，放上原文：The questions at each node are selected from a predetermined set to maximise the likelihood of the training data given the final set of state-tyings）。如果状态的输出分布是单高斯并且状态的occupation counts知道的情况下，那么我们可以在不使用训练数据的情况下，可以很容易的在任何节点通过切分高斯来增加相似度。所以说，使用贪婪迭代的节点切分算法，决策树的成长将会非常高效。下图说明了此算法：

在途中，逻辑音素s-aw+n和t-aw+n被分配给了叶子节点3，所以在实际的模型中，他们分享相同的状态。

使用音素驱使的决策树来划分状态有很多好处，特别是，在训练数据的时候所需但却看不到的逻辑模型很容易被合成。一个缺点是分类可能会很粗糙，这个问题可以通过称之为soft-tying 的方法削减。在这种框架下，一个后处理阶段用来分组每个状态和他相邻的两个状态，并且汇集他们的高斯模型。因此，单高斯模型转换成了混合高斯模型，但同时又保持了系统的高斯模型数量不变。

总结一下，目前语音识别的声学建模的核心由绑定三个状态的HMM模型集合，模型的输出概率分布为高斯分布。主要步骤概括如下：

1. 单音素高斯HMM模型被创建，模型的均值和方差等于训练数据的均值和方差，也称作flat-start。

2. 单音素高斯模型的参数通过步骤3或者步骤4的EM迭代被估计。

3. 每一个单高斯单音素q对于训练数据集中的每个不同的triphone x-q+y都拷贝复制一份。

4. 最终的训练数据的结果集triphones被EM算法又重新估计一遍，同时最后一次state occupation counts被记录下来。

5. 对于每个音素中的每个状态创建一个决策树，训练数据的triphones被映射为一个数量更少的绑定triphones，同时用EM算法迭代重估计。

最终结果是所需要的绑定状态的依赖于上下文的升学模型集。

PS:其实这一张感觉难点不少，初次看有很多不明白的地方，我只能强制自己先试图理解，然后后面的章节如果有可能把这里的坑解决，或者干脆另外写一个博客解释这里的问题，希望对大家有帮助。