ADP(自适应动态规划)-HDP
ADP
自适应动态规划(Adaptive/Approximate Dynamic Programming,ADP)是在动态规划的基础上发展起来的,最早由 Paul J. Werbos 提出。ADP 的模型框架有:启发式动态规划(Heuristic Dynamic Programming,HDP),双启发式动态规划(Dual Heuristic Programming,DHP)、全局双启发式动态规划(Globalized Dual heuristic Programming,GDHP)以及将模型网络和评价网络合并形成的 ADHDP,ADDHP, ADGDHP 三种动作依赖(Action-Dependent)的 ADP 模型。在 DHP,HDP,GDHP 中,有评价网络(Critic Network)、模型网络(Model Network)和执行网络(Action Network)。在 ADHDP,ADDHP,ADGDHP 仅有执行网络(Action Network)和评价网络(Critic Network)。
ADP 的基本框架下图所示,这与强化学习中的 Actor-Critic 框架是一致的。
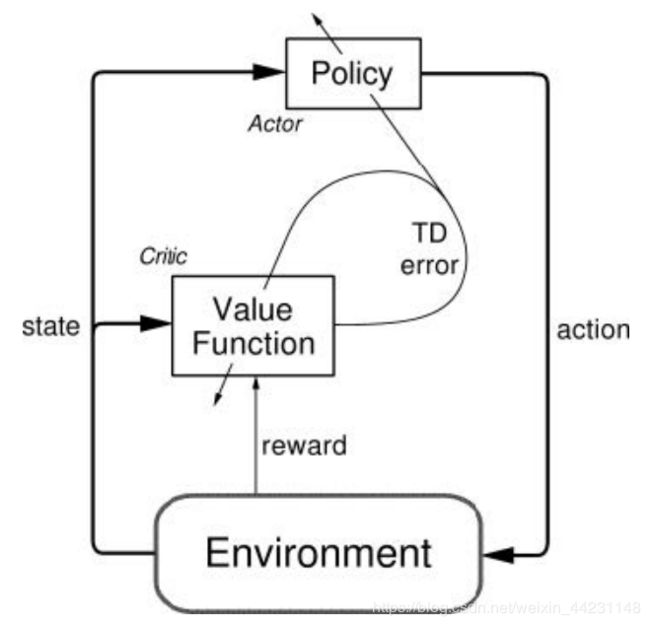
此次来讲一下ADP中的HDP。
HDP原理
HDP采用Acotr-Critick框架,框图如下图所示:
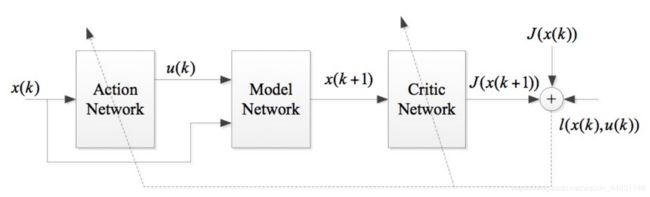
模型中共有3个网络,评价网络(Critic Network)、模型网络(Model Network)和执行网络(Action Network)。评价网络(Critic Network)的输入为状态 x ( k + 1 ) x(k+1) x(k+1),输出为 J ( x ( k + 1 ) ) J(x(k+1)) J(x(k+1)),用来计算状态的性能指标(类似RL中的价值函数V);模型网络(Model Network)用来逼近当前的系统;执行网络(Action Network)输入为状态 x ( k ) x(k) x(k),输出为 u ( k ) u(k) u(k),用来选择当前的输入(类似RL中的Action)。
损失函数定义为:
L o s s = 1 2 e 2 (1) Loss=\frac{1}{2}e^2\tag{1} Loss=21e2(1)
e = J ^ ( x ( k + 1 ) ) − J ( x ( k + 1 ) ) (2) e = \hat{J}(x(k+1))-J(x(k+1))\tag{2} e=J^(x(k+1))−J(x(k+1))(2)
其中, J ^ ( x ( k + 1 ) ) \hat{J}(x(k+1)) J^(x(k+1))为Critic Network的实际输出。 J ( x ( k + 1 ) ) J(x(k+1)) J(x(k+1))为Label。根据贝尔曼最优方程:
J ( x ( k + 1 ) ) = J ( x ( k ) ) − l ( x ( k ) , u ∗ ( k ) ) (3) J(x(k+1))= J(x(k))-l(x(k),u^*(k))\tag{3} J(x(k+1))=J(x(k))−l(x(k),u∗(k))(3)
u ∗ ( k ) u^*(k) u∗(k)表示在状态为 x ( k ) x(k) x(k)时选取的最优输入(动作)。有了损失函数,则可以对Critic Network和Action Network进行更新了。对于Model Network,是对系统的逼近,因此,我们首先需要训练Model Network,Model Network训练完成后保持不变,接着训练Critic Network和Action Network。
代码实现
例子
假设非线性系统模型:
x k + 1 = g ( x k ) f ( x k ) + u k (4) x_{k+1}=g(x_k)f(x_k)+u_k\tag{4} xk+1=g(xk)f(xk)+uk(4)
其中:
f ( x k ) = [ 0.2 x k ( 1 ) e x k 2 ( 2 ) 0.3 x k 3 ( 2 ) ] (5) f(x_k)=\left[ \begin{array}{ccc} 0.2x_k(1)e^{x_k^2(2)} \\ 0.3x_k^3(2) \end{array} \right]\tag{5} f(xk)=[0.2xk(1)exk2(2)0.3xk3(2)](5)
g ( x k ) = [ 0 − 0.2 ] (6) g(x_k)=\left[ \begin{array}{ccc} 0 \\ -0.2 \end{array} \right]\tag{6} g(xk)=[0−0.2](6)
性能指标:
J = 1 2 ∫ 0 ∞ ( x T ( t ) Q ( t ) x ( t ) + u T ( t ) R ( t ) u ( t ) ) d t (7) J=\frac{1}{2}\int_{0}^{\infty}(x^T(t)Q(t)x(t)+u^T(t)R(t)u(t))dt\tag{7} J=21∫0∞(xT(t)Q(t)x(t)+uT(t)R(t)u(t))dt(7)
其中, x 1 ∈ [ − 2 , 2 ] x_1 \in[ -2,2] x1∈[−2,2] , x 2 ∈ [ − 1 , 1 ] x_2 \in[-1,1] x2∈[−1,1],初始状态为 x ( 0 ) = [ 2 , − 1 ] x(0)=[2,-1] x(0)=[2,−1],Q和R取单位矩阵。
代码
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
import numpy as np
state_dim = 2 # 状态维度
v_dim = 1 # 价值维度
action_dim = 1 # 动作维度
A_learing_rate = 0.01 # A网络学习率
V_learing_rate = 0.01 # V网络学习率
learing_num = 1000 # 学习次数
sim_num = 20 # 仿真步长
x0 = np.array([2,-1]) # 初始状态
epislon = 0.01 # 阈值
model_net_train_num = 50 # 模型网络训练测次数
torch.manual_seed(1) # 设置随机种子,使得每次生成的随机数是确定的
# 采样状态 将状态定义在x1 [-2,2] x2 [-1,1]
x = np.arange(-2, 2, 0.1)
y = np.arange(-1, 1, 0.1)
xx, yy = np.meshgrid(x, y) # 为一维的矩阵
state = np.transpose(np.array([xx.ravel(), yy.ravel()])) # 所有状态
state_num = state.shape[0] # 状态个数
####################################################################################################################
# 定义原始模型函数
####################################################################################################################
def model(current_state, u):
next_state = np.zeros([current_state.shape[0], current_state.shape[1]]) # 初始化下一个状态
for index in range(current_state.shape[0]): # 对每个样本计算下一个状态 根据输入的u
next_state[index, 0] = 0.2 * current_state[index, 0] * np.exp(current_state[index, 1] ** 2)
next_state[index, 1] = 0.3 * current_state[index, 1] ** 3 - 0.2 * u[index]
pass
return next_state
# 动作采样 将输入定在[-10 10] 内
action = np.arange(-10, 10, 0.05)
action_num = action.shape[0]
# 计算状态-动作对
a = np.random.rand(4,2)
b = np.random.rand(3)
state1 = np.repeat(state,action.shape[0],axis=0)
action1 = np.tile(action,(state.shape[0],1)).reshape((-1,1))
model_input = np.zeros([state.shape[0]*action.shape[0],2+1])
model_input[:,0:2] = state1
model_input[:,2] = action1.reshape(state.shape[0]*action.shape[0])
# 计算模型网络的label
model_target = model(state1,action1)
########################################################################################################################
# 定义神经网络类
########################################################################################################################
class Net1(torch.nn.Module):
# 初始化
def __init__(self):
super(Net1, self).__init__()
self.lay1 = torch.nn.Linear(state_dim, 10, bias = False) # 线性层
self.lay1.weight.data.normal_(0,0.5) # 权重初始化
self.lay2 = torch.nn.Linear(10, action_dim, bias = False) # 线性层
self.lay2.weight.data.normal_(0, 0.5) # 权重初始化
def forward(self, x):
layer1 = self.lay1(x) # 第一隐层
layer1 = torch.nn.functional.relu(layer1,inplace= False) # relu激活函数
output = self.lay2(layer1) # 输出层
return output
class Net2(torch.nn.Module):
# 初始化
def __init__(self):
super(Net2, self).__init__()
self.lay1 = torch.nn.Linear(state_dim+action_dim, 10, bias = False) # 线性层
self.lay1.weight.data.normal_(0,0.5) # 权重初始化
self.lay2 = torch.nn.Linear(10, state_dim, bias = False) # 线性层
self.lay2.weight.data.normal_(0, 0.5) # 权重初始化
def forward(self, x):
layer1 = self.lay1(x) # 第一隐层
layer1 = torch.nn.functional.relu(layer1,inplace = False) # relu激活函数
output = self.lay2(layer1) # 输出层
return output
########################################################################################################################
# 定义价值迭代类
########################################################################################################################
class HDP():
def __init__(self):
self.V_model = Net1() # 定义V1网络
self.A_model = Net1() # 定义A网络
self.modelnet = Net2() # 定义模型网络
self.criterion = torch.nn.MSELoss(reduction='mean') # 平方误差损失
# 训练一定次数,更新Critic Net的参数
# 这里只需要定义A网络和V2网络的优化器
self.optimizerV = torch.optim.SGD(filter(lambda p: p.requires_grad, self.V_model.parameters()), lr = V_learing_rate) # 利用梯度下降算法优化model.parameters
self.optimizerA = torch.optim.SGD(filter(lambda p: p.requires_grad, self.A_model.parameters()), lr = A_learing_rate) # 利用梯度下降算法优化model.parameters
self.optimizer_model = torch.optim.SGD(self.modelnet.parameters(), lr=0.01) # 利用梯度下降算法优化model.parameters
self.learn_model() # 训练模型网络
self.cost = [] # 初始化误差矩阵
# for p in self.V_model.parameters():
# p.requires_grad = True # 固定模型网络参数
# pass
# print('Model Net Training has finished!')
# for p in self.A_model.parameters():
# p.requires_grad = True # 固定模型网络参数
# pass
# print('Model Net Training has finished!')
# pass
def learn_model(self):
print('Model Net Training has begun!')
self.model_loss = []
for learn_index in range(model_net_train_num): # 训练模型
model_predict = self.modelnet(Variable(torch.Tensor(model_input))) # 预测值
loss = self.criterion(model_predict, Variable(torch.Tensor(model_target))) # 计算损失
self.model_loss.append(loss)
#print('loss: ', np.array(loss.data))
if np.abs(loss.data) < 0.001:
break
self.optimizer_model.zero_grad() # 对模型参数做一个优化,并且将梯度清0
loss.backward(retain_graph=True) # 计算梯度
self.optimizer_model.step() # 权重更新
pass
print('Model Net Training has finished!')
pass
####################################################################################################################
# J_loss函数
####################################################################################################################
def J_loss1(self,sk,uk):
Vk = np.zeros(sk.shape[0]) # x_k 的V值
for index in range(uk.shape[0]): # 对每个样本计算下一个状态 根据输入的u
Vk[index] = sk[index,0] ** 2 + sk[index,1] ** 2 + uk[index] ** 2
pass
return Vk
pass
def J_loss2(self,sk,uk,Vk_1):
Vk = np.zeros(uk.shape[0]) # x_k 的V值
for index in range(uk.shape[0]): # 对每个样本计算下一个状态 根据输入的u
Vk[index] = sk[index,0] ** 2 + sk[index,1] ** 2 + uk[index] ** 2 + Vk_1[index,0]
pass
return Vk
pass
def fitparas(self,p1,is_required):
if is_required==1:
for p in p1.parameters():
p.requires_grad = True # 固定模型网络参数
pass
else:
for p in p1.parameters():
p.requires_grad = False # 固定模型网络参数
pass
pass
####################################################################################################################
# 定义学习函数
####################################################################################################################
def learning(self):
self.loss = []
for train_index in range(learing_num):
print('the ' , train_index + 1 , ' --th learing start')
u_star = np.zeros([state_num, 1])
for index in range(state_num): # 循环计算所有状态的U*
st = model_input[(index)*action_num:(index+1)*action_num,:]
#print(st)
new_xk_1 = self.modelnet(Variable(torch.Tensor(st)))
next_V1 = self.V_model(Variable(torch.Tensor(new_xk_1)))
A1 = self.J_loss2(st, action, np.array(next_V1.data))
u_star_index = np.argmin(A1)
u_star[index] = action[u_star_index]
pass
# 计算target
Vk = self.V_model(Variable(torch.Tensor(state))) # 计算Vk
Gd = self.J_loss1(state , u_star) # 计算gD
target = np.array(Vk.data).reshape(Vk.shape[0],1)-np.array(Gd).reshape(Vk.shape[0],1) #计算标签
# 计算预测值 # 这里需要对两个网络A和V网络计算loss 两个loss是一样的
# 但是因为A网络需要经过Model网络计算梯度,不能直接中间结果保存到某个变量中,再带入另一个net 这样会出现 梯度为 None
# 具体的操作如 predict1
# 开始有用predict1 直接对V网络计算梯度,但是好像报了一个关于Pytorch版本的错误 然后 就利用中间变量保存
#model_input_with_u = Variable(torch.Tensor(np.zeros([state_num,state_dim+action_dim])))
model_input_with_u = torch.randn(state_num, state_dim + action_dim)
#model_input_with_u[:,0:state_dim] = Variable(torch.Tensor(state))
model_input_with_u[:,0:state_dim] = torch.tensor(state).type(torch.FloatTensor)
model_input_with_u[:,state_dim] = self.A_model(Variable(torch.Tensor(state))).view(state_num).type(torch.FloatTensor)
next_xk_1 = self.modelnet(Variable(torch.Tensor(model_input_with_u))).type(torch.FloatTensor)
predict2 = self.V_model(Variable(torch.Tensor(next_xk_1))) # 计算Vk+1
predict1 = self.V_model(\
self.modelnet(\
torch.cat((Variable(torch.tensor(state)).type(torch.FloatTensor),\
self.A_model(Variable(torch.Tensor(state))).view(state_num,1).type(torch.FloatTensor)\
),1)
)
)
# predict2 = self.V_model( \
# self.modelnet( \
# torch.cat((Variable(torch.tensor(state)).type(torch.FloatTensor), \
# self.A_model(Variable(torch.Tensor(state))).view(state_num, 1).type(torch.FloatTensor) \
# ), 1)
# )
# )
# for tt in range(next_xk_1.shape[0]):
# for ttt in range(next_xk_1.shape[1]):
# next_xk_1[tt,ttt].requires_grad = True
# pass
# pass
#
# for t in range(predict.shape[0]):
# predict[t].requires_grad = True
#print('是否求梯度', next_xk_1[5,1].requires_grad)
#############################################################################################################
# 更新Crictic Actor网络
#############################################################################################################
# for p in self.A_model.named_parameters():
# p.requires_grad
#self.fitparas(self.A_model, 1)
#self.fitparas(self.V_model, 0)
#self.fitparas(self.modelnet, 0) # Medel Net 不更新
# A_loss = self.criterion(self.A_model(Variable(torch.Tensor(state))).view(state_num,1),Variable(torch.Tensor(target))) # 计算损失
A_loss = self.criterion(predict1,torch.tensor(target).type(torch.FloatTensor)) # 计算损失
#A_loss.requires_grad = True
self.optimizerA.zero_grad() # 对模型参数做一个优化,并且将梯度清0
A_loss.backward(retain_graph=True) # 计算梯度
self.optimizerA.step() # 权重更新
print(' the ', train_index + 1, ' Action Net have updated')
# for name, parms in self.A_model.named_parameters():
# print('A_model-->name:', name, '-->grad_requirs:', parms.requires_grad, \
# ' -->grad_value:', parms.grad)
# self.fitparas(self.V_model, 1) # 只对V求梯度
# self.fitparas(self.A_model, 0)
#self.fitparas(self.modelnet, 0)
V_loss = self.criterion(predict2, Variable(torch.Tensor(target))) # 计算损失
self.optimizerV.zero_grad() # 对模型参数做一个优化,并且将梯度清0
V_loss.backward(retain_graph=True) # 计算梯度
self.optimizerV.step() # 权重更新
print(' the ' , train_index+1 , ' Critic Net have updated')
# for name, parms in self.V_model.named_parameters():
# print('V_model-->name:', name, '-->grad_requirs:', parms.requires_grad, \
# ' -->grad_value:', parms.grad)
# print('A paras:\n', list(self.A_model.named_parameters()))
# print('V paras:\n', list(self.V_model.named_parameters()))
# print('model paras:\n', list(self.modelnet.named_parameters()))
print(" AC net loss: ",A_loss.data)
self.loss.append(np.array(A_loss.data))
# 保存和加载整个模型
# 每次训练完可以保存模型,仿真时候 直接load训练好的模型 或者 继续训练可以接着上一次训练的结果继续训练
#torch.save(model_object, 'model.pth')
#model = torch.load('model.pth')
pass
#######################################################################################################
# 定义仿真函数
# 通过得到的Actor选择动作
# 同时利用Critic计算V
#######################################################################################################
def simulator(self):
print('the simulation is start')
#self.restore(self.path)
State_traject = np.zeros([sim_num + 1, state_dim])
State_traject[0, :] = x0
u_traject = np.zeros([sim_num, 1])
for index in range(sim_num):
print('the ', index, ' --th time start')
print('当前状态:', Variable(torch.Tensor(State_traject[index,:])).data)
sim_actor = self.A_model(Variable(torch.Tensor(State_traject[index,:])))
print('当前输入:',sim_actor)
u_traject[index] = sim_actor.data
sim_nexstate = model(State_traject[index, :].reshape(1, 2), sim_actor.data) #带入实际系统中
print('下一时刻状态:', sim_nexstate)
State_traject[index + 1, :] = sim_nexstate
pass
pass
V_traject = self.V_model(Variable(torch.Tensor(State_traject))).data
print('the simulation is over')
self.plot_curve(State_traject , u_traject , V_traject , self.loss,self.model_loss)
pass
#######################################################################################################
# 绘图函数
# 分别绘制状态轨迹 控制输入u轨迹 值函数V轨迹
# 并将结果保存!
#######################################################################################################
def plot_curve(self, s, u, V,cost,modelloss):
# print('\nstate\n',s)
# print('\nu\n', u)
# print('\nV\n', V)
# 绘制状态轨迹
plt.figure(1)
plt.plot(s[:, 0], 'r', label='State_1')
plt.plot(s[:, 1], 'b', label='State_2')
plt.title('State_Trajecteory')
plt.xlabel('iter')
plt.ylabel('State')
plt.legend()
plt.grid()
plt.savefig(r'ADPresultfig\HDP_state.png')
plt.show()
# 绘制控制输入u轨迹
plt.figure(2)
plt.plot(u, )
plt.title('U_Trajecteory')
plt.xlabel('iter')
plt.ylabel('u')
plt.grid()
plt.savefig(r'ADPresultfig\HDP_u.png')
plt.show()
# 绘制值函数V的轨迹
plt.figure(3)
plt.plot(V, 'r')
plt.title('V_Trajecteory')
plt.xlabel('iter')
plt.ylabel('V')
plt.grid()
plt.savefig(r'ADPresultfig\HDP_V.png')
plt.show()
print(cost)
# 绘制值函数V的轨迹
plt.figure(4)
plt.plot(cost, 'r')
plt.title('Train_loss_Trajecteory')
plt.xlabel('iter')
plt.ylabel('Train_loss')
plt.grid()
plt.savefig(r'ADPresultfig\HDP_loss.png')
plt.show()
# 绘制模型网络loss的轨迹
plt.figure(5)
plt.plot(modelloss, 'r')
plt.title('Model_loss_Trajecteory')
plt.xlabel('iter')
plt.ylabel('Model_loss')
plt.grid()
plt.savefig(r'ADPresultfig\HDP_Model_loss.png')
plt.show()
pass
########################################################################################################################
# 函数起始运行
# 在仿真时候,直接调用最优的模型进行仿真
# 最优的模型根据损失函数进行判断
########################################################################################################################
if __name__ == '__main__':
Agent = HDP() # 值迭代类实例化
Agent.learning() # 学习
Agent.simulator() # 仿真
代码说明
# 在计算最优输入的时候,直接通过采样来计算,而没有通过原始式子求导计算
# 在更新Actor Network时出现一个问题,已在作者另一篇博客中说明
代码运行说明
需要安装Pytorch
由于保存结果,因此需要在根目录先创建ADPresultfig文件夹
python文件只需要放在根目录下即可
结果
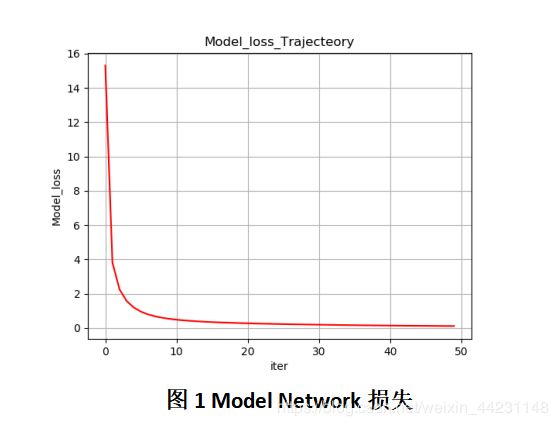
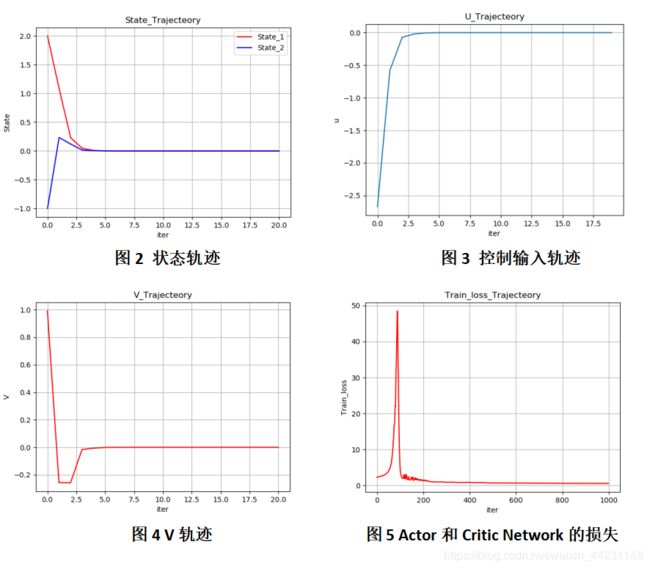
从图1看出,Model Network的损失逐渐趋近于0,说明Model Network能够以一定精度逼近系统。
图2显示了测试阶段系统两个状态的轨迹,可以看出经过3步,系统已经收敛到稳定点。图3表明输入也收敛为0V。图4表明V(Critic)也收敛为0。图5显示了在训练阶段Actor Network和Critic Network的损失值,起初有一定增长,但是随后逐渐收敛为0。
The End
文中的一些原理和图摘自其他出处,若有侵权,请告知,立马删除本文。
作者也是第一次写这方面代码,有理解错误的和代码错误的地方可以一起交流学习。
!!请勿转载本文!!
觉得作者写的还行就赏个脸,打赏一毛钱呗!哈哈哈