python求语音信号短时能量、短时过零率、语谱图
python语音信号处理(二)
一、短时能量
短时能量主要用于区分浊音段和清音段,因为浊音时E(i)值比清音时大得多;区分声母与韵母的分界和无话段与有话段分界。
计算第i帧语音信号yi(n)的短时能量公式为:
E ( i ) = ∑ n = 0 L − 1 y i 2 ( n ) , 1 < = i < = f n E(i)=\sum_{n=0}^{L-1}y_i^2(n),\qquad1<=i<=fn E(i)=n=0∑L−1yi2(n),1<=i<=fn
求一帧语音的短时能量,直接上代码:
import numpy as np
import wave
import matplotlib.pyplot as plt
wlen=512
inc=128
f = wave.open(r"lantian.wav", "rb")
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
str_data = f.readframes(nframes)
#print(str_data[:10])
wave_data = np.fromstring(str_data, dtype=np.short)
#print(wave_data[:10])
wave_data = wave_data*1.0/(max(abs(wave_data)))
print(wave_data[:10])
time = np.arange(0, wlen) * (1.0 / framerate)
signal_length=len(wave_data) #信号总长度
if signal_length<=wlen: #若信号长度小于一个帧的长度,则帧数定义为1
nf=1
else: #否则,计算帧的总长度
nf=int(np.ceil((1.0*signal_length-wlen+inc)/inc))
pad_length=int((nf-1)*inc+wlen) #所有帧加起来总的铺平后的长度
zeros=np.zeros((pad_length-signal_length,)) #不够的长度使用0填补,类似于FFT中的扩充数组操作
pad_signal=np.concatenate((wave_data,zeros)) #填补后的信号记为pad_signal
indices=np.tile(np.arange(0,wlen),(nf,1))+np.tile(np.arange(0,nf*inc,inc),(wlen,1)).T #相当于对所有帧的时间点进行抽取,得到nf*nw长度的矩阵
print(indices[:2])
indices=np.array(indices,dtype=np.int32) #将indices转化为矩阵
frames=pad_signal[indices] #得到帧信号
a=frames[30:31]
print(a[0])
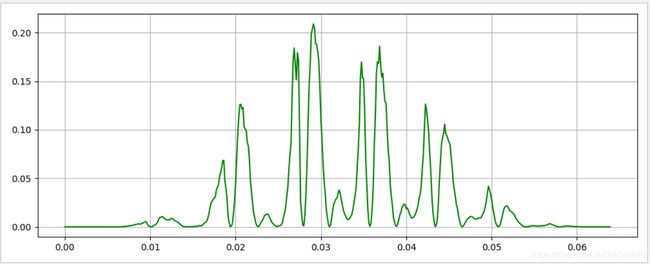
windown=np.hanning(512)
b=a[0]*windown
c=np.square(b)
plt.figure(figsize=(10,4))
plt.plot(time,c,c="g")
plt.grid()
plt.show()
信号加的是汉宁窗,上图为一帧语音的短时能量,下面为整段语音信号的短时能量。
import numpy as np
import wave
import matplotlib.pyplot as plt
wlen=512
inc=128
f = wave.open(r"lantian.wav", "rb")
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
str_data = f.readframes(nframes)
wave_data = np.fromstring(str_data, dtype=np.short)
wave_data = wave_data*1.0/(max(abs(wave_data)))
print(wave_data[:10])
signal_length=len(wave_data) #信号总长度
if signal_length<=wlen: #若信号长度小于一个帧的长度,则帧数定义为1
nf=1
else: #否则,计算帧的总长度
nf=int(np.ceil((1.0*signal_length-wlen+inc)/inc))
print(nf)
pad_length=int((nf-1)*inc+wlen) #所有帧加起来总的铺平后的长度
zeros=np.zeros((pad_length-signal_length,)) #不够的长度使用0填补,类似于FFT中的扩充数组操作
pad_signal=np.concatenate((wave_data,zeros)) #填补后的信号记为pad_signal
indices=np.tile(np.arange(0,wlen),(nf,1))+np.tile(np.arange(0,nf*inc,inc),(wlen,1)).T #相当于对所有帧的时间点进行抽取,得到nf*nw长度的矩阵
print(indices[:2])
indices=np.array(indices,dtype=np.int32) #将indices转化为矩阵
frames=pad_signal[indices] #得到帧信号
windown=np.hanning(wlen)
d=np.zeros(nf)
x=np.zeros(nf)
time = np.arange(0,nf) * (inc*1.0/framerate)
for i in range(0,nf):
a=frames[i:i+1]
b = a[0] * windown
c=np.square(b)
d[i]=np.sum(c)
d = d*1.0/(max(abs(d)))
print(d)
plt.figure(figsize=(10,4))
plt.plot(time,d,c="g")
plt.grid()
plt.show()
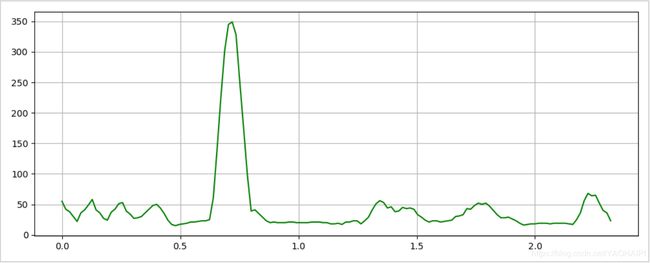
输出结果为:
该语音信号为普通话的“蓝天,白云”,可以比较清晰的看出短时能量的四个部分。
清音和浊音的区别:发清音时声带不振动,发浊音时声带振动。
二、短时平均过零率
短时平均过零率表示一帧语音中语音信号波形穿过横轴(零电平)的次数。过零率分析是.语音时域分析中最简单的一种。对于连续语音信号,过零即意味着时域波形通过时间轴;而对于离散信号,如果相邻的取样值改变符号,则称为过零。短时平均过零率就是样本数值改变符号的次数。
定义语音信号x(n)分帧后有yi(n),帧长为L,短时平均过零率为
Z ( i ) = 1 2 ∑ n = 0 L − 1 ∣ s g n [ y i ( n ) ] − s g n [ y i ( n − 1 ) ] ∣ , 1 < = i < = f n Z(i)=\frac{1}{2}\sum_{n=0}^{L-1}|sgn[y_{i}(n)]-sgn[y_i(n-1)]|,\qquad1<=i<=fn Z(i)=21n=0∑L−1∣sgn[yi(n)]−sgn[yi(n−1)]∣,1<=i<=fn
s g n [ n ] = { − 1 , x > = 0 1 , u < 0 sgn[n]=\begin{cases} -1,x>=0\\ 1, u<0\end{cases} sgn[n]={−1,x>=01,u<0
在实际计算短时平均过零率参数时,需要十分注意的一个问题是,如果输人信号中包含漂移,即信号在通往AD转换器前就有一个直流分量,使AD转换后继续带有这个直流分量。因为直流分量的存在影响了短时平均过零率的正确估算,所以建议在语音信号处理前先消除直流分量。
上代码:
import numpy as np
import wave
wlen=512
inc=128
import matplotlib.pyplot as plt
f = wave.open(r"lantian.wav", "rb")
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
str_data = f.readframes(nframes)
wave_data = np.fromstring(str_data, dtype=np.short)
wave_data = wave_data*1.0/(max(abs(wave_data)))
signal_length=len(wave_data) #信号总长度
if signal_length<=wlen: #若信号长度小于一个帧的长度,则帧数定义为1
nf=1
else: #否则,计算帧的总长度
nf=int(np.ceil((1.0*signal_length-wlen+inc)/inc))
pad_length=int((nf-1)*inc+wlen) #所有帧加起来总的铺平后的长度
zeros=np.zeros((pad_length-signal_length,)) #不够的长度使用0填补,类似于FFT中的扩充数组操作
pad_signal=np.concatenate((wave_data,zeros)) #填补后的信号记为pad_signal
indices=np.tile(np.arange(0,wlen),(nf,1))+np.tile(np.arange(0,nf*inc,inc),(wlen,1)).T #相当于对所有帧的时间点进行抽取,得到nf*nw长度的矩阵
print(indices[:2])
indices=np.array(indices,dtype=np.int32) #将indices转化为矩阵
frames=pad_signal[indices]
windown=np.hanning(wlen)
c=np.zeros(nf)
for i in range(nf):
a=frames[i:i+1]
b=windown*a[0]
for j in range(wlen-1):
if b[j]*b[j+1]<0:
c[i]=c[i]+1
time = np.arange(0,nf) * (inc*1.0/framerate)
plt.figure(figsize=(10,4))
plt.plot(time,c,c="g")
plt.grid()
plt.show()
输出结果:
通过分析语音信号发现,发浊音时,尽管声道有若干共振峰,但由于声门波引起谱的高频跌落,所以其语音能量约集中在3 kHz以下;而发清音时,多数能量出现在较高频率上。因为高频意味着高的短时平均过零率,低频意味着低的平均过零率,所以可以认为,浊音时具有较低的过零率,而清音时具有较高的过零率。当然,这种高低仅是相对而言的,并没有精确的数值关系。
利用短时平均过零率还可以从背景噪声中找出语音信号,可用于判断寂静无话段与有话段的起点和终点位置。在背景噪声较小时,用平均能量识别较为有效;而在背景噪声较大时,用短时平均过零率识别较为有效。
我们主要应用短时平均过零率来判断清音和浊音,有话段和无话段。
三、语音信号频域处理
在语音信号处理中,信号在频域或其他变换上的分析和处理占有重要地位,在频域和其他变换域上研究语音信号,可以使信号在时域上无法表现出来的某些特征变得十分明显。
下面将“蓝天,白云”这段语音信号转化为频域
import numpy as np
import wave
import matplotlib.pyplot as plt
f = wave.open(r"lantian.wav", "rb")
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
str_data = f.readframes(nframes)
wave_data = np.fromstring(str_data, dtype=np.short)
wave_data = wave_data*1.0/(max(abs(wave_data)))
fft_signal = np.fft.fft(wave_data) #语音信号FFT变换
fft_signal = abs(fft_signal)#取变换结果的模
plt.figure(figsize=(10,4))
time=np.arange(0,nframes)*framerate/nframes
plt.plot(time,fft_signal,c="g")
plt.grid()
plt.show()
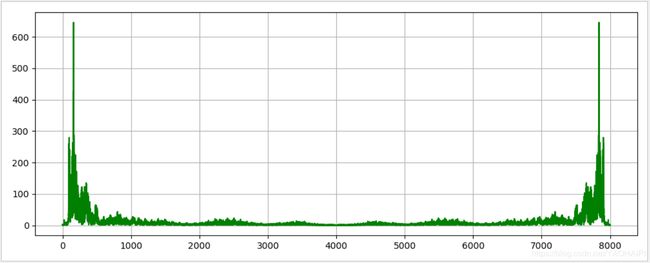
输出结果:
短时傅里叶变换
在信号处理发展史上,每一次理论上的突破都带来了信号处理领域的重大变革。传统傅里叶变换( Fourier Transform,FT)是以应用数学为基础建立起来的一门学科,它将信号分解为各个不同频率分量的组合,使信号的时域特征与频域特征联系起来,成为信号处理的有力工具。但是傅里叶变换使用的是一种全局变换,因此它无法表述信号的时频局域性质。为了能够分析处理非平稳信号,人们对傅里叶变换进行了推广,提出了短时傅里叶变换(Short Time Fou-rier Transform, STFT)和其他变换域上的处理,这些理论都可应用于语音信号分析处理。
短时傅里叶分析(Short Time Fourier Analysis, STFA)适用于分析缓慢时变信号的频谱分析,在语音分析处理中已经得到广泛应用。其方法是先将语音信号分帧,再将各帧进行傅里叶变换。每一帧语音信号可以被认为是从各个不同的平稳信号波形中截取出来的,各帧语音的短时频谱就是各个平稳信号波形频谱的近似。
由于语音信号是短时平稳的,因此可以·对·语音·进行·分帧处理,计算某一帧的傅里叶变换,这样得到的就是短时傅里叶变换,其定义为
X n ( e j w ) = ∑ m = − ∞ ∞ x ( m ) w ( n − m ) e j w X_n(e^{jw})=\sum_{m=-\infty}^{\infty}x(m)w(n-m)e^{jw} Xn(ejw)=m=−∞∑∞x(m)w(n−m)ejw
式中,下x(n)为语音信号序列:w(n)为实数窗序列,短时傅里叶变换是时间n和角频率w的函数,他反应了语音信号的频率随时间变化的特性。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RbV9gnE9-1573277367864)(C:\Users\jh\AppData\Roaming\Typora\typora-user-images\1572942290950.png)]
短时傅里叶变换有两种不同的解释,一种是当n固定不变时,X(ejw)为序列w(n-m)x(m)的标准傅里叶变换,此时X(ejw)具有与标准傅里叶变换相同的性质。另一种是当w固定不变时,可以将X(ejw)视为信号x(n)与窗函数指数加权w(n)ejw的卷积。
下面取语音的第50帧的语音信号做FFT变换:
import numpy as np
import wave
import matplotlib.pyplot as plt
wlen=512
inc=128
f = wave.open(r"lantian.wav", "rb")
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
str_data = f.readframes(nframes)
wave_data = np.fromstring(str_data, dtype=np.short)
wave_data = wave_data*1.0/(max(abs(wave_data)))
print(wave_data[:10])
signal_length=len(wave_data) #信号总长度
if signal_length<=wlen: #若信号长度小于一个帧的长度,则帧数定义为1
nf=1
else: #否则,计算帧的总长度
nf=int(np.ceil((1.0*signal_length-wlen+inc)/inc))
print(nf)
pad_length=int((nf-1)*inc+wlen) #所有帧加起来总的铺平后的长度
zeros=np.zeros((pad_length-signal_length,)) #不够的长度使用0填补,类似于FFT中的扩充数组操作
pad_signal=np.concatenate((wave_data,zeros)) #填补后的信号记为pad_signal
indices=np.tile(np.arange(0,wlen),(nf,1))+np.tile(np.arange(0,nf*inc,inc),(wlen,1)).T #相当于对所有帧的时间点进行抽取,得到nf*nw长度的矩阵
print(indices[:2])
indices=np.array(indices,dtype=np.int32) #将indices转化为矩阵
frames=pad_signal[indices] #得到帧信号
windown=np.hanning(wlen)
a=frames[50:51]
b=a[0]*windown
fft_signal = np.fft.fft(b)
fft_signal=abs(fft_signal)
time=np.arange(0,wlen)*framerate/nframes
plt.figure(figsize=(10,4))
plt.plot(time,fft_signal,c="g")
plt.grid()
plt.show()
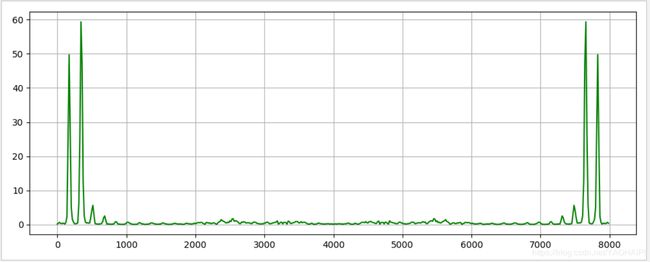
输出结果:
语普图
通过语音的短时傅里叶分析可以研究语音的短时频谱随时间的变化关系。在数字信号处理(Digital Signal Processing ,DSP)技术发展起来以前,人们就已经利用语谱仪来分析和记录语音信号的短时频谱。语谱仪是把语音的电信号送人一-组频率依次相接的窄带滤波器中,各个窄带滤波器的输出经整流均方后按频率由低到高的顺序记录在一卷记录纸上。信号的强弱由记录在纸上的灰度来表示:如果某个滤波器输出的信号强,相应的记录将浓黑;反之,则浅淡一些。记录纸按照一定的速度旋转,相当于按不同的时间记录了相应的滤波器输出。由此得到的图形就是语音信号的语谱图,其水平方向是时间轴,垂直方向是频率轴,图上的灰度条纹代表各个时刻的语音短时谱。语谱图反映了语音信号的动态频谱特性,在语音分析中具有重要的实用价值,被称为可视语音。
import numpy as np
import wave
import matplotlib.pyplot as plt
f = wave.open(r"lantian.wav", "rb")
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
str_data = f.readframes(nframes)
wave_data = np.fromstring(str_data, dtype=np.short)
wave_data = wave_data*1.0/(max(abs(wave_data)))
plt.specgram(wave_data,Fs = framerate, scale_by_freq = True, sides = 'default')
plt.show()
specgram()官网描述是:
matplotlib.pyplot.specgram(x, NFFT=None, Fs=None, Fc=None, detrend=None, window=None, noverlap=None, cmap=None, xextent=None, pad_to=None, sides=None, scale_by_freq=None, mode=None, scale=None, vmin=None, vmax=None, *, data=None, **kwargs)
参数:
x : 1-D array or sequence 数组或序列
Array or sequence containing the data.
数组或序列包含的数据。
Fs : scalar 标量
The sampling frequency (samples per time unit). It is used to calculate the Fourier frequencies, freqs, in cycles per time unit. The default value is 2.
抽样频率(每秒抽样数),用来计算傅里叶频率,以周期/时间单位表示。默认值为2
window : callable or ndarray 可调用的或无期限的
A function or a vector of length NFFT. To create window vectors see window_hanning, window_none, numpy.blackman, numpy.hamming, numpy.bartlett, scipy.signal, scipy.signal.get_window, etc. The default is window_hanning. If a function is passed as the argument, it must take a data segment as an argument and return the windowed version of the segment.
长度为nfft的函数或向量。要创建窗口向量,请参见window_hanning、window_none、numpy.blackman、numpy.hamming、numpy.bartlett、scipy.signal、scipy.signal.get_window等。默认值为window_hanning。如果函数作为参数传递,则必须将数据段作为参数,并返回该段的窗口版本。
sides : {‘default’, ‘onesided’, ‘twosided’}
Specifies which sides of the spectrum to return. Default gives the default behavior, which returns one-sided for real data and both for complex data. ‘onesided’ forces the return of a one-sided spectrum, while ‘twosided’ forces two-sided.
指定要返回频谱的哪一侧。默认值提供默认行为,对于实际数据和复杂数据都返回单面。单侧的力是单侧谱的返回,而“双侧的”力是双侧谱的返回。
pad_to : int
The number of points to which the data segment is padded when performing the FFT. This can be different from NFFT, which specifies the number of data points used. While not increasing the actual resolution of the spectrum (the minimum distance between resolvable peaks), this can give more points in the plot, allowing for more detail. This corresponds to the n parameter in the call to fft(). The default is None, which sets pad_to equal to NFFT
执行FFT时填充数据段的点数。这可能不同于NFFT,它指定使用的数据点数量。虽然不能增加频谱的实际分辨率(可分辨峰之间的最小距离),但这可以在图中给出更多的点,从而提供更多的细节。这对应于对fft()的调用中的n参数。默认值为无,它将pad_设置为等于nfft
NFFT : int
The number of data points used in each block for the FFT. A power 2 is most efficient. The default value is 256. This should NOT be used to get zero padding, or the scaling of the result will be incorrect. Use pad_to for this instead.
执行FFT时填充数据段的点数。这可能不同于NFFT,它指定使用的数据点数量。虽然不能增加光谱的实际分辨率(可分辨峰之间的最小距离),但这可以在图中给出更多的点,从而提供更多的细节。这对应于对fft()的调用中的n参数。默认值为无,它将pad_设置为等于nfft
detrend : {‘none’, ‘mean’, ‘linear’} or callable, default ‘none’
The function applied to each segment before fft-ing, designed to remove the mean or linear trend. Unlike in MATLAB, where the detrend parameter is a vector, in Matplotlib is it a function. The mlab module defines detrend_none, detrend_mean, and detrend_linear, but you can use a custom function as well. You can also use a string to choose one of the functions: ‘none’ calls detrend_none. ‘mean’ calls detrend_mean. ‘linear’ calls detrend_linear.
在FFT之前应用到每个段的函数,其被设计为去除平均值或线性趋势。与Matlab不同的是,dTrend参数是矢量,matplottlib是函数。MLAB模块定义DETrend_None、DeTrend_mean和DeTrend_Linear,但也可以使用自定义函数。您还可以使用字符串来选择其中一个函数:“无”调用deTrend_none。“mean”调用dTrend_mean。“线性”调用dTrend_linear。
scale_by_freq : bool, optional
Specifies whether the resulting density values should be scaled by the scaling frequency, which gives density in units of Hz^-1. This allows for integration over the returned frequency values. The default is True for MATLAB compatibility.
指定所产生的密度值是否应通过缩放频率进行缩放,该频率提供以Hz^-1为单位的密度。这允许对返回的频率值进行集成。默认情况下,MATLAB兼容性是正确的
mode : {‘default’, ‘psd’, ‘magnitude’, ‘angle’, ‘phase’}
What sort of spectrum to use. Default is ‘psd’, which takes the power spectral density. ‘magnitude’ returns the magnitude spectrum. ‘angle’ returns the phase spectrum without unwrapping. ‘phase’ returns the phase spectrum with unwrapping.
使用什么样的频谱。默认值是“psd”,它采用功率谱密度。Magnition“返回幅度谱。”Angle“返回相位谱而不展开。”“phase”返回展开后的相位谱。
noverlap : int
The number of points of overlap between blocks. The default value is 128.
块之间重叠点的数目。默认值是128。
scale : {‘default’, ‘linear’, ‘dB’}
The scaling of the values in the spec. ‘linear’ is no scaling. ‘dB’ returns the values in dB scale. When mode is ‘psd’, this is dB power (10 * log10). Otherwise this is dB amplitude (20 * log10). ‘default’ is ‘dB’ if mode is ‘psd’ or ‘magnitude’ and ‘linear’ otherwise. This must be ‘linear’ if mode is ‘angle’ or ‘phase’.
规范中值的缩放。“线性”不是缩放。‘db’返回db比例尺中的值。当模式为‘PSD’时,这是db功率(10log 10)。否则,这是db振幅(20log 10)。默认的是‘db’,如果模式是‘PSD’或‘大小’,‘线性’,否则。这必须是‘线性’,如果模式是‘角度’或‘相位’。
Fc : int
The center frequency of x (defaults to 0), which offsets the x extents of the plot to reflect the frequency range used when a signal is acquired and then filtered and downsampled to baseband.
x的中心频率(默认值为0),它抵消了图中的x个范围,以反映在获取信号、然后滤波和降采样到基带时所使用的频率范围。
cmap
A matplotlib.colors.Colormap instance; if None, use default determined by rc
matplotlib.chros.colmap实例;如果没有,则使用rc确定的默认值。
xextent : None or (xmin, xmax)
The image extent along the x-axis. The default sets xmin to the left border of the first bin (spectrum column) and xmax to the right border of the last bin. Note that for noverlap>0 the width of the bins is smaller than those of the segments.
沿x轴的图像范围。默认值为第一个bin(频谱列)的左边界和最后一个bin的右边界的xmax。请注意,对于NoVerlap>0,bin的宽度小于段的宽度。
**kwargs
Additional kwargs are passed on to imshow which makes the specgram image.
更多的kwargs被传递到图像中,这就产生了散斑图像。
返回值:
spectrum : 2-D array
Columns are the periodograms of successive segments.
列是连续段的周期图
freqs : 1-D array
The frequencies corresponding to the rows in spectrum.
与光谱中的行相对应的频率。
t : 1-D array
The times corresponding to midpoints of segments (i.e., the columns in spectrum).
对应于分段中点(即频谱中的列)的时间。
im : instance of class AxesImage
The image created by imshow containing the spectrogram
包含频谱图的图像
Notes
The parameters detrend and scale_by_freq do only apply when mode is set to ‘psd’.
只有当“模式”设置为“PSD”时,参数“按频率递减和缩放”才适用。
Note
In addition to the above described arguments, this function can take a data keyword argument. If such a data argument is given, the following arguments are replaced by data[]:
All arguments with the following names: ‘x’.
Objects passed as data must support item access (data[]) and membership test ( in data).
返回:
spectrum:频谱矩阵
freqs:频谱图每行对应的频率
ts:频谱图每列对应的时间
fig :图像
输出结果:
语谱图的横坐标是时间,纵坐标是频率,坐标点值为语音数据能量。由于是采用二维平面表达三维信息,所以能量值的大小是通过颜色来表示的,颜色深,表示该点的语音能量越强。
我们可以观察语音不同频段的信号强度随时间的变化情况。由于音乐信号本身频率丰富,不太容易看出规律,我们可以观察一下纯粹的语音数据的语谱图。从图中可以看到明显的一条条横方向的条纹,我们称为“声纹”,有很多应用。条纹的地方实际是颜色深的点聚集的地方,随时间延续,就延长成条纹,也就是表示语音中频率值为该点横坐标值的能量较强,在整个语音中所占比重大,那么相应影响人感知的效果要强烈得多。而一般语音中数据是周期性的,所以,能量强点的频率分布是频率周期的,即存在300Hz强点,则一般在n*300Hz点也会出现强点,所以我们看到的语谱图都是条纹状的。尽管客观人发声器官的音域是有限度的,即一般人发声最高频率为4000Hz,乐器的音域要比人宽很多,打击乐器的上限可以到20KHz。但是,由于我们数字分析频率时,采用的是算法实现的,一般是FFT,所以其结果是由采样率决定的,即尽管是上限为4000Hz的语音数据,如果采用16Khz的采样率来分析,则仍然可以在4000Hz以上的频段发现有数据分布,则可以认为是算法误差,非客观事实
语谱图生成流程(引用)
引用blog:
语音信号处理之(四)梅尔频率倒谱系数(MFCC)
我们处理的是语音信号,那么如何去描述它很重要。因为不同的描述方式放映它不同的信息。那怎样的描述方式才利于我们观测,利于我们理解呢?这里我们先来了解一个叫声谱图的东西。
![]()
这里,这段语音被分为很多帧,每帧语音都对应于一个频谱(通过短时FFT计算),频谱表示频率与能量的关系。在实际使用中,频谱图有三种,即线性振幅谱、对数振幅谱、自功率谱(对数振幅谱中各谱线的振幅都作了对数计算,所以其纵坐标的单位是dB(分贝)。这个变换的目的是使那些振幅较低的成分相对高振幅成分得以拉高,以便观察掩盖在低幅噪声中的周期信号)。
![]()
我们先将其中一帧语音的频谱通过坐标表示出来,如上图左。现在我们将左边的频谱旋转90度。得到中间的图。然后把这些幅度映射到一个灰度级表示(也可以理解为将连续的幅度量化为256个量化值?),0表示黑,255表示白色。幅度值越大,相应的区域越黑。这样就得到了最右边的图。那为什么要这样呢?为的是增加时间这个维度,这样就可以显示一段语音而不是一帧语音的频谱,而且可以直观的看到静态和动态的信息。优点稍后呈上。
这样我们会得到一个随着时间变化的频谱图,这个就是描述语音信号的spectrogram声谱图。
![]()
下图是一段语音的声谱图,很黑的地方就是频谱图中的峰值(共振峰formants)。
![]()
那我们为什么要在声谱图中表示语音呢?
首先,音素(Phones)的属性可以更好的在这里面观察出来。另外,通过观察共振峰和它们的转变可以更好的识别声音。隐马尔科夫模型(Hidden Markov Models)就是隐含地对声谱图进行建模以达到好的识别性能。还有一个作用就是它可以直观的评估TTS系统(text to speech)的好坏,直接对比合成的语音和自然的语音声谱图的匹配度即可。
研究加不同长度的窗函数对语谱图的影响
语谱图的时间分辨率和频率分辨率是由窗函数的特性决定的,可以按照短时傅里叶变换的第一种解释来分析频率分辨率。如果需要观察语音谐波的细节,则需要提高语谱图的频率分辨率,也就是减小窗函数的带通宽度。由于带通宽度是与窗函数成反比的,因此提高频率分辨率必须要增加窗长。这种情况下得到的语谱图称为窄带语谱图。
实际上就是信号的时宽越大(小),信号的频带宽度越小(大)
窄带语谱图
依然是上面的“蓝天,白云”的语音,语音采样频率为8000HZ,取窗长为512个数据点,帧移为窗长的1/4,即128个数据点。
import numpy as np
import wave
import matplotlib.pyplot as plt
def windows(name='Hamming', N=20):
# Rect/Hanning/Hamming
if name == 'Hamming':
window = np.array([0.54 - 0.46 * np.cos(2 * np.pi * n / (N - 1)) for n in range(N)])
elif name == 'Hanning':
window = np.array([0.5 - 0.5 * np.cos(2 * np.pi * n / (N - 1)) for n in range(N)])
elif name == 'Rect':
window = np.ones(N)
return window
f = wave.open(r"lantian.wav", "rb")
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
str_data = f.readframes(nframes)
wave_data = np.fromstring(str_data, dtype=np.short)
wave_data = wave_data*1.0/(max(abs(wave_data)))
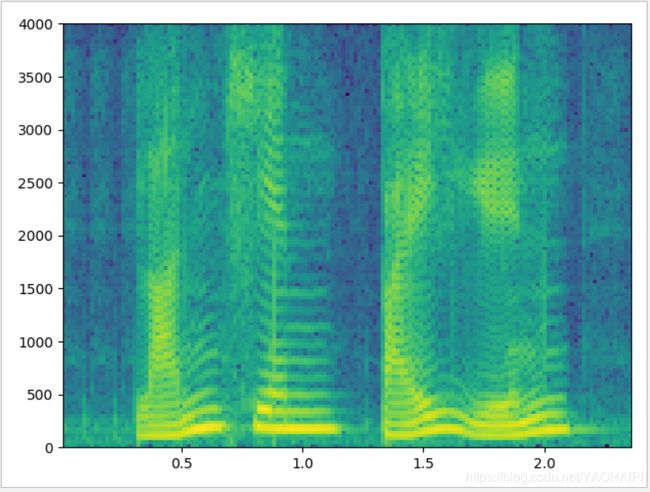
plt.specgram(wave_data,Fs = framerate,NFFT=512,window=windows("Hanning",512),noverlap=384,scale_by_freq = True, sides = 'default')
plt.show()
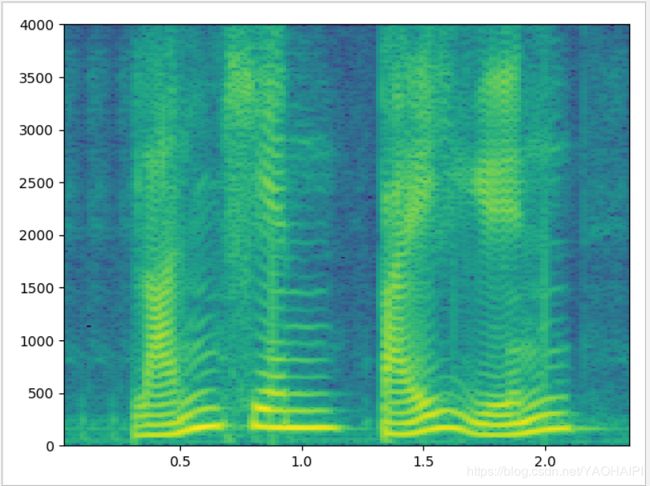
从结果图中可以清楚看到谐波的结构,频率分辨率非常好,但是时间上的分辨率就不理想.
窄带语谱图,频率分辨率太过精细,不能很好体现出共振峰的大致位置,即反映不出基波的变化特性。
宽带语谱图
依然是上面的“蓝天,白云”的语音,语音采样频率为8000HZ,取窗长为128个数据点,帧移为窗长的1/4,即32个数据点.
import numpy as np
import wave
import matplotlib.pyplot as plt
def windows(name='Hamming', N=20):
# Rect/Hanning/Hamming
if name == 'Hamming':
window = np.array([0.54 - 0.46 * np.cos(2 * np.pi * n / (N - 1)) for n in range(N)])
elif name == 'Hanning':
window = np.array([0.5 - 0.5 * np.cos(2 * np.pi * n / (N - 1)) for n in range(N)])
elif name == 'Rect':
window = np.ones(N)
return window
f = wave.open(r"lantian.wav", "rb")
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
str_data = f.readframes(nframes)
wave_data = np.fromstring(str_data, dtype=np.short)
wave_data = wave_data*1.0/(max(abs(wave_data)))
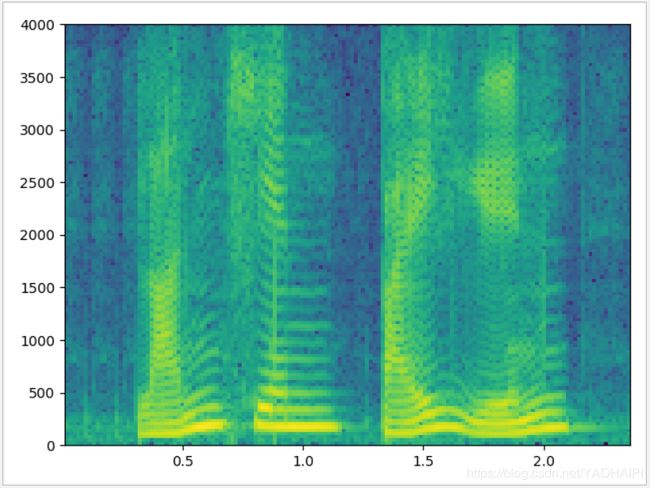
plt.specgram(wave_data,Fs = framerate,NFFT=128,window=windows("Hanning",128),noverlap=96,scale_by_freq = True, sides = 'default')
plt.show()
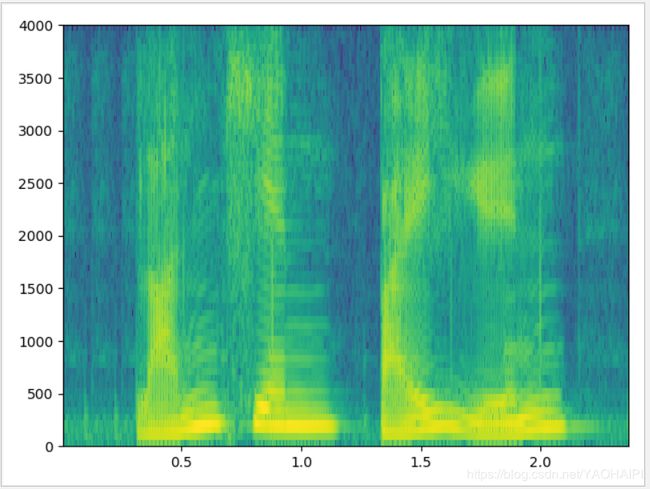
与窄带语谱图相反,宽带语谱图的时间分辨率很好,频率分辨率较低,不能很好反映声音的纹理特性,反映了频谱的时变特性,能很好分辨出共振峰的大致位置,但分辨不清谐波结构。
研究加不同窗对语谱图的影响
import numpy as np
import wave
import matplotlib.pyplot as plt
def windows(name='Hamming', N=20):
# Rect/Hanning/Hamming
if name == 'Hamming':
window = np.array([0.54 - 0.46 * np.cos(2 * np.pi * n / (N - 1)) for n in range(N)])
elif name == 'Hanning':
window = np.array([0.5 - 0.5 * np.cos(2 * np.pi * n / (N - 1)) for n in range(N)])
elif name == 'Rect':
window = np.ones(N)
return window
f = wave.open(r"lantian.wav", "rb")
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
str_data = f.readframes(nframes)
wave_data = np.fromstring(str_data, dtype=np.short)
wave_data = wave_data*1.0/(max(abs(wave_data)))
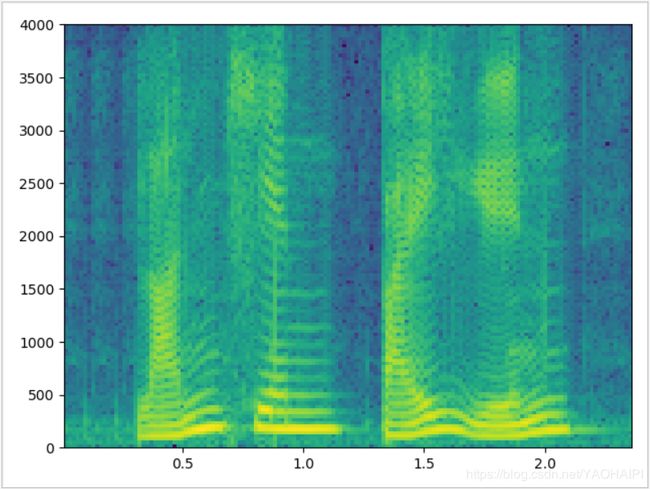
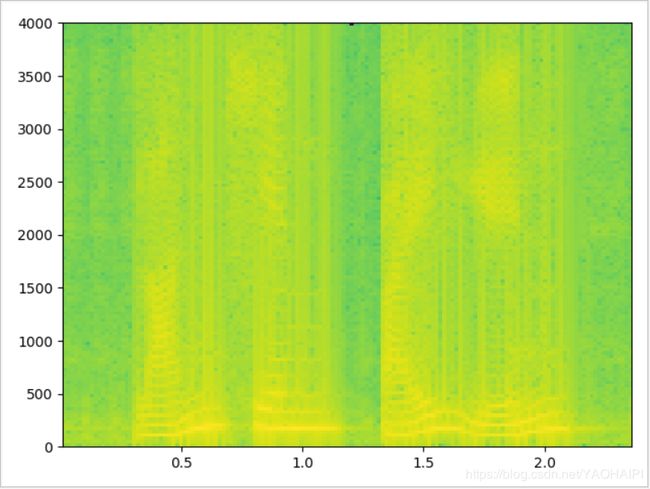
plt.specgram(wave_data,Fs = framerate, window=windows("Hanning",256),scale_by_freq = True, sides = 'default')
plt.show()
加汉明窗的效果图:
加矩形窗的效果图: