最小二乘拟合

最小二乘拟合

​ 假设有一组实验数据(xi，yi)，我们事先知道它们之间应该满足某函数关系： yi = f(xi)。通 过这些已知信息，需要确定函数 f()的一些参数。例如，如果函数 f()是线性函数f(x) = kx + b ，那么参数k和b 就是需要确定的值。
​ 如果用p 表示函数中需要确定的参数，则目标是找到一组P使得函数S 的值最小：

这种算法被称为最小二乘拟合(least-square fitting)。在 optimize模块中，可以使用leastsq()对数据进行最小二乘拟合计算。leastsq()的用法很简单，只需要将计箅误差的函数和待确定参数的 初始值传递给它即可。下面是用leastsq()对线性函数进行拟合的程序：

from scipy import optimize
import numpy as np
import  matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.family']='FangSong'
matplotlib.rcParams['font.size']=15
plt.rcParams['axes.unicode_minus']=False # 解决负号乱码问题

# 最小二乘拟合 
x = np.array([8.19,2.27,6.39,8.71,4.7,2.66,3.78])
y = np.array([7.01,2.78,6.47,6.71,4.1,4.23,4.05])

def residuals(p):
    "计算以p为参数的直线与原始数据之间的误差"
    k,b = p
    return y-(k*x+b)

# leastsq 使得residuals()的输出数组的平方和最小，参数的初始值[1,0]
r = optimize.leastsq(residuals,[1,0])
k,b = r[0]
print("k=%s,b=%s"%(k,b))

X=np.linspace(-10,10,100)
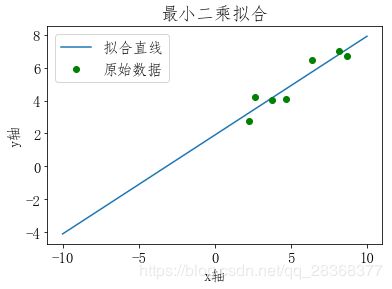
plt.plot(X,k*X+b,label=u"拟合直线")
plt.plot(x,y,"og",label=u"原始数据")
plt.legend()
plt.ylabel("y")
plt.xlabel("x")
plt.title(u"最小二乘拟合")

 

​ 直观地显示了拟合直线以及它们之间的误差。Oresiduals()的参数p 是拟合直线的参数，函数返回的是原始数据和拟合直线之间的误差。其中，数据点到拟合线距离表示误差。leastsq()使得这些误差的平方和最小。

例子：正弦波数据拟合

def func(x,p):
    """
    数据拟合所用的函数：A*sin(2*pi*k*x+theta)
    """
    A,k,theta = p
    return A*np.sin(2*np.pi*k*x+theta)

def residuals(p,y,x):
    """
    实验数据x,y和拟合函数之间的差,p为拟合所需要找到的系数
    """
    return y-func(x,p)

x = np.linspace(0,2*np.pi,100)
A ,k,theta = 10,0.34,np.pi/6 # 真实数据的函数参数
y0 = func(x,[A,k,theta]) # 真是数据

# 加入噪声之后的实验数据
np.random.seed(0)
y1 = y0 + 2*np.random.randn(len(x))
#print(2*np.random.randn(len(x)))
p0 = [7,0.4,0] # 第一次猜测的函数拟合参数

# 调用leastsq进行数据拟合
# residuals为计算误差函数
# p0为拟合参数的初始值
# args 为需要拟合的实验数据

plsq = optimize.leastsq(residuals,p0,args=(y1,x))

print("真实参数；%s"%[A,k,theta])
print("拟合参数:%s"%plsq[0])

plt.figure(figsize=(10,8),dpi=80)
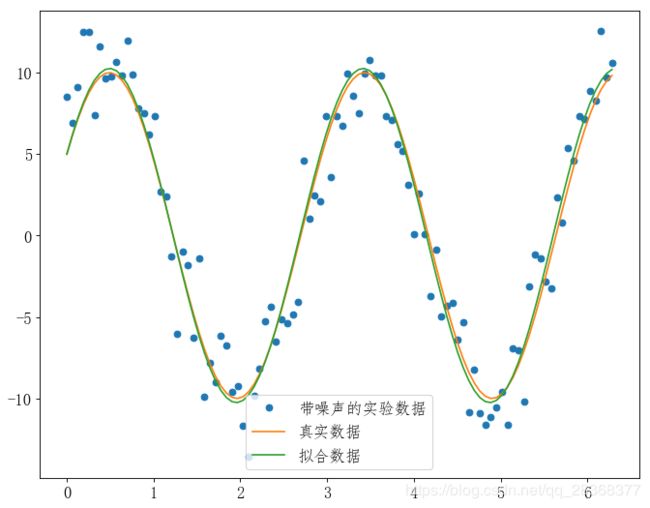
plt.plot(x,y1,"o",label="带噪声的实验数据")
plt.plot(x,y0,label="真实数据")
plt.plot(x,func(x,plsq[0]),label="拟合数据")
plt.legend()

真实参数；[10, 0.34, 0.5235987755982988]
拟合参数:[10.25218748  0.3423992   0.50817423]

 

​ 程序中，要拟合的目标函数func()是一个正弦函数，它的参数p 是一个数组，包含决定正弦波的三个参数A 、k 、theta, 分別对应正弦函数的振幅、频率和相角。待拟合的实验数据 是一组包含噪声的数据(x,y1) , 其中数组y1为标准正弦波数据y0加上随机噪声。
​ 用 leastsq()对带噪声的实验数据(x,y1)进行数据拟合，它可以找到数组x 和 y0之间的正弦关系，即确定A 、k 、theta等参数。和前而的直线拟合程序不同的是，这里我们将(y1，x )传递给 args参数。leastsq()会将这两个额外的参数传递给residuals()。 因此residuals()有三个参数，p 是 正弦函数的参数，y 和 x 是表示实验数据的数组。
​ 对于这利用 一维曲线拟合，optimize库还提供了一个curve_fit()函数，下而使用此函数对正弦波数据进行拟合。它的目标函数与leastsq()稍有不同，各个待优化参数直接作为函数的参数传入。

def func2(x,A,k,theta):
    return A*np.sin(2*np.pi*k*x+theta)

x = np.linspace(0,2*np.pi,100)
A,k,theta = 10,0.34,np.pi/6 # 真实数据的函数参数
y0 = func2(x,A,k,theta) # 真实数据
y1 = y0 + 2*np.random.randn(len(x)) # 加入噪声之后的实验数据
p0 = [7,0.4,0] # 第一次猜测的函数拟合参数
popt,_ = optimize.curve_fit(func2,x,y1,p0=p0)
print(popt)

[10.17528457  0.33765547  0.55404791]

​ 如果频率的初值和真实值的差别较大，拟合结果中的频率参数可能无法收敛于实际的频率。 在下面的例子中，由于频率初值的选择不当，导致curve_fit()未能收敛到真实的参数。这时可以通过其他方法先估算一个频率的近似值，或者使用全局优化算法。在后面的例子中，我们会使用全局优化算法重新对正弦波数据进行拟合。

def func2(x,A,k,theta):
    return A*np.sin(2*np.pi*k*x+theta)

x = np.linspace(0,2*np.pi,100)
A,k,theta = 10,0.34,np.pi/6 # 真实数据的函数参数
y0 = func2(x,A,k,theta) # 真实数据
y1 = y0 + 2*np.random.randn(len(x)) # 加入噪声之后的实验数据

popt,_ = optimize.curve_fit(func2,x,y1,p0=[10,1,0])
print("真实参数%s"%[A,k,theta])
print("拟合参数%s"%popt)

真实参数[10, 0.34, 0.5235987755982988]
拟合参数[ 1.30116633  1.04310843 -0.081064  ]

摘自《python科学计算》