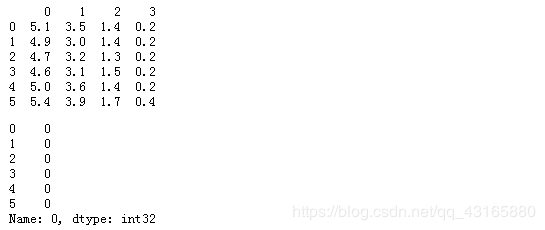python--支持向量机应用小例

以下内容笔记出自‘跟着迪哥学python数据分析与机器学习实战’，外加个人整理添加，仅供个人复习使用。

---

• SVM的分类效果
• 软间隔的作用，复杂算法容易造成过拟合，如何解决？
• 核函数的作用，核函数的作用，可以实现非线性分类。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import warnings
warnings.filterwarnings('ignore')
import os
#os.chdir(r'')
import matplotlib
%matplotlib inline
plt.rcParams['axes.labelsize']=14
plt.rcParams['xtick.labelsize']=12
plt.rcParams['ytick.labelsize']=12
plt.rcParams['font.sans-serif']='SimHei'

支持向量机基本建模

from sklearn.svm import SVC
from sklearn import datasets

iris=datasets.load_iris()  #字典形式数据
print(pd.DataFrame(iris['data']).head(6))
pd.DataFrame(iris['target']).iloc[:,0].head(6)

将自变量与因变量选择出来，建立简单模型：

#选择两列自变量 因变量两个类别
X=iris['data'][:,(2,3)]
y=iris['target']

setosa_or_versicolor=(y==0)|(y==1)
X=X[setosa_or_versicolor]
y=y[setosa_or_versicolor]

svm_clf=SVC(kernel='linear',C=float('inf'))
#线性分类问题，C无穷，表示精确分类，无软间隔问题
svm_clf.fit(X,y)

SVC(C=inf, break_ties=False, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=‘ovr’, degree=3, gamma=‘scale’, kernel=‘linear’,
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)

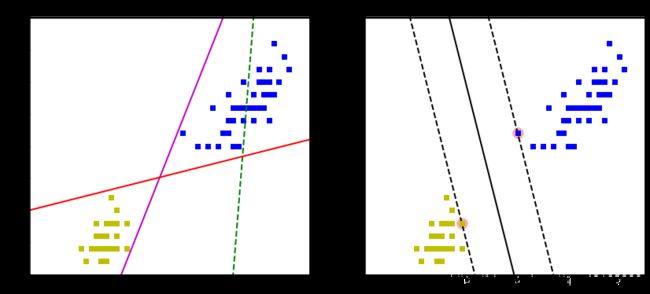
图形比较一般线性模型分类效果与支持向量机分类效果

#一般的线性模型
x0=np.linspace(0,5.5,200)
pred_1=5*x0-20
pred_2=x0-1.8
pred_3=0.1*x0+0.5

#定义svm作图图形（直接摘过来的）
def plot_svc_decision_boundary(svm_clf, xmin, xmax,sv=True):
    w = svm_clf.coef_[0]
    b = svm_clf.intercept_[0]
    print (w)    #snm决策方程参数
    x0 = np.linspace(xmin, xmax, 200)  #自变量
    decision_boundary = - w[0]/w[1] * x0 - b/w[1]    #svm决策方程
    
    margin = 1/w[1]
    gutter_up = decision_boundary + margin
    gutter_down = decision_boundary - margin   #添加间隔带
    
    if sv:
        svs = svm_clf.support_vectors_
        plt.scatter(svs[:,0],svs[:,1],s=180,facecolors='#FFAAAA')
    plt.plot(x0,decision_boundary,'k-',linewidth=2)
    plt.plot(x0,gutter_up,'k--',linewidth=2)
    plt.plot(x0,gutter_down,'k--',linewidth=2)

#做线性模型的图形
plt.figure(figsize=(14,6))
plt.subplot(121)
plt.plot(X[:,0][y==1],X[:,1][y==1],'bs')
plt.plot(X[:,0][y==0],X[:,1][y==0],'ys')  #两类散点
plt.plot(x0,pred_1,'g--',linewidth=2)
plt.plot(x0,pred_2,'m-',linewidth=2)
plt.plot(x0,pred_3,'r-',linewidth=2)
plt.axis([0,5.5,0,2])
plt.title('一般线性模型')

#做svm模型
plt.subplot(122)
plot_svc_decision_boundary(svm_clf, 0, 5.5)
plt.plot(X[:,0][y==1],X[:,1][y==1],'bs')
plt.plot(X[:,0][y==0],X[:,1][y==0],'ys')
plt.axis([0,5.5,0,2])
plt.title('支持向量机模型')

svm决策边界参数： [1.29411744 0.82352928]

加入软间隔

import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
'''
把多个处理数据的节点按顺序打包
最后一个节点需要实现fit()方法
其他节点需要实现fit()和transform()方法
'''
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC

iris=datasets.load_iris()
X=iris['data'][:,(2,3)] #petal length,petal width
y=(iris['target']==2).astype(np.float64)  #Iris-Viginice
#因变量y的选择是 种类是2的为1，种类是0和1的为0

#线性判断
svm_clf=Pipeline((
    ('std',StandardScaler()),
    ('linear_svc',LinearSVC(C=1))
))

svm_clf.fit(X,y)

svm_clf.predict([[5.5,1.7]])

array([1.])

对比不同C值的效果差异

C值影响了软间隔因子的大小，若C值大，那么软间隔小，表明分类较为严格，容易过拟合，若C值小，此时软间隔可以大些，这时分类的要求降低。

这里是用的最简单模型，两个自变量，二分类，线性分类。

建模

scaler=StandardScaler()
svm_clf1=LinearSVC(C=1,random_state=42)
svm_clf2=LinearSVC(C=100,random_state=42)

#第一个模型
scaled_svm_clf1=Pipeline((
    ('std',scaler),
    ('linear_svc',svm_clf1)
))

#第二个模型
scaled_svm_clf2=Pipeline((
    ('std',scaler),
    ('linear_svc',svm_clf2)
))

print('第一个模型',scaled_svm_clf1.fit(X,y))
print('第二个模型',scaled_svm_clf2.fit(X,y))

导出线性方程并做图

'''
既然是线性分类，线性方程可以导出来
'''
#截距项
b1=svm_clf1.decision_function([-scaler.mean_]/scaler.scale_) #标准化
b2 = svm_clf2.decision_function([-scaler.mean_ / scaler.scale_])
#参数
w1 = svm_clf1.coef_[0] / scaler.scale_  #标准化
w2 = svm_clf2.coef_[0] / scaler.scale_

svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])

svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])

print('第一个模型截距：',svm_clf1.intercept_,'\n',
     '第一个模型参数：',svm_clf1.coef_,'\n')

print('第二个模型截距：',svm_clf2.intercept_,'\n',
     '第二个模型参数：',svm_clf2.coef_)

第一个模型截距： [[-7.91669666]]
第一个模型参数： [[0.86508935 2.24726149]]

第二个模型截距： [[-13.64475178]]
第二个模型参数： [[1.72273715 3.20298118]]

作图：

plt.figure(figsize=(14,6))
plt.subplot(121)
#自变量
plt.plot(X[:,0][y==1],X[:,1][y==1],'g^',label='Virginica')
plt.plot(X[:,0][y==0],X[:,1][y==0],'bs',label='Versicolor')
#决策边界
plot_svc_decision_boundary(svm_clf1,4,6,sv=False)

plt.xlabel('length',fontsize=14)
plt.ylabel('width',fontsize=14)
plt.title('$C={}$'.format(svm_clf1.C),fontsize=16)
plt.axis([4,6,0.8,2.8])


plt.subplot(122)
#自变量
plt.plot(X[:,0][y==1],X[:,1][y==1],'g^')
plt.plot(X[:,0][y==0],X[:,1][y==0],'bs')
#决策边界
plot_svc_decision_boundary(svm_clf2,4,6,sv=False)
plt.xlabel('length',fontsize=14)
plt.title('$C={}$'.format(svm_clf2.C),fontsize=16)
plt.axis([4,6,0.8,2.8])

svm决策边界参数： [0.86508935 2.24726149]
svm决策边界参数： [1.72273715 3.20298118]

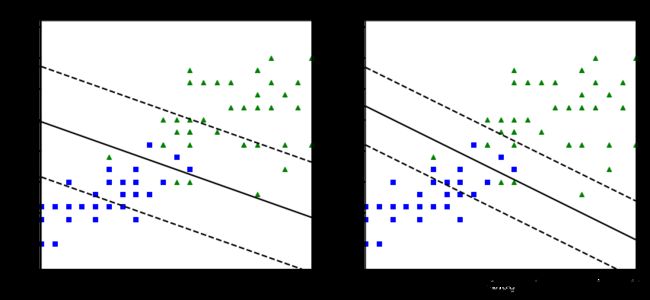
• 在右侧，使用较高的C值，分类器会减少误分类，但最终会有较小间隔
• 在左侧，使用较低的C值，间隔要大得多，但很多实例最终会出现在间隔之内。

非线性支持向量机

创建一份线性不可分的数据

from sklearn.datasets import make_moons
X,y=make_moons(n_samples=100,noise=0.15,random_state=42)

plt.rcParams['axes.unicode_minus']=False
def plot_dataset(X,y,axes):
    plt.plot(X[:,0][y==0],X[:,1][y==0],'bs')
    plt.plot(X[:,0][y==1],X[:,1][y==1],'g^')
    plt.axis(axes)
    plt.grid(True,which='both')
    plt.xlabel(r"$x_1$", fontsize=20)
    plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
    
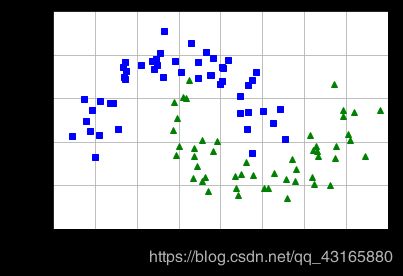
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.show()

利用多项式转换上述特征

多项式方法进行特征构造，a、b两个特征->(1,a,b,a2,ab,b2)

三个参数

• degree : 控制多项式的度
• interaction_only : 默认False，若为True，不会有a2和b2
• include_bias : 默认True，如果为True，会有1那一项

from sklearn.preprocessing import PolynomialFeatures

polynomial_svm_clf=Pipeline((
    ('poly_features',PolynomialFeatures(degree=3)),
    ('scaler',StandardScaler()),
    ('svm_clf',LinearSVC(C=10,loss='hinge'))
))
polynomial_svm_clf.fit(X,y)

#定义作图函数并作图
def plot_predictions(clf,axes):
    x0s=np.linspace(axes[0],axes[1],100)
    x1s=np.linspace(axes[2],axes[3],100)
    x0,x1=np.meshgrid(x0s,x1s)
    X=np.c_[x0.ravel(),x1.ravel()]
    y_pred=clf.predict(X).reshape(x0.shape)
    plt.contourf(x0,x1,y_pred,cmap=plt.cm.brg,alpha=0.2)
    
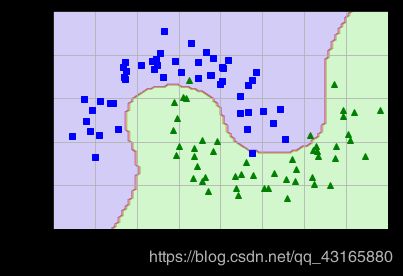
plot_predictions(polynomial_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])

使用核函数建模

多项式核函数

from sklearn.svm import SVC
#第一个模型
poly_kernel_svm_clf=Pipeline((
    ('scaler',StandardScaler()),
    ('svm_clf',SVC(kernel='poly',degree=3,   #多项式核函数
                  coef0=1,C=5))   #多项式为3，偏置项b=1,越小泛化性能越强？
))

poly_kernel_svm_clf.fit(X,y)

#第二个模型
poly100_kernel_svm_clf=Pipeline((
    ('scaler',StandardScaler()),
    ('svm_clf',SVC(kernel='poly',degree=10,
                  coef0=100,C=5))   #多项式为3，偏置项b=1,越小泛化性能越强？
))

poly100_kernel_svm_clf.fit(X,y)

作图：

plt.figure(figsize=(11,4))

plt.subplot(121)
plot_predictions(poly_kernel_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.title(r'$d=3,b=1,C=5',fontsize=18)

plt.subplot(122)
plot_predictions(poly100_kernel_svm_clf,[-1.5,2.5,-1,1.5])
plot_dataset(X,y,[-1.5,2.5,-1,1.5])
plt.title(r'$d=10,b=100,C=5',fontsize=18)

plt.show()

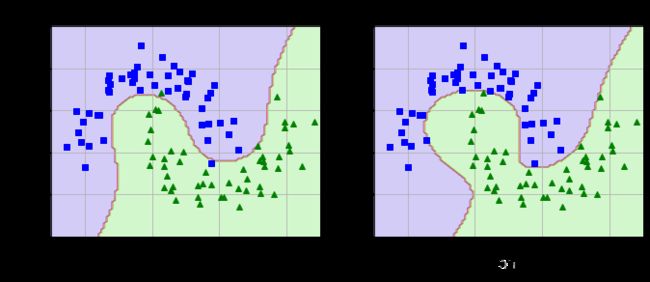
可以看到，degree越高，维度越高，越不易出现错误，模型越复杂，相应泛化能力越低。

而且这里用的是多项式核，一个图是degree=3，与上节先进行多项式特征转换的结果相同。

径向基核函数RBF

无论大样本还是小样本高维还是地位，RBF均适用。优点：

• RBF核函数可将一个样本映射到更高维空间，而且线性核函数是RBF的一个特例，也就是说如果考虑使用RBF，就没必要考虑线性核函数了。
• 与多项式核函数相比，RBF需要确定的参数要少，而核函数参数的多少直接影响函数的复杂程度。当多项式介绍比较高时，和矩阵的元素值将区域无穷大或无穷小，而RBF不会。
• 对于某些参数，RBF和sigmoid具有相似的性能

另外的参数gamma

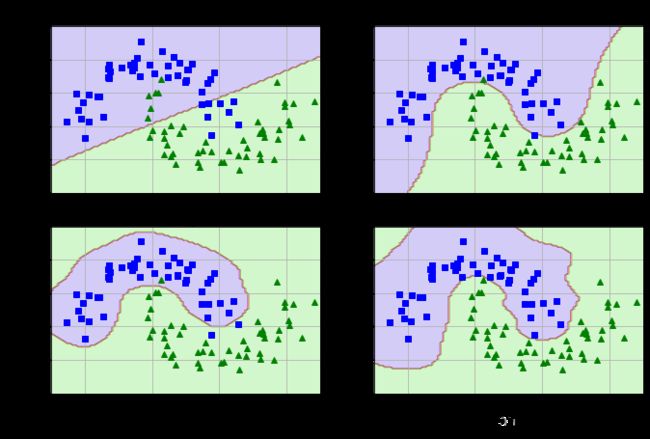
• 增加gamma : 增加复杂度，高斯曲线变窄，每个实例的影响范围都较小，决策边界变得不规则，在个别实例周围摆动。
• 减少gamma : 降低复杂度，高斯曲线变宽，实例具有更大影响范围，决策边界更平滑

rbf_kernel_svm_clf=Pipeline((
    ('scaler',StandardScaler()),
    ('svm_clf',SVC(kernel='rbf',gamma=5,C=0.001))
))

rbf_kernel_svm_clf.fit(X,y)

from sklearn.svm import SVC

gamma1,gamma2=0.1,5
C1,C2=0.001,1000
hyperparams=(gamma1,C1),(gamma1,C2),(gamma2,C1),(gamma2,C2)

svm_clfs=[]
for gamma,C in hyperparams:
    rbf_kernel_svm_clf=Pipeline([
        ('scaler',StandardScaler()),
        ('svm_clf',SVC(kernel='rbf',gamma=gamma,C=C))
    ])
    rbf_kernel_svm_clf.fit(X,y)
    svm_clfs.append(rbf_kernel_svm_clf)

plt.figure(figsize=(11,7))
for i,svm_clf in enumerate(svm_clfs):
    plt.subplot(221+i)
    plot_predictions(svm_clf,[-1.5,2.5,-1,1.5])
    plot_dataset(X,y,[-1.5,2.5,-1,1.5])
    gamma,C=hyperparams[i]
    plt.title(r'$\gamma={},C={}$'.format(gamma,C),fontsize=16)
plt.show()

可以看到，gamma越大，C越大，模型复杂度越高.