动态规划 —— 线性 DP —— 字符串编辑距离
【概述】
字符串编辑距离，即 Levenshtein 距离，是俄国科学家 Vladimir Levenshtein 提出的概念，是指从一个字符串修改到另一个字符串时，编辑单个字符所需的最少次数，编辑单个字符允许的操作有：替换、插入、删除。
Levenshtein 距离一般用来衡量两个字符串的相似度，一般来说，两个字符串的编辑距离越小，相似度越大。
举例来说，从 "set" 改到 "sitting" 需要 5 次单字符编辑操作：
- e 修改为 i：sit
- 添加 t：sitt
- 添加 i：sitti
- 添加 n：sittin
- 添加 g：sitting
因此，set 与 sitting 的编辑距离为：3
【Levenshtein 算法】
Levenshtein 算法又称编辑距离（Edit Distance）算法，用于求两个长度分别为 n、m的字符串 a、b 的 Levenshtein 距离，其是一个线性动态规划的算法，时空复杂度均为 O(nm)。
1. 状态转移方程
对于两个字符串 a、b，其长度为 |a|、|b|，他们间的编辑距离定义为：
其中，
是指字符串 a 的前 i 个字符和字符串 b 的前 j 个字符的编辑距离。
在有了编辑距离后，字符串 a、b 的相似度定义为：
2.算法原理
对于 a、b 两个字符串来说，我们先考虑极端的情况，即 a 或 b 的长度为 0 时，那么要编辑的次数就是另一个字符串的长度。
之后，我们考虑一般情况，在 k 个操作中有：
- 删除操作：将 a[1],a[2],...,a[i-1] 转换为 b[1],b[2],...,b[j]
- 插入操作：将 a[1],a[2],...,a[i] 转换为 b[1],b[2],...,b[j-1]
- 替换操作：将 a[1],a[2],...,a[i-1] 转换为 b[1],b[2],...,b[j-1]
对于删除操作，只需将 a[i] 从 a 中移除，即可完成转换，此时编辑次数为 k+1
对于插入操作，只需在 a[i] 后加上 b[j]，即可完成转换，此时编辑次数为 k+1
对于替换操作，只需将 a[i] 转换为 b[j]，即可完成转换，需要注意的是，如果 a[i] 与 b[j] 相同，那么此时编辑次数为 k，如果 a[i] 与 b[j] 不同，那么此时编辑次数为 k+1
而为了保证将 a[1],a[2],...,a[i] 转换为 b[1],b[2],...,b[j] 的操作次数是最少的，因此要在三种情况中取最小值，故而只需要按此逻辑进行迭代，保证每一步操作都是最小即可。
3.实例
我们以字符串 a：abroad 与字符串 b：aboard 为例，并在计算过程中将每一步的操作数放入 i+1 行 j+1 列的二维数组 dp 中，此时 dp[i][j] 即为将 a[1],a[2],...,a[i] 转换为 b[1],b[2],...,b[j] 所需的最小操作数。
首先考虑极端情况，即 a 为空字符串或 b 为空字符串时，需要的操作此时为另一字符串的长度，即：dp[i][0]=i，dp[0][j]=j
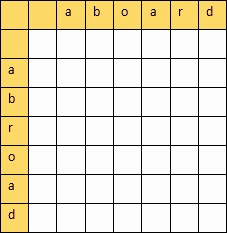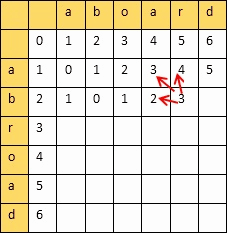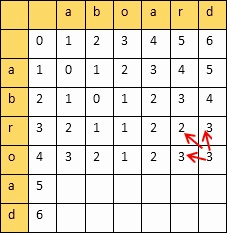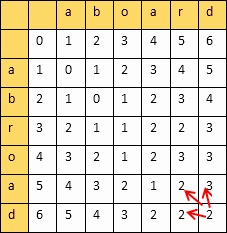
之后我们考虑一般情况，从头到尾遍历这个二维数组，从第一行到最后一行，根据定义来计算 dp[i][j] 的值，即 dp[i][j] 的值由 dp[i][j] 的上方元素 dp[i-1][j]、左方元素 dp[i][j-1]、左上方元素 dp[i-1][j-1] 的值来计算得出
最后 dp[aLen][bLen] 即为字符串 a 转换到 b 的 Levenshtein 距离。
如下图，最终 "abroad" 与 "aboard" 的 Levenshtein 距离 
，相似度 
4.实现
char a[N], b[N];
int dp[N][N];
int main() {
scanf("%s%s", a, b);
int aLen = strlen(a);
int bLen = strlen(b);
//极端情况
for (int i = 1; i <= aLen; i++) //以i+1来考虑第i个字符的情况
dp[i][0] = i;
for (int j = 1; j <= bLen; j++) //以j+1来考虑第j个字符的情况
dp[j][0] = j;
for (int i = 1; i <= aLen; i++) { //以i+1来考虑第i个字符的情况
for (int j = 1; j <= bLen; j++) { //以j+1来考虑第j个字符的情况
if (a[i - 1] == b[j - 1]) //相同时距离不变
dp[i][j] = dp[i - 1][j - 1];
else //不同时取三个位置的最小值再+1
dp[i][j] = min(dp[i - 1][j - 1],min(dp[i - 1][j], dp[i][j - 1])) + 1;
}
}
printf("%d\n", dp[aLen][bLen]);
return 0;
}