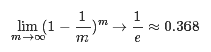集成学习-模型融合学习笔记(附Python代码)
1 集成学习概述
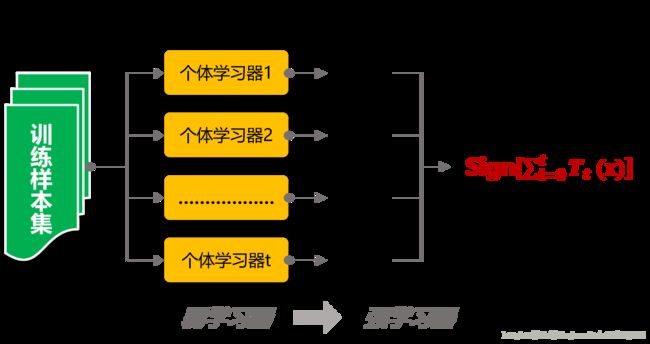
集成学习(Ensemble Learning)是一种能在各种的机器学习任务上提高准确率的强有力技术,其通过组合多个基分类器(base classifier)来完成学习任务。基分类器一般采用的是弱可学习(weakly learnable)分类器,通过集成学习,组合成一个强可学习(strongly learnable)分类器。所谓弱可学习,是指学习的正确率仅略优于随机猜测的多项式学习算法;强可学习指正确率较高的多项式学习算法。集成学习的泛化能力一般比单一的基分类器要好,这是因为大部分基分类器的分类错误的概率远低于单一基分类器的。可能这么说还不是很理解这个问题,下面将从投票集成的例子出发,逐步梳理集成学习的脉络。
图1 集成学习示意图
为什么集成模型能够减少错误率?为什么它能在模型间相关度较低时能取得更好的结果?针对以上问题,接下来逐步进行讲解。
纠错码
在航天任务中,所有的信号都被正确的传达是非常重要的。
如果我们有一个二进制字符串形式的信号,如:
1110110011101111011111011011如果信号在传输过程中有一位发生了翻转(第二位),变成了
1010110011101111011111011011在航天任务中这可能是致命的。针对这种情况,在纠错码中有一个编码解决方案。在最简单的情况下,即纠错码是重复码时:以同样大小的数据块多次传递信号,并进行投票(以少数服从多数原则)。
#原始信号:
1110110011
#10分块数据:
10,3 101011001111101100111110110011
#编码:
1010110011
1110110011
1110110011
#投票结果:
1110110011信号失真很少发生且通常在局部发生,因此,多次投票依然出错的可能性就更小了。只要信号失真不是完全不可预测的(有50%的几率发生),信号就能被修复。
举一个机器学习的例子
假设我们的测试集有10个样本,正确的情况应该都是1:
1111111111我们有3个正确率为70%的二分类器记为A、B、C。你可以将这些分类器视为伪随机数产生器,以70%的概率产生”1”,30%的概率产生”0”。
下面我们会展示这些伪分类器通过投票集成的方法得到78%的正确率。
涉及到一点数学知识
#三个全正确的概率
0.7 * 0.7 * 0.7
= 0.3429
#两个正确的概率
0.7 * 0.7 * 0.3
+ 0.7 * 0.3 * 0.7
+ 0.3 * 0.7 * 0.7
= 0.4409
#两个错误的概率
0.3 * 0.3 * 0.7
+ 0.3 * 0.7 * 0.3
+ 0.7 * 0.3 * 0.3
= 0.189
#三个全错误的概率
0.3 * 0.3 * 0.3
= 0.027可以看出有44%的概率投票可以校正大部分错误。大部分投票集成会使最终的准确率变成78%左右(0.3429 + 0.4409 = 0.7838)。
差异性
周志华教授在他的著作《机器学习》中提到,结果的差异性越高,最终模型融合出来的结果也会越好。同样用一个简单的例子来证明:接着上面的话题,假设现在三个模型预测出来的结果是
model1:1111111100 = 80% 准确率
model2:1111111100 = 80% 准确率
model3:1011111100 = 70% 准确率如果把这三个模型结果用多数表决组合起来,那么最终结果是:1111111100 = 80%,这个结果跟第一、二个模型是一致的,也就是,这样的模型融合对最终结果没有任何的提升。
假如我们现在把三个模型结果改为:
model1:1111111100 = 80% 准确率
model2:0111011101 = 70% 准确率
model3:1000101111 = 60% 准确率显然这三个模型之间的差异更大,而且表面来看性能也不如前面提到的三个模型,但它们融合出来的结果是:1111111101 = 90% 准确率!
以上,我们采用的是多数表决融合的方式,即每个投票者的权重都是一样的。此外,还有加权表决融合和结果平均两种方式。
加权表决融合
多数表决的融合方式默认了所有模型的重要度是一样的,但通常情况下我们会更重视表现较好的模型而需要赋予更大的权值。在加权表决的情况下,表现较差的模型只能通过与其他模型获得一样的结果来增强自己的说服力。
对结果取平均
对结果取平均在很多机器学习问题上以及不同的评估准则上都获得很不错的结果。
取均值的做法常常可以减少过拟合现象。在机器学习的应用上,过拟合现象是很普遍的,根本问题是训练数据量不足以支撑复杂的模型,导致模型学习到数据集上的噪音,这样产生的问题是模型很难泛化,因为模型“考虑”得过分片面。
但如果对结果取平均,可以在一定程度上减轻过拟合现象。图2中所示,单个模型因为过拟合产生了绿色的决策边界,但事实上黑色的决策边界因为有更好的泛化能力从而有更好的效果。如果通过拟合多个模型并对模型结果取平均,对这些噪音点的考虑就会因为结果拉平均的原因而减少,决策边界也会慢慢的往黑色线靠拢。
图2 决策边界
记住,机器学习的目的并不是让模型记住训练数据,而是对未知数据有更好的推广。
同时,我们也必须注意到,上面的分析有一个关键假设:基学习器的误差相互独立。在现实任务中,个体学习器是为解决同一个问题训练出来的,它们显然不可能相互独立!事实上,个体学习器的”准确性”和”多样性”本身就存在冲突。一般的,准确性很高之后,要增加多样性就需牺牲准确性。事实上,如何产生并结合”好而不同“的个体学习器,恰是集成学习研究的核心。
目前,集成学习中常用的方法有Bagging、Boosting、Blending、Stacking等,接下来将从原理和代码两方面对以上方法进行讲解。
2 集成学习方法
2.1 Bagging
Bagging是并行式集成学习方法最著名的代表。给定包含 m 个样本的数据集,我们先随机取出一个样本放入采样集中,再把该样本放回初始数据集,使得下次采样时该样本仍有可能被选中,经过 m 次随机采样操作,我们得到含 m 个样本的采样集,初始训练集中有的样本在采样集里多次出现,有的则从未出现。
Bagging的策略如下:
- 从样本集中重采样(有重复的)选出n个样本
- 在所有属性上,对这n个样本建立分类器(ID3、C4.5、CART、SVM、Logistic回归等)
- 重复1、2…… m 次,即获得了 m 个分类器
- 将数据放在这m个分类器上,最后根据这 m 个分类器的投票结果,决定数据属于哪一类
图3 Bagging示意图
2.1.1 OOB数据
Bagging采用的重采样,即为评估方法中的自助法(bootstrapping)。可以做一个简单的估计,样本在m次采样中始终不被采到的概率是
![]()
取极限得到:
即通过自主法采样,初始数据集中有约36.8%的样本未出现在采样数据集中,将这些未参与模型训练的数据称为袋外数据(包外估计,out-of-bag estimate)。
2.1.2 随机森林
随机森林(Random Forest,简称 RF)是 Bagging的一个扩展变体。其在以决策树为基学习器构建 Bagging 集成的基础上,进一步在决策树的训练过程中引入了随机属性选择。
随机森林的策略如下:
- 从样本集中用Bootstrap采样选出n个样本
- 从所有属性中随机选择k个属性,选择最佳分割属性作为节点建立CART决策树
- 重复1、2两个步骤,即建立了m棵CART决策树
- m个CART形成随机森林,通过投票表决结果,决定数据属于哪一类
k 控制了随机性的引入程度;若令 k = d , 则基决策树的构建与传统决策树相同;若令 k = 1 , 则是随机选择一个属性用于划分 ; 一般情况下,推荐值为
![]()
随机森林简单、容易实现、计算开销小,在很多现实任务中展现出强大的性能,被誉为”代表集成学习技术水平的方法”。可以看出,随机森林对 Bagging 只做了小改动 ,但是与 Bagging 中基学习器的”多样性”仅通过样本扰动(通过对初始训练集采样)而来不同,随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,这就使得最终集成的泛化性能可通过个体学习器之间差异度的增加而进一步提升。
2.1.3 代码实现
下面是决策树以及Bagging和随机森林在UCI的Breast cancer数据集上的表现。
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
#读入乳腺癌数据集
data=load_breast_cancer()
x=pd.DataFrame(data.data)
y=data.target
#划分数据集
X_train,X_test,y_train,y_test=train_test_split(x,y,random_state=0,test_size=0.3)
# 度量单个决策树的准确性
tree = DecisionTreeClassifier(criterion='entropy', max_depth=None)
tree = tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train, y_train_pred)
tree_test = accuracy_score(y_test, y_test_pred)
print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train, tree_test))
#Decision tree train/test accuracies 1.000/0.942
# 度量bagging分类器的准确性
# 生成500个决策树,详细的参数建议参考官方文档
bag = BaggingClassifier(base_estimator=tree, n_estimators=500, max_samples=1.0, max_features=1.0, bootstrap=True, bootstrap_features=False, n_jobs=1, random_state=1)
bag = bag.fit(X_train, y_train)
y_train_pred = bag.predict(X_train)
y_test_pred = bag.predict(X_test)
bag_train = accuracy_score(y_train, y_train_pred)
bag_test = accuracy_score(y_test, y_test_pred)
print('Bagging train/test accuracies %.3f/%.3f' % (bag_train, bag_test))
#Bagging train/test accuracies 1.000/0.959
#随机森林,bagging思想
rf = RandomForestClassifier(n_estimators=1000, max_features='sqrt', max_depth=None, min_samples_split=2, bootstrap=True, n_jobs=1, random_state=1)
# 度量随机森林的准确性
rf = rf.fit(X_train, y_train)
y_train_pred = rf.predict(X_train)
y_test_pred = rf.predict(X_test)
tree_train = accuracy_score(y_train, y_train_pred)
tree_test = accuracy_score(y_test, y_test_pred)
print('Random Forest train/test accuracies %.3f/%.3f' % (tree_train, tree_test))
#RandomFores train/test accuracies 1.000/0.971其输出结果是
Decision tree train/test accuracies 1.000/0.942
Bagging train/test accuracies 1.000/0.959
Random Forest train/test accuracies 1.000/0.9712.2 Boosting
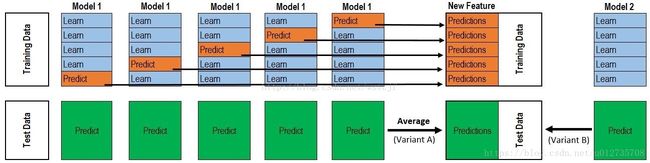
Boosting 是一族可将弱学习器提升为强学习器的算法。这族算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直至基学习器数目达到事先指定的值 T , 最终将这 T 个基学习器进行加权结合。Boosting 算法工作机制如下图所示:
图4 Boosting示意图
2.2.1 AdaBoost
Boosting在直接构造强学习器非常困难的情况下,为学习算法的设计提供了一种有效的新思路和新方法。其中最为成功应用的是,Yoav Freund和Robert Schapire在1995年提出的AdaBoost算法。
Adaboost算法可以简述为三个步骤:
- 初始化训练数据的权值分布D1。假设有N个训练样本数据,则每一个训练样本最开始时,都被赋予相同的权值:w1=1/N。
- 训练弱分类器hi。具体训练过程中是:如果某个训练样本点,被弱分类器hi准确地分类,那么在构造下一个训练集中,它对应的权值要减小;相反,如果某个训练样本点被错误分类,那么它的权值就应该增大。权值更新过的样本集被用于训练下一个分类器,整个训练过程如此迭代地进行下去。
- 将各个训练得到的弱分类器组合成一个强分类器。各个弱分类器的训练过程结束后,加大分类误差率小的弱分类器的权重,使其在最终的分类函数中起着较大的决定作用,而降低分类误差率大的弱分类器的权重,使其在最终的分类函数中起着较小的决定作用。
换而言之,误差率低的弱分类器在最终分类器中占的权重较大,否则较小。
2.2.2 GBDT
GBDT也是集成学习Boosting家族的成员,但是却和传统的Adaboost有很大的不同。在Adaboost中,我们是利用前一轮迭代弱学习器的误差率来更新训练集的权重,这样一轮轮的迭代下去。GBDT也是迭代,使用了前向分布算法,但是弱学习器限定了只能使用CART回归树模型,同时迭代思路和Adaboost也有所不同。
GBDT的思想可以用一个通俗的例子解释,假如有个人30岁,我们首先用20岁去拟合,发现损失有10岁,这时我们用6岁去拟合剩下的损失,发现差距还有4岁,第三轮我们用3岁拟合剩下的差距,差距就只有一岁了。如果我们的迭代轮数还没有完,可以继续迭代下面,每一轮迭代,拟合的岁数误差都会减小。
2.2.3 XGBoost
相对于传统的GBDT,XGBoost使用了二阶信息,可以更快的在训练集上收敛。这可是kaggle等各类比赛的大杀器!
由于“随机森林族”本身具备过拟合的优势,因此XGBoost仍然一定程度的具有该特性。
XGBoost的实现中使用了并行/多核计算,因此训练速度快;同时他的原生语言为C/C++,这是它速度快的原因。
2.2.4 代码实现
下面是决策树、AdaBoost、GBDT和XGBoost在UCI的Breast cancer数据集上的表现。
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import GradientBoostingClassifier
import xgboost
from sklearn.metrics import accuracy_score
#读入乳腺癌数据集
data=load_breast_cancer()
x=pd.DataFrame(data.data)
y=data.target
#划分数据集
X_train,X_test,y_train,y_test=train_test_split(x,y,random_state=0,test_size=0.3)
# 度量单个决策树的准确性
tree = DecisionTreeClassifier(criterion='entropy', max_depth=None)
tree = tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train, y_train_pred)
tree_test = accuracy_score(y_test, y_test_pred)
print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train, tree_test))
#Decision tree train/test accuracies 1.000/0.942
# Boosting分类器准确性
ada = AdaBoostClassifier(n_estimators=1000, learning_rate=0.1, random_state=0)
ada = ada.fit(X_train, y_train)
y_train_pred = ada.predict(X_train)
y_test_pred = ada.predict(X_test)
ada_train = accuracy_score(y_train, y_train_pred)
ada_test = accuracy_score(y_test, y_test_pred)
print('AdaBoost train/test accuracies %.3f/%.3f' % (ada_train, ada_test))
# AdaBoost train/test accuracies 1.000/0.977
gbdt =GradientBoostingClassifier(n_estimators=1000, learning_rate=0.1, random_state=0)
gbdt= gbdt.fit(X_train, y_train)
y_train_pred = gbdt.predict(X_train)
y_test_pred = gbdt.predict(X_test)
gbdt_train = accuracy_score(y_train, y_train_pred)
gbdt_test = accuracy_score(y_test, y_test_pred)
print('GBDT train/test accuracies %.3f/%.3f' % (gbdt_train, gbdt_test))
# GBDT train/test accuracies 1.000/0.982
xgb =xgboost.XGBClassifier(n_estimators=1000, learning_rate=0.1)
xgb= xgb.fit(X_train, y_train)
y_train_pred = xgb.predict(X_train)
y_test_pred = xgb.predict(X_test)
xgb_train = accuracy_score(y_train, y_train_pred)
xgb_test = accuracy_score(y_test, y_test_pred)
print('XGBoost train/test accuracies %.3f/%.3f' % (xgb_train, xgb_test))
# XGBoost train/test accuracies 1.000/0.982其输出结果是
Decision tree train/test accuracies 1.000/0.971
AdaBoost train/test accuracies 1.000/0.977
GBDT train/test accuracies 1.000/0.982
XGBoost train/test accuracies 1.000/0.9822.3 Stacking和Blending
Stacking和Blending是两种集成分类器的相似方法,在实际中应用Stacking较多,此处以Stacking进行讲解。
Stacking是一种分层模型集成框架。以两层为例,第一层由多个基学习器组成,其输入为原始训练集,第二层的模型则是以第一层基学习器的输出作为特征加入训练集进行再训练,从而得到完整的Stacking模型。
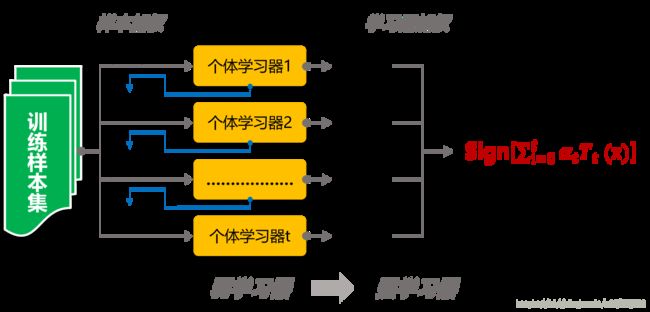
Stacking的过程有一张图非常经典,如下:
图5 Stacking过程
虽然他很直观,但是没有语言描述确实很难搞懂。看完我是很懵的,最后看了相关文章的详细描述才搞懂。这里我到一篇讲解比较好的文章,引用其文章内容将这个过程进行详细描述。
2.3.1 Stacking过程描述
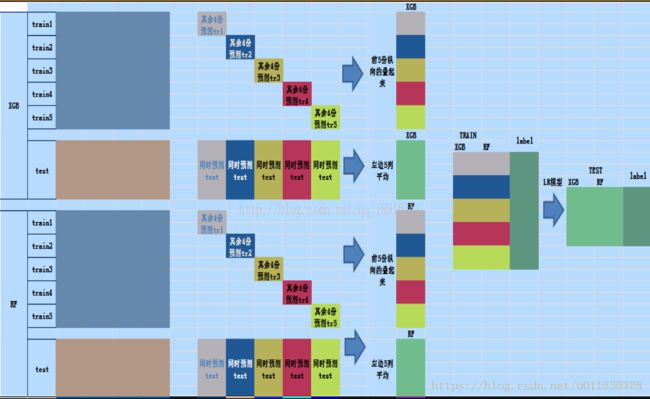
图5的上半部分是用一个基础模型进行5折交叉验证,如:用XGBoost作为基础模型Model1,5折交叉验证就是先拿出四折作为training data,另外一折作为testing data。注意:在stacking中此部分数据会用到整个traing set。如:假设我们整个training set包含10000行数据,testing set包含2500行数据,那么每一次交叉验证其实就是对training set进行划分,在每一次的交叉验证中training data将会是8000行,testing data是2000行。
每一次的交叉验证包含两个过程,1. 基于training data训练模型;2. 基于training data训练生成的模型对testing data进行预测。在整个第一次的交叉验证完成之后我们将会得到关于当前testing data的预测值,这将会是一个一维2000行的数据,记为a1。注意!在这部分操作完成后,我们还要对数据集原来的整个testing set进行预测,这个过程会生成2500个预测值,这部分预测值将会作为下一层模型testing data的一部分,记为b1。因为我们进行的是5折交叉验证,所以以上提及的过程将会进行五次,最终会生成针对testing set数据预测的5列2000行的数据a1、a2,、a3、a4、a5,对testing set的预测会是5列2500行数据b1、b2、b3、b4、b5。
在完成对Model1的整个步骤之后,我们可以发现a1、a2、a3、a4、a5其实就是对原来整个training set的预测值,将他们拼凑起来,会形成一个10000行一列的矩阵,记为A1。而对于b1、b2、b3、b4、b5这部分数据,我们将各部分相加取平均值,得到一个2500行一列的矩阵,记为B1。
以上就是stacking中一个模型的完整流程,stacking中同一层通常包含多个模型,假设还有Model2: LR,Model3:RF,Model4: GBDT,Model5:SVM,对于这四个模型,我们可以重复以上的步骤,在整个流程结束之后,我们可以得到新的A2、A3、A4、A5、B2、B3、B4、B5矩阵。
在此之后,我们把A1、A2、A3、A4、A5并列合并得到一个10000行五列的矩阵作为training data,B1、B2、B3、B4、B5并列合并得到一个2500行五列的矩阵作为testing data。让下一层的模型,基于他们进一步训练。
以上即为stacking的完整步骤!为了方便理解,这里借用了该文章的插图。
图6 Stacking详细过程
2.3.2 Blending与Stacking的区别
Blending与Stacking大致相同,只是Blending的主要区别在于训练集不是通过K-Fold的CV策略来获得预测值从而生成第二阶段模型的特征,而是建立一个Holdout集,例如说10%的训练数据,第二阶段的stacker模型就基于第一阶段模型对这10%训练数据的预测值进行拟合。说白了,就是把Stacking流程中的K-Fold CV 改成 HoldOut CV。
Blending的优点在于:
- 比stacking简单(因为不用进行k次的交叉验证来获得stacker feature)
- 避开了一个信息泄露问题:generlizers和stacker使用了不一样的数据集
- 在团队建模过程中,不需要给队友分享自己的随机种子
而缺点在于:
- 使用了很少的数据(第二阶段的blender只使用training set10%的量)
- blender可能会过拟合(其实大概率是第一点导致的)
- stacking使用多次的CV会比较稳健
对于实践中的结果而言,stacking和blending的效果是差不多的,所以使用哪种方法都没什么所谓,完全取决于个人爱好。
2.3.3 代码实现
from __future__ import division
import numpy as np
from sklearn.cross_validation import train_test_split
from sklearn.datasets import load_breast_cancer
from sklearn.cross_validation import StratifiedKFold
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
if __name__ == '__main__':
np.random.seed(0) # seed to shuffle the train set
n_folds = 10
verbose = True
shuffle = False
data=load_breast_cancer()
X=data.data
y=data.target
#划分数据集
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0,test_size=0.2)
if shuffle:
idx = np.random.permutation(y_train.size)
X_train = X_train[idx]
y_train = y_train[idx]
skf = list(StratifiedKFold(y_train, n_folds))
clfs = [RandomForestClassifier(n_estimators=100, n_jobs=-1, criterion='gini'),
RandomForestClassifier(n_estimators=100, n_jobs=-1, criterion='entropy'),
ExtraTreesClassifier(n_estimators=100, n_jobs=-1, criterion='gini'),
ExtraTreesClassifier(n_estimators=100, n_jobs=-1, criterion='entropy'),
GradientBoostingClassifier(learning_rate=0.05, subsample=0.5, max_depth=6, n_estimators=100)]
print( "Creating train and test sets for stacking.")
dataset_blend_train = np.zeros((X_train.shape[0], len(clfs)))
dataset_blend_test = np.zeros((X_test.shape[0], len(clfs)))
for j, clf in enumerate(clfs):
print (j, clf)
dataset_blend_test_j = np.zeros((X_test.shape[0], len(skf)))
for i, (train, test) in enumerate(skf):
print("Fold", i)
X_train_b = X_train[train]
y_train_b = y_train[train]
X_test_b = X_train[test]
y_test_b = y_train[test]
clf.fit(X_train_b, y_train_b)
y_submission = clf.predict_proba(X_test_b)[:, 1]
dataset_blend_train[test, j] = y_submission
dataset_blend_test_j[:, i] = clf.predict_proba(X_test)[:, 1]
dataset_blend_test[:, j] = dataset_blend_test_j.mean(1)
print( "Stacking.")
clf = LogisticRegression()
clf.fit(dataset_blend_train, y_train)
print("Stacking Accuracy %0.6f:"%accuracy_score(y_test,clf.predict(dataset_blend_test)))
n=1
for model in clfs:
model.fit(X_train,y_train)
y_test_pred = model.predict(X_test)
print("模型%d,Accuracy %0.6f:"%(n,accuracy_score(y_test,y_test_pred)))
n=n+1其输出结果是
Stacking Accuracy 0.973684:
模型1,Accuracy 0.956140:
模型2,Accuracy 0.964912:
模型3,Accuracy 0.973684:
模型4,Accuracy 0.956140:
模型5,Accuracy 0.973684:2.3.4 Heamy实现
针对Stacking和Blending,数据科学竞赛工具集heamy中已经打包实现,可以直接调用。通过pip install heamy进行安装。具体使用说明参考文档:https://heamy.readthedocs.io/en/latest/
Stacking
from heamy.dataset import Dataset
from heamy.estimator import Regressor, Classifier
from heamy.pipeline import ModelsPipeline
from sklearn import cross_validation
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
#加载数据集
from sklearn.datasets import load_boston
data = load_boston()
X, y = data['data'], data['target']
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.1, random_state=111)
#创建数据集
dataset = Dataset(X_train,y_train,X_test)
#创建RF模型和LR模型
model_rf = Regressor(dataset=dataset, estimator=RandomForestRegressor, parameters={'n_estimators': 50},name='rf')
model_lr = Regressor(dataset=dataset, estimator=LinearRegression, parameters={'normalize': True},name='lr')
# Stack两个模型
# Returns new dataset with out-of-fold predictions
pipeline = ModelsPipeline(model_rf,model_lr)
stack_ds = pipeline.stack(k=10,seed=111)
#第二层使用lr模型stack
stacker = Regressor(dataset=stack_ds, estimator=LinearRegression)
results = stacker.predict()
# 使用10折交叉验证结果
results10 = stacker.validate(k=10,scorer=mean_absolute_error)Blending
from heamy.dataset import Dataset
from heamy.estimator import Regressor, Classifier
from heamy.pipeline import ModelsPipeline
from sklearn import cross_validation
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
#加载数据集
from sklearn.datasets import load_boston
data = load_boston()
X, y = data['data'], data['target']
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.1, random_state=111)
#创建数据集
dataset = Dataset(X_train,y_train,X_test)
#创建RF模型和LR模型
model_rf = Regressor(dataset=dataset, estimator=RandomForestRegressor, parameters={'n_estimators': 50},name='rf')
model_lr = Regressor(dataset=dataset, estimator=LinearRegression, parameters={'normalize': True},name='lr')
# Blending两个模型
# Returns new dataset with out-of-fold predictions
pipeline = ModelsPipeline(model_rf,model_lr)
stack_ds = pipeline.blend(proportion=0.2,seed=111)
#第二层使用lr模型stack
stacker = Regressor(dataset=stack_ds, estimator=LinearRegression)
results = stacker.predict()
# 使用10折交叉验证结果
results10 = stacker.validate(k=10,scorer=mean_absolute_error)加权平均
from heamy.dataset import Dataset
from heamy.estimator import Regressor, Classifier
from heamy.pipeline import ModelsPipeline
from sklearn import cross_validation
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error
from sklearn.neighbors import KNeighborsRegressor
from sklearn.datasets import load_boston
data = load_boston()
X, y = data['data'], data['target']
X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.1, random_state=111)
#创建数据集
dataset = Dataset(X_train,y_train,X_test)
model_rf = Regressor(dataset=dataset, estimator=RandomForestRegressor, parameters={'n_estimators': 151},name='rf')
model_lr = Regressor(dataset=dataset, estimator=LinearRegression, parameters={'normalize': True},name='lr')
model_knn = Regressor(dataset=dataset, estimator=KNeighborsRegressor, parameters={'n_neighbors': 15},name='knn')
pipeline = ModelsPipeline(model_rf,model_lr,model_knn)
weights = pipeline.find_weights(mean_absolute_error)
result = pipeline.weight(weights)本文主要旨在梳理模型融合的方法,各方法的原理涉及的很少,想详细了解的请通过其他方式深入学习。
3 致谢
非常感谢前辈们的分享,部分参考资料如下:
https://blog.csdn.net/dkjkls/article/details/79955464
https://blog.csdn.net/ruiyiin/article/details/77114072
https://blog.csdn.net/a358463121/article/details/53054686
https://blog.csdn.net/u011630575/article/details/81302994
https://blog.csdn.net/sinat_29819401/article/details/71191219
https://github.com/emanuele/kaggle_pbr/blob/master/blend.py