剑指offer刷题（二）（21-43）题

21 栈的压入、弹出

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）

class Solution {
public:
    bool IsPopOrder(vector p1,vector p2) {
        
        if(p1.empty() || p2.empty() || p1.size()!= p2.size() )return false;
        stack s;
        int index = 0;
        
        for(int i = 0; i < p1.size(); i++){
            s.push(p1[i]);//先把p1数据压入栈
            
            //如果栈顶元素和p2元素相同则弹出栈顶元素 并使索引自增
            // p1 1 2 3 4 5     p2 4 5 3 2 1 
            // 当压入4时 此时 index = 0  p2[index] = 4 所以把4弹出栈 index自增到1
            // 5同理
            // 此时栈中的元素为 1 2 3 p2[2 - 4]元素为 3 2 1 刚好相反 能把栈中的所有元素弹出
            // 当循环结束 栈为空 说明是符合弹出序列的
            while(!s.empty() && s.top() == p2[index]){
                index++;
                s.pop();
            }
        }
        
        return s.empty();
    }
};

22 从上往下打印二叉树

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};
二叉树的层序遍历
用一个队列依次把每层每个结点装入队列
当队列不为空时循环执行出队
直到队列没有结点
*/
class Solution {
public:
    vector PrintFromTopToBottom(TreeNode* root) {
        vector res;
        if(!root) return res;
        queue q;
        q.push(root);//先把根结点入队
        while(q.size()){//当队列不为空时
            auto cur = q.front();//取出队首元素
            res.push_back(cur->val);//存储队首元素
            q.pop();//队首元素出队
            if(cur->left)q.push(cur->left);//如果当前结点有左孩子，左孩子入队
            if(cur->right)q.push(cur->right);//如果当前结点有右孩子，右孩子入队
        }
        return res;
    }
};

23 二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

/*
BST的后序序列的合法序列是，对于一个序列S，最后一个元素是x （也就是根），
如果去掉最后一个元素的序列为T，那么T满足：T可以分成两段，
前一段（左子树）小于x，后一段（右子树）大于x，
且这两段（子树）都是合法的后序序列。
*/

class Solution {
public:
    bool VerifySquenceOfBST(vector seq) {
        if(seq.size() == 0) return false;
        return dfs(seq, 0, seq.size() - 1);
    }
    bool dfs(vector &seq, int s, int e){
        if(s >= e)return true;
        // r 是 最后一个元素 第一步 可以看作root
        int r = seq[e], l = s;
        //取得左子树所有的数
        while(seq[l] < r) l++;
        // 如果右子树中 有比root小的 肯定不是BST 直接返回false
        for(int i = l; i < e; i++)if(r > seq[i])return false;
        
        //递归搜索root的左子树和右子树 要两个子树都满足 左子树 < root 和 右子树 > root
        return dfs(seq, s, l - 1) && dfs(seq, l, e - 1);
    }
};

24 二叉树中和为某一值的路径

输入一颗二叉树的跟节点和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中，数组长度大的数组靠前)

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};
这题就是dfs
取一个数组来记录路径
每次先向左子树找 假如当前左子树的结点的值小于余下的sum值
就用sum减去当前结点的值 然后继续往左子树递归 如果左子树不满足 就向右子树
当减去左子树或右子树的结点的值后 不满足 回溯 删除路径数组中的最后一个结点
*/
class Solution {
public:
    vector > FindPath(TreeNode* root,int expectNumber) {
        vector> res; 
        vector path;
        dfs(root, expectNumber, res, path);
        return res;
    }
    void dfs(TreeNode *root, int sum, vector> &res, vector &path) {

        if(!root) return;//如果当前结点为空 则退出递归
        path.push_back(root->val);//加入路径数组
        sum = sum - root->val;//和减去当前结点的值
        if(!root->left && !root->right && !sum) res.push_back(path);//sum为0并且左右子树都为空，就是找到一条path
        if(root->left)  dfs(root->left, sum, res, path);//向左子树递归
        if(root->right) dfs(root->right, sum, res, path);//向右子树递归
        path.pop_back();//回溯法  一定要恢复现场！

    }

};

25 复杂链表的复制

输入一个复杂链表（每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针指向任意一个节点），返回结果为复制后复杂链表的head。（注意，输出结果中请不要返回参数中的节点引用，否则判题程序会直接返回空）

（1）每个结点复制一个与其相同的结点接到其屁股后面

（2）每个复制结点的random指向原来结点指向的下一个结点，现在算是全部复制，但是有两个同样的
（3）所以第三步就是分离原来的结点和复制的结点，不用考虑random，只需把所有clone结点串起来

/*
struct RandomListNode {
    int label;
    struct RandomListNode *next, *random;
    RandomListNode(int x) :
            label(x), next(NULL), random(NULL) {
    }
};
这题有难度 不过也有规律
分三个步骤：
（1）每个结点复制一个与其相同的结点接到其屁股后面
（2）每个复制结点的random指向原来结点指向的下一个结点，现在算是全部复制，但是有两个同样的
（3）所以第三步就是分离原来的结点和复制的结点，不用考虑random，只需把所有clone结点串起来
*/
class Solution {
public:
    // 先不管random 每个结点复制和自己结点一样的放到自己后面
    RandomListNode *CloneNodes(RandomListNode *pHead)
    {
        auto node = pHead;
        while (node){
            auto tempNode = new RandomListNode(node->label);
            tempNode->next = node->next;
            node->next = tempNode;
            node = tempNode->next;
        }
        return pHead;
    }
    //  每个clone结点的random指向原先指向的后一个结点
    RandomListNode *ConnectRandomNodes(RandomListNode *pHead)
    {
        auto node = pHead;
        while (node){
            auto tempNode = node->next;
            if(node->random)tempNode->random = node->random->next;
            node = tempNode->next;
        }
        return pHead;
    }
    // 分离结点，cloneHead取pHead->next直到结束
    RandomListNode *ReConnectRandomNodes(RandomListNode *pHead)
    {
        auto node = pHead;
        RandomListNode *cloneHead = nullptr;
        RandomListNode *cloneNode = nullptr;
        if(node){
            cloneHead = cloneNode = node->next;
            node->next = cloneNode->next;
            node = node->next;
        }
        while (node){
            cloneNode->next = node->next;
            cloneNode = cloneNode->next;
            node->next = cloneNode->next;
            node = node->next;
        }
        return cloneHead;
    }
    RandomListNode* Clone(RandomListNode* pHead)
    {
        return ReConnectRandomNodes(ConnectRandomNodes(CloneNodes(pHead)));
    }
};

26 二叉搜索树与双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
/*利用平衡二叉树中序遍历有序的特点，例如：

           10
          /  \
         8   14

维护一个last变量，存储当前双向链表的最后一个节点。当中序遍历到10时，last应该指向8。

将10的left指针指向8，如果8不为NULL，将8的right指针指向10，然后last指向10。
*/
class Solution {
public:
    TreeNode* last = NULL;
    TreeNode* Convert(TreeNode* r)
    {
        dfs(r);
        
        auto head = last;
        while(head && head->left)head = head->left;
        return head;
    }
    void dfs(TreeNode* r){
        if(!r)return;
        auto cur = r;
        if(cur->left)Convert(cur->left);
        
        cur->left = last;
        if(last) last->right = cur;
        last = cur;
        
        if(cur->right)Convert(cur->right);
    }
};

27 字符串的排列

输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。

/*
经典的dfs 入门 不知道怎么说
在回溯时 要么把tmp最后一个字符弹出 要么把字符交换回来 
*/

class Solution {
public:
    vector Permutation(string str) {
        vector res;
        if(str.size() == 0)return res;
        string tmp;
        dfs(str, tmp, res, 0);
        return res;
    }
    void dfs(string str, string &tmp, vector &res, int start){
        if(start < 0 || str.size() == 0)return;
        if(str.size() == start){
            res.push_back(tmp);
            return;
        }
        for(int i = start; i < str.size(); i++){
            if( i != start && str[i] == str[start])continue;//如果字符相同，不用交换
            swap(str[i],str[start]);
            tmp += str[start];
            dfs(str,tmp,res,start + 1);
            tmp.pop_back();//回溯法的关键,恢复上一个现场
        }
    }
    
};

看不明白的 可以看这个高分答案，Java写的：

import java.util.ArrayList;
import java.util.List;
import java.util.Collections;
public class Solution {
    public ArrayList Permutation(String str) {
        List resultList = new ArrayList<>();
        if(str.length() == 0)
            return (ArrayList)resultList;
        //递归的初始值为（str数组，空的list，初始下标0）
        fun(str.toCharArray(),resultList,0);
        Collections.sort(resultList);
        return (ArrayList)resultList;
    }
     
    private void fun(char[] ch,List list,int i){
        //这是递归的终止条件，就是i下标已经移到char数组的末尾的时候，考虑添加这一组字符串进入结果集中
        if(i == ch.length-1){
            //判断一下是否重复
            if(!list.contains(new String(ch))){
                list.add(new String(ch));
                return;
            }
        }else{
            //这一段就是回溯法，这里以"abc"为例
             
            //递归的思想与栈的入栈和出栈是一样的,某一个状态遇到return结束了之后，会回到被调用的地方继续执行
             
            //1.第一次进到这里是ch=['a','b','c'],list=[],i=0，我称为 状态A ，即初始状态
            //那么j=0，swap(ch,0,0)，就是['a','b','c']，进入递归，自己调自己，只是i为1，交换(0,0)位置之后的状态我称为 状态B 
            //i不等于2，来到这里，j=1，执行第一个swap(ch,1,1)，这个状态我称为 状态C1 ,再进入fun函数，此时标记为T1，i为2，那么这时就进入上一个if，将"abc"放进list中
            /////////////-------》此时结果集为["abc"]
             
            //2.执行完list.add之后，遇到return，回退到T1处，接下来执行第二个swap(ch,1,1)，状态C1又恢复为状态B
            //恢复完之后，继续执行for循环，此时j=2,那么swap(ch,1,2),得到"acb"，这个状态我称为C2,然后执行fun，此时标记为T2,发现i+1=2,所以也被添加进结果集，此时return回退到T2处往下执行
            /////////////-------》此时结果集为["abc","acb"]
            //然后执行第二个swap(ch,1,2)，状态C2回归状态B,然后状态B的for循环退出回到状态A
             
            //             a|b|c(状态A)
            //               |
            //               |swap(0,0)
            //               |
            //             a|b|c(状态B)
            //             /  \
            //   swap(1,1)/    \swap(1,2)  (状态C1和状态C2)
            //           /      \
            //         a|b|c   a|c|b
             
            //3.回到状态A之后，继续for循环，j=1,即swap(ch,0,1)，即"bac",这个状态可以再次叫做状态A,下面的步骤同上
            /////////////-------》此时结果集为["abc","acb","bac","bca"]
             
            //             a|b|c(状态A)
            //               |
            //               |swap(0,1)
            //               |
            //             b|a|c(状态B)
            //             /  \
            //   swap(1,1)/    \swap(1,2)  (状态C1和状态C2)
            //           /      \
            //         b|a|c   b|c|a
             
            //4.再继续for循环，j=2,即swap(ch,0,2)，即"cab",这个状态可以再次叫做状态A，下面的步骤同上
            /////////////-------》此时结果集为["abc","acb","bac","bca","cab","cba"]
             
            //             a|b|c(状态A)
            //               |
            //               |swap(0,2)
            //               |
            //             c|b|a(状态B)
            //             /  \
            //   swap(1,1)/    \swap(1,2)  (状态C1和状态C2)
            //           /      \
            //         c|b|a   c|a|b
             
            //5.最后退出for循环，结束。
             
            for(int j=i;j

28 数组中出现次数超过一半的数字

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

/*
这题我有两种思路
1、空间换时间
题目没有申请内存限制 可以申请一个map key存储数 value存储该数出现的字数
对数组进行遍历 如果当前数不在keys里面 直接插入 并使value为1 后面如果遇到相同的 value++
如果value>=size/2 直接返回该数
时间复杂度O(n) 空间复杂度O(n)

2、时间换空间
先对数组进行排序
如果当前数 相同数的区间
如果区间大于5 直接返回该数
由于要排序 所以 时间复杂度为O(nlogn) 
不消耗空间 所以空间复杂度为O(1)

我只写了第一种
*/

class Solution {
public:
    int MoreThanHalfNum_Solution(vector numbers) {
        if(numbers.size() == 1)return numbers[0];
        map m;
        for(int i = 0; i= numbers.size()/2)
                    return numbers[i];
                else m[numbers[i]]++;
            }else{
                m.insert({numbers[i],1});
            }
        }
        return 0;
    }
};

29 最小的K个数

输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。

/*
遇到最小的k个数 或者最大的k个数
首先要想到优先队列
最小的k个数 --->>> 最大优先队列 --->>> 大顶堆
最大的k个数 --->>> 最小优先队列 --->>> 小顶堆
所以本题 只需维护一个长为k的 最大优先队列
这就保证了当有新的数据入队后 只会优先弹出队列中最大的元素
*/
class Solution {
public:
    vector GetLeastNumbers_Solution(vector input, int k) {
        vector res;
        if(k>input.size())return res;
        
        priority_queue q; 
        for(auto x : input){
            q.push(x);
            if(q.size() > k)//只保留最小的k个数
                q.pop();
        }
        // 这k个数放到vector中
        while(!q.empty()){
            res.push_back(q.top());
            q.pop();
        }
        return res;
    }
};

30 连续子数组的最大和

HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，你会不会被他忽悠住？(子向量的长度至少是1)

/*
6,-3,-2,7,-15,1,2,2
给一个sum 表示最大和 一个max存储最大的sum
如果加sum + 当前数 <= 0 那么 sum 赋值当前数
否则 sum += 当前数
如果sum > max 
max = sum
*/
class Solution {
public:
    int FindGreatestSumOfSubArray(vector a) {
        int n = a.size(), max = INT32_MIN, sum = 0;
        if(n == 0) return 0;
        for(int i = 0; i < n; i++){
            if(sum <= 0)sum = a[i];
            else sum += a[i];
            if(max < sum)
                max = sum;
        }
        return max;
    }
};

31 整数中1出现的次数（从1到n整数中1出现的次数）

求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）

/*
首先 先算一个数中1的个数
怎么计算一个数的1？
首先先计算个位
然后右移一位
直到当前数变为0
*/

class Solution {
public:
    int NumberOf1Between1AndN_Solution(int n)
    {
        int num = 0;
        for(int i = 1; i <= n; i++)
            num += count(i);
        return num;
    }
    int count(int n){
        int res = 0;
        while(n){
            if(n % 10 == 1)
                res ++;
            n /= 10;
        }
        return res;
    }
};

32 把数组排成最小的数

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。

/*
想一下
这个相当于按两个数组合在一起 
能组合成比较小的数就是我们要想的组合
那么可以对两两进行比较
取最小的组合
并调用排序算法对数组按照组合最小的排序
排序后的数组
把所有元素合并起来的结果就是题设结果
*/

class Solution {
public:
    static bool myCompare(int &a, int &b){
        if(to_string(a) + to_string(b) < to_string(b) + to_string(a))
            return true;
        else
            return false;
    }
    string PrintMinNumber(vector numbers) {
        string str;
        if(!numbers.size())return str;
        sort(numbers.begin(),numbers.end(),myCompare);
        for(int i = 0; i < numbers.size(); i++){
            str += to_string(numbers[i]);
        }
        return str;
    }
};

33 丑数

把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。

/*
丑数只包含 2 3 5 三个质因子
那么说明 丑数S = i*2 + j*3 + k*5
所以我们维护 i j k三个变量
因为丑数是连续的 因此要保证下一个丑数和前一个丑数之间 不能含有丑数
于是在找下一个数时 分别要找 i j k对应的前一个丑数 
并取他们分别乘下一个质因子最小的数 这个数就是下一个丑数
*/
class Solution {
public:
    int GetUglyNumber_Solution(int n) {
        if(n <= 1)return n;
        vector v(1,1);
        int i = 0, j = 0, k = 0;
        long long t = 0;
        while(--n){
            t = min(v[i] * 2, min(v[j] * 3, v[k] * 5));
            if(t == v[i] * 2) i++;
            if(t == v[j] * 3) j++;
            if(t == v[k] * 5) k++;
            v.push_back(t);
        }
        return v.back();
    }
};

34  第一个只出现一次的字符

在一个字符串(0<=字符串长度<=10000，全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1（需要区分大小写）

/*
看到出现几次的字符 要想到 int chars[256] 或者 map
如果是用chars[256] 那么初始chars[256] = {0}
以后遇到每个字符 往对应的ASCII码 - 'A' ++ 到最后遍历 每个元素为1 就直接返回
使用map思路也一样一样的 如果map已经有了就++ 没有插入 最后遍历一样
*/
class Solution {
public:
    int FirstNotRepeatingChar(string str) {
        map m;
        for(int i = 0;i

35 数组中的逆序队

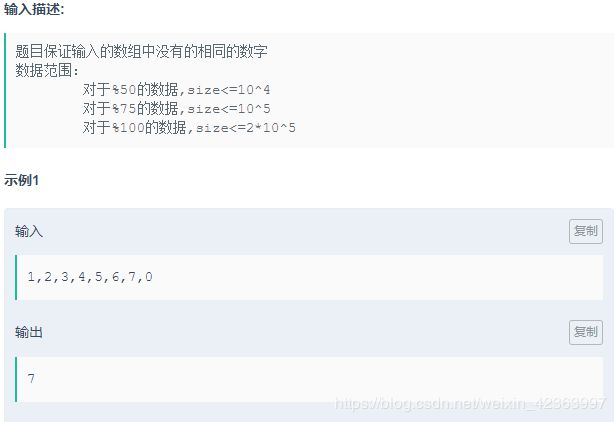
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007。

/**
本题就是考个归并排序 然后递归结束后合并数组时
如果左半边的比右半边中的数大 那么左半边所有的数和右半边这个数都构成逆序对
下面简单模拟一下归并排序 关于排序 后面会更新一个详细的 
1,2,3,4,5,6,7,0
1,2,3,4        5,6,7,0 
1,2  3,4       5,6   7,0
1 2  3 4       5 6   7 0       ans: 1
12   34        56    07        ans: 2
1234           0567            ans: 4
01234567   ans: 1 + 2 + 4 = 7
由于可能数据会很大 int32 可能会溢出 所以ans 以 long long 型
*/
class Solution {
public:
    static const int N = 1e6 + 50;
    long long ans;
    int a[N], tmp[N];//大内存申请 最好放在全局变量 由堆开辟空间
    void mergeSort(int q[], int l, int r)
    {
        if (l >= r) return;

        int mid = (l + r) >> 1;

        mergeSort(q, l, mid), mergeSort(q, mid + 1, r);

        int k = 0, i = l, j = mid + 1;
        
        while (i <= mid && j <= r)
            if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];//前一个数比后一个数小
            //后一个数比前一个数大 把前面的数对 都加到ans
            else tmp[k ++ ] = q[j ++ ],ans += mid - i + 1;
        //合并比较长的数组的那一部分
        while (i <= mid) tmp[k ++ ] = q[i ++ ];
        while (j <= r) tmp[k ++ ] = q[j ++ ];

        //把数据放到temp数组中
        for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
    }

    int InversePairs(vector nums) {
        for(int i=0;i

36 两个链表的第一个公共结点

输入两个链表，找出它们的第一个公共结点。

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};
两个链表的公共结点 其实就是两个链表的尾部一定数据相同
那么可以用两个数组分别存储两个链表的数据
然后一起从后往前遍历 当两个结点不相同时 返回上一个结点 就是第一个公共结点

举例：
1 3 5 6 7 8
  2 4 3 7 8
epoch 1: 
1 3 5 6 7
  2 4 3 7
epoch 2: 
1 3 5 6
  2 4 3
epoch 3: 
break


*/
class Solution {
public:
    ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {
        if(!pHead1 || !pHead2)return 0;
        vector v1,v2;
        auto h1 = pHead1, h2 = pHead2;
        //把两个链表数据分别装入v1 v2
        while(h1){
            v1.push_back(h1);
            h1 = h1->next;
        }
        while(h2){
            v2.push_back(h2);
            h2 = h2->next;
        }
        // 分别取到末尾
        int h1len = v1.size() - 1, h2len = v2.size() - 1;
        ListNode* res = 0; //结果指针
        //从后往前遍历
        while(h1len>=0 && h2len>=0 && v1[h1len] == v2[h2len]){
            res = v1[h1len];
            h1len--;
            h2len--;
        }
        return res;
    }
};

37 数字在排序数组中出现的次数

统计一个数字在排序数组中出现的次数。

/*
统计一个数字在排序数组中出现的次数
首先要找到这个数
那么从这个数往后遍历
累计有几个这个的数 就是结果
查找这个数用二分查找 时间复杂度可以表示O(h)=O(log2n)
一定要找这个数第一次出现的位置 所以在判断时要>=k

举例

11233367  找3  epoch1: l = 0 , r = 7 mid = 3
1123 epoch2: l = 0 , r = 3 mid = 1
23 epoch3: l = 2 , r = 3 mid = 2
3 epoch4: l = 3 , r = 3 mid = 3
3 epoch5: break l = 3 , r = 3
return l = 3
*/

class Solution {
public:
    int getFirstPos(vector &data ,int k, int l,int r){
        while(l>1;
            if(data[mid]>=k)r = mid;
            else l = mid + 1;
        }
        return l;
    }
    int GetNumberOfK(vector data ,int k) {
        int n = data.size();
        if(!n)return 0;
        
        int pos = getFirstPos(data,k,0,n - 1);
        int res = 0;
        for(int i = pos; i < n; i++){
            if(k == data[i])res++;
            else break;
        }
        return res;
    }
};

38 二叉树的深度

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};
输入一棵二叉树，求该树的深度
其实就是dfs
每往下递归一层 深度++
递归结束 更新Depth

        1
    2        3
  4    5  6    7
 8 
 中间重复的 或者包含了的 不表示了
 epoch1:  1 2 4 7   depth = 4
 epoch2:  1 2 4   depth = 3
 epoch3:  1 2 5   depth = 3
 epoch4:  1 3 6   depth = 3
 epoch4:  1 3 7   depth = 3
 所以 4 最大 返回4
*/
class Solution {
private:
    int depth = 0;
public:
    void dfs(TreeNode* r, int d){
        if(r->left) dfs(r->left, d + 1);
        if(r->right) dfs(r->right, d + 1);
        depth = max(depth, d);
    }
    int TreeDepth(TreeNode* r)
    {
        if(!r)return 0;
        dfs(r,1);
        return depth;
    }
};

39 平衡二叉树

输入一棵二叉树，判断该二叉树是否是平衡二叉树。

/**
平衡二叉树 左右子树深度差的绝对值不超过1
如果改为从下往上遍历 如果子树是平衡二叉树
则返回子树的高度 如果发现子树不是平衡二叉树
则直接停止遍历 这样至多只对每个结点访问一次
        1
    2        3
  4    5  6    7
 8 
 中间重复的 或者包含了的 不表示了
 epoch1:  1 2 3 7  结点8 return : 1 l
 epoch2:  1 2 3    结点4 return : 2 l
 epoch3:  1 2 4    结点5 return : 1 l
 epoch4:  1 2      结点2 return : 3 l
 epoch5:  1 3 5    结点6 return : 1 r
 epoch6:  1 3 6    结点7 return : 1 r
 epoch7:  1 3      结点3 return : 2 r
 epoch8:  1        结点1 return : 4 l 3 r
**/

class Solution {
public:
    
    bool IsBalanced_Solution(TreeNode* r) {
       return dfs(r) != -1;
    }
    int dfs(TreeNode* root){
        if(!root)return 0;
        int l = dfs(root->left);
        if(l<0)return -1;
        int r = dfs(root->right);
        if(r<0)return -1;
        if(abs(l-r)>1)return -1;
        return max(l,r) + 1;
    }
};

40 数组中只出现一次的数字

一个整型数组里除了两个数字之外，其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。

/*
又是找数  而且没有内存申请限制 好 上map
还是原来的 key代表数 value代表次数
遍历一次
然后遍历map 看哪个数的value为1
就存入指针就ok了
*/
class Solution {
public:
    void FindNumsAppearOnce(vector data,int* num1,int *num2) {
        map m;
        for(auto x : data){
            if(m.count(x))m[x]++;
            else m.insert({x,1});
        }
        int flag = 0;
        for(auto x: data){
            if(m[x] == 1){
                if(!flag){
                    num1[0] = x;
                    flag = 1;
                }
                else{
                    num2[0] = x;
                    break;
                } 
            }
        }
    }
};

41 和为S的连续正数序列

小明很喜欢数学,有一天他在做数学作业时,要求计算出9~16的和,他马上就写出了正确答案是100。但是他并不满足于此,他在想究竟有多少种连续的正数序列的和为100(至少包括两个数)。没多久,他就得到另一组连续正数和为100的序列:18,19,20,21,22。现在把问题交给你,你能不能也很快的找出所有和为S的连续正数序列? Good Luck!

/*
首先看看有没有内存申请限制和复杂度限制
没有 那么可以试试O(n2)
对于这题目 不管用单指针往前找 还是双指针往两边找 也是O(n2)
那么直接试试
因为题目说至少包括两个数
那么循环可以从1~n/2
每个数都自增 加入原来的数 直到超过sum
如果相等 保存序列
*/
class Solution {
public:
    vector > FindContinuousSequence(int sum) {
        vector> res;
	    for(int i = 1; i <= sum/2; i++){
		    vector v = get(i,sum);
		    if(v.size())
			    res.push_back(v);
	    }
	    return res;
    }
    vector get(int n, int sum){
        vector res,v;
        int t = 0;
        while(t < sum){
            t += n;
            res.push_back(n++);
        }
        if(t != sum) return v;
        else return res;
        
    }
};

/*
这是我之间用双指针滑动窗口写的 没有优化 所以写得比较乱
*/
import java.util.ArrayList;
public class Solution {
    public ArrayList > FindContinuousSequence(int sum) {
        ArrayList> lists = new ArrayList<>();
        int size = sum/2 + 1;
        int aa[] = new int[size];
        int temp = 0;
        for(int i =0;i list1 = new ArrayList<>();
            int cur_index = item - 1;
            int max_index = cur_index,min_index = cur_index == 0?0:cur_index-1;
            int t_sum = 0;
            while (max_index1)lists.add(list1);
                }
                max_index++;
            }
            max_index --;
            t_sum -=aa[max_index];
            max_index--;
            while (cur_index!=max_index&&t_sum0){
                t_sum += aa[min_index];
                if(t_sum == sum){
                    for(int j = aa[min_index];j<=aa[max_index];j++)list1.add(j);
                    if(!isContains(lists,list1)&&list1.size()>1)lists.add(list1);
                }
                if(t_sum>sum){
                    t_sum -= aa[max_index];
                    max_index --;
                }
                min_index --;
            }
        }
        return lists;
    }
    public boolean isContains(ArrayList> lists,ArrayList list){
        for (ArrayList a:lists) 
            if(a.get(0) == list.get(0))return true;
        return false;
    }
}

42 和为S的两个数

输入一个递增排序的数组和一个数字S，在数组中查找两个数，使得他们的和正好是S，如果有多对数字的和等于S，输出两个数的乘积最小的。

/*
看到递增 看到查找 看到两个数的和
一定想到双指针 一个指向0 一个指向末尾
从两头往中间缩小
保存乘积最小的两个数的索引
*/

class Solution {
public:
    vector FindNumbersWithSum(vector a,int sum) {
        vector res;
        if(a.size() == 0)return res;
        int l = 0, r = a.size() - 1, t = 0;
        int il = r, ir = r;
        while(l sum)r--;
            else{
                if(l * r < il * ir){
                    il = l;
                    ir = r;
                }
                l ++;
                r --;
            }
        }
        if(il != ir){
            res.push_back(a[il]);
            res.push_back(a[ir]);
        }
        return res;
    }
};

43 左旋转字符串

汇编语言中有一种移位指令叫做循环左移（ROL），现在有个简单的任务，就是用字符串模拟这个指令的运算结果。对于一个给定的字符序列S，请你把其循环左移K位后的序列输出。例如，字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果，即“XYZdefabc”。是不是很简单？OK，搞定它！

/*
这题 要么用substr 
不过 为了模拟左移
申请个队列
先把字符串放进队列
然后前n个字符出队
出队后立即入队
最后把队列中的所有字符装入string 变量
*/
class Solution {
public:
    string LeftRotateString(string str, int n) {
        queue q;
        for(auto c : str)
            q.push(c);
        while(n--){
            char c = q.front();
            q.pop();
            q.push(c);
        }
        string res;
        while(q.size()){
            res.push_back(q.front());
            q.pop();
        }
        return res;
    }
};